
HỒI QUY VÀ TƯƠNG QUAN
Là các PP toán học thường được vận dụng để nghiên
cứu các quan hệ thống kê.
1
Phân tích tương quan Phân tích hồi qui
Mục đích Đo cường độ mối quan hệ
giữa các biến Ước lượng (dự báo) giá trị
của các biến trên cơ sở giá
trị cho trước của các biến
khác
Kỹ thuật Các biến là ĐLNN và có tính
đối xứng (ryx = rxy )Biến phụ thuộc là ĐLNN
Biến độc lập là xác định
Không có tính đối xứng

PHÂN TÍCH HỒI QUY
Nghiên cứu mối quan hệ giữa một biến gọi là biến phụ
thuộc (biến được giải thích (Y)) với một hoặc một số
biến khác được gọi là biến độc lập (biến giải thích (X))
2
Các nội dung cơ bản của phân tích hồi qui
1. Xác định mức độ thay đổi của Y tương ứng với sự thay đổi của X
2. Kiểm định bản chất của sự phụ thuộc
3. Ước lượng (dự báo) giá trị biến Y tương ứng với giá trị đã biết của X
HÀM HỒI QUI TỔNG THỂ (PRF)
3
Là hàm hồi qui phản ánh mối quan hệ thực tế
giữa các biến trên phạm vi tổng thể nghiên cứu.
Ví dụ có một tổng thể gồm 30 HGĐ, thu thập dữ
liệu về chi tiêu TD (Y) và thu nhập (X) trong một
ngày, kết quả như sau:
X50 70 90 110 130 150 170 190
Y
35 41 45 71 91 99 113 133
40 49 56 90 100 115 131 145
45 63 85 94 102 131 146 147
67 88 107 149
76 151
HÀM HỒI QUI TỔNG THỂ
4
Với một cột của bảng chính là phân phối xác suất
của chi tiêu với thu nhập cho trước (P(Y/Xi)
X
50 70 90 110 130 150 170 190
P(Y/Xi)
1/3 1/4 1/5 1/3 1/4 1/3 1/3 1/5
1/3 1/4 1/5 1/3 1/4 1/3 1/3 1/5
1/3 1/4 1/5 1/3 1/4 1/3 1/3 1/5
1/4 1/5 1/4 1/5
1/5 1/5
E(Y/Xi) 40 55 70 85 100 115 130 145
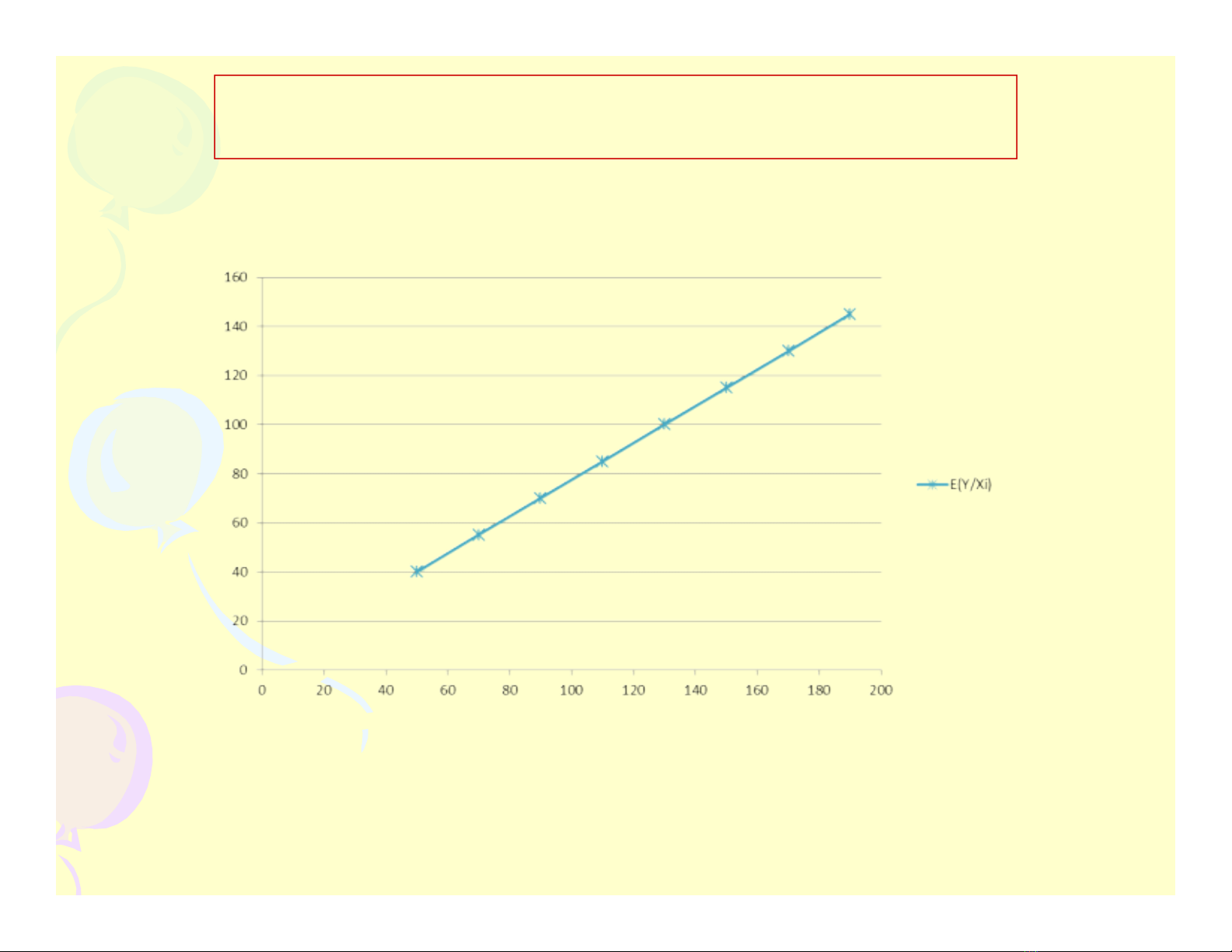
HÀM HỒI QUI TỔNG THỂ
5
E(Y/Xi) là hàm theo Xi, được mô tả: E(Y/Xi) = f(Xi)
E(Y/Xi) = f(Xi): được gọi là hàm hồi qui tổng thể.
(Cho biết giá trị trung bình của Y thay đổi như thế nào theo X)
Dạng hàm f(Xi)chưa biết, có thể tuyến tính hay phi tuyến


























