Giới thiệu tài liệu
Bài giảng Toán cao cấp 2 (Phần Giải tích): Bài 3 là một bài giảng tóm tắt về hạnh lý nhiều biến, việc phân, đạo hàm và vi phân, cực trị và ứng dụng trong kinh tế. Giáo trình viết theo một chiều rõ ràng và thống nhất, có bao gồm ví dụ và bài tập để trình bày các kiến thức chính.
Đối tượng sử dụng
Sinh viên tham khảo giáo trình Toán cao cấp 2 (Phần Giải tích): Bài 3 cho để học về hạnh lý nhiều biến, việc phân, đạo hàm và vi phân, cực trị và ứng dụng trong kinh tế.
Nội dung tóm tắt
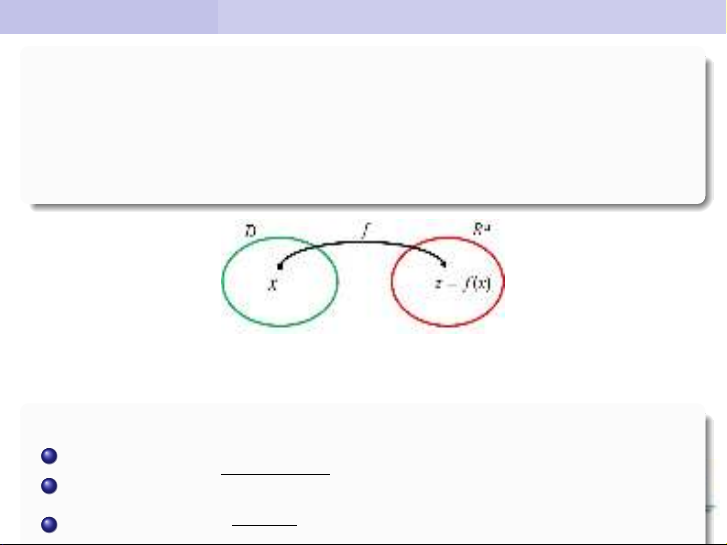
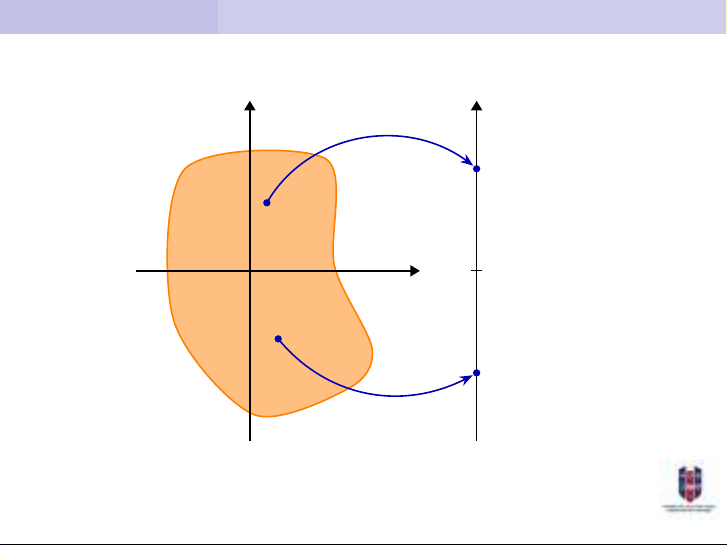
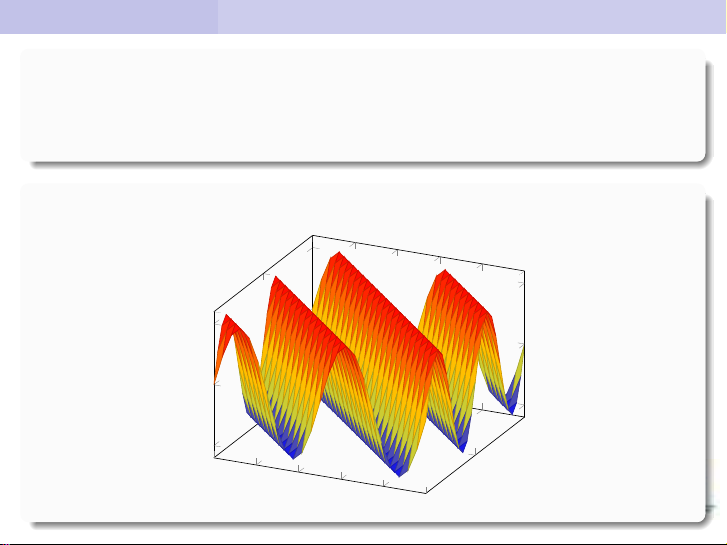
Bài giảng Toán cao cấp 2 (Phần Giải tích): Bài 3 bắt đầu với một giới thiệu về hạnh lý nhiều biến, bao gồm định nghĩa của hạnh lý và các tính chất của nó. Sau đó, chi tiết trình bày về việc phân và đạo hàm, gồm định nghĩa cho việc phân và các quy tắc để tìm kiếm việc phân. Tiếp theo là một thảo luận về cực trị, bao gồm định nghĩa cho cực trị và các quy tắc để tìm kiếm cực trị. Cuối cùng là một phần về vi phân toán hạnh lý, bao gồm định nghĩa cho vi phân toán hạnh lý và các quy tắc để tìm kiếm vi phân. Bài giảng còn gồm nhiều ví dụ và bài tập để trình bày các kiến thức và cho khả năng học tập cho học sinh. Tổng thể, bài giảng Toán cao cấp 2 (Phần Giải tích): Bài 3 là một kiến thức chính xác và khóa học lưu ý.


![Bài giảng Toán cao cấp (A2) - TS. Lê Bá Long, ThS. Đỗ Phi Nga [Chuẩn Nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250428/vihizuzen/135x160/7081745803521.jpg)




![Bài giảng Toán cao cấp 2: Bài 3 - Nguyễn Phương [CHUẨN SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250313/myhouse05/135x160/2874133_9851.jpg)
![Bài giảng Toán cao cấp 2: Bài 2 - Nguyễn Phương [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250313/myhouse05/135x160/2874132_4256.jpg)


















