ThS. ðoàn Vương Nguyên Slide bài ging Toán A3DH
Trang 1
TOÁN CAO CP A 3 ðI HC
Tài liu tham kho:
1. Giáo trình Toán cao cp A3 – Nguyn Phú Vinh – ðHCN TP. HCM.
2. Ngân hàng câu hi Toán cao cp – Nguyn Phú Vinh – ðHCN TP.HCM.
3. Gii tích hàm nhiu bin (Toán 3) – ð Công Khanh (ch biên) – NXBðHQG TP. HCM.
4. Gii tích hàm nhiu bin (Toán 4) – ð Công Khanh (ch biên) – NXBðHQG TP. HCM.
5. Phép tính Vi tích phân (tp 2) – Phan Quc Khánh – NXB Giáo dc.
6. Phép tính Gii tích hàm nhiu bin – Nguyn ðình Trí (ch biên) – NXB Giáo dc.
7. Tích phân hàm nhiu bin – Phan Văn Hp, Lê ðình Thnh – NXB KH và K thut.
8. Bài tp Gii tích (tp 2) – Nguyn Thy Thanh – NXB Giáo dc.
Chương 1. HÀM S NHIU BIN S
§1. KHÁI NIM CƠ BN
1.1. ðnh nghĩa
• Cho
2
D
⊂
ℝ
. Tương ng
:f D
→
ℝ
,
( , ) ( , )
x y z f x y
=
֏
duy nh
t,
ñư
c g
i là hàm s
2 bi
n x và y.
• T
p D
ñư
c g
i là MX
ð
c
a hàm s
và
{
}
( ) ( , ), ( , )
= ∈ = ∀ ∈ℝ
là mi
n giá tr
.
– N
u M(x, y) thì D là t
p h
p
ñ
i
m M trong
2
ℝ
sao cho
f(M) có ngh
ĩ
a, th
ư
ng là t
p liên thông. (T
p liên thông D
là t
n t
i
ñư
ng cong n
i 2
ñ
i
m b
t k
ỳ
trong D n
m hoàn
toàn trong D).
Hình a
Hình b
– N
u M(x, y) thì D là t
p h
p
ñ
i
m M trong
2
ℝ
sao cho
f(M) có ngh
ĩ
a, th
ư
ng là mi
n liên thông (n
u M, N thu
c
mi
n D mà t
n t
i 1
ñư
ng n
i M v
i N n
m hoàn toàn
trong D thì D là liên thông-Hình a)).
– Tr
tr
ư
ng h
p
2
D
=
ℝ
, D th
ư
ng
ñư
c gi
i h
n b
i 1
ñư
ng cong kín
D
∂
(biên) ho
c không. Mi
n liên thông D
là
ñơ
n liên n
u D
ñư
c gi
i h
n b
i 1
ñư
ng cong kín (Hình
a);
ñ
a liên n
u
ñư
c gi
i h
n b
i nhi
u
ñư
ng cong kín r
i
nhau t
ng
ñ
ôi m
t (Hình b).
– D là mi
n
ñ
óng n
u
M D M D
∈∂ ⇒∈
, mi
n m
n
u
M D M D
∈∂ ⇒∉
.
Chú ý
• Khi cho hàm s
f(x, y) mà không nói gì thêm thì ta hi
u
MX
ð
D là t
p t
t c
(x, y) sao cho f(x, y) có ngh
ĩ
a.
• Hàm s
n bi
n f(x
1
, x
2
,…, x
n
)
ñư
c
ñ
nh ngh
ĩ
a t
ươ
ng t
.
VD 1.
Hàm s
z = f(x, y) = x
3
y + 2xy
2
– 1 xác
ñ
nh trên
2
ℝ
.
VD 2.
Hàm s
2 2
( , ) 4
z f x y x y
= = − −
có MX
ð
là hình
tròn
ñ
óng tâm O(0; 0), bán kính R = 2.
VD 3.
Hàm s
2 2
( , ) ln(4 )
z f x y x y
= = − −
có MX
ð
là
hình tròn m
tâm O(0; 0), bán kính R = 2.
VD 4.
Hàm s
( , ) ln(2 3)
z f x y x y
= = + −
có MX
ð
là n
a
mp m
biên d: 2x + y – 3 không ch
a O(0; 0).
1.2. Gii hn ca hàm s hai bin – Hàm s liên tc
• Dãy
ñ
i
m M
n
(x
n
; y
n
) d
n
ñ
n
ñ
i
m M
0
(x
0
; y
0
) trong
2
ℝ
,
ký hi
u
0
n
M M
→
hay
0 0
( ; ) ( ; )
n n
x y x y
→
, khi
n
→ +∞
n
u
( )
2 2
0 0 0
lim , lim ( ) ( ) 0
n n n
n n
d M M x x y y
→∞ →∞
= − + − =
.
• Cho hàm s
f(x, y) xác
ñ
nh trong mi
n D (có th
không
ch
a M
0
), ta nói L là gi
i h
n c
a f(x, y) khi
ñ
i
m M(x, y)
d
n
ñ
n M
0
n
u m
i dãy
ñ
i
m M
n
(M
n
khác M
0
) thu
c D
d
n
ñ
n M
0
thì
lim ( , )
n n
n
f x y L
→∞
=
.
Ký hi
u:
0 0 0
( , ) ( , )
lim ( , ) lim ( )
x y x y M M
f x y f M L
→ →
= =
.
Nhn xét
• N
u khi
0
n
M M
→
trên 2
ñư
ng khác nhau mà dãy
{f(x
n
, y
n
)} có hai gi
i h
n khác nhau thì
0
lim ( )
M M
f M
→
∃
.
VD 5.
Cho
2
2
2 3 1
( , )
3
x y x
f x y xy
− −
=+
, tính
( , ) (1, 1)
lim ( , )
x y
f x y
→ −
.
VD 6.
Cho
2 2
( , ) xy
f x y
x y
=+
, tính
( , ) (0,0)
lim ( , )
x y
f x y
→
.
VD 7.
Cho hàm s
2 2
3
( , )
xy
f x y
x y
=+
.
Ch
ng t
( , ) (0,0)
lim ( , )
x y
f x y
→
không t
n t
i.
• Hàm s
f(x, y) xác
ñ
nh trong D ch
a M
0
, ta nói f(x, y)
liên t
!
c t
i M
0
n
u t
n t
i
0 0
( , ) ( , )
lim ( , )
x y x y
f x y
→
và
0 0
0 0
( , ) ( , )
lim ( , ) ( , )
x y x y
f x y f x y
→
=
.
• Hàm s
f(x, y) liên t
!
c trong D n
u liên t
!
c t
i m
i
ñ
i
m
M thu
c D. Hàm s
f(x, y) liên t
!
c trong mi
n
ñ
óng gi
i n
i
D thì
ñ
t giá tr
l
n nh
t và nh
nh
t trong D.
VD 8.
Xét tính liên t
!
c c
a hàm s
:
2 2
, ( , ) (0,0)
( , )
0, ( , ) (0,0)
xy x y
x y
f x y
x y
≠
+
=
=
.
ThS. ðoàn Vương Nguyên Slide bài ging Toán A3DH
Trang 2
§2. ðO HÀM RIÊNG – VI PHÂN
2.1. ðo hàm riêng
a) ðo hàm riêng cp 1
• Cho hàm s f(x, y) xác ñnh trên D cha M
0
(x
0
, y
0
). Nu
hàm s 1 bin f(x, y
0
) (y
0
là hng s) có ño hàm ti x = x
0
thì ta gi ño hàm ñó là ño hàm riêng theo bin x ca f(x,
y) ti (x
0
, y
0
).
Ký hi u:
0 0
( , )
x
f x y
hay
/
0 0
( , )
x
f x y
hay
0 0
( , )
f
x y
x
∂
∂
.
Vy
/
0 0 0 0
0 0 0
( , ) ( , )
( , ) lim
xx
f x x y f x y
f x y
x
∆ →
+ ∆ −
=∆
.
• Tương t ta có ño hàm riêng theo y ti (x
0
, y
0
) là:
/
0 0 0 0
0 0 0
( , ) ( , )
( , ) lim
yy
f x y y f x y
f x y y
∆ →
+ ∆ −
=∆
.
VD 1. Tính các ño hàm riêng ca z = x
4
– 3x
3
y
2
+ 2y
3
–
3xy ti (–1; 2).
VD 2. Tính các ño hàm riêng ca f(x, y) = x
y
(x > 0).
VD 3. Tính các ño hàm riêng ca
cos
x
z
y
=
ti
( ; 4)
π
.
• V
i hàm n bi
n ta có
ñ
nh ngh
ĩ
a t
ươ
ng t
.
VD 4.
Tính các
ñ
o hàm riêng c
a
2
( , , ) sin
x y
f x y z e z
=
.
b) ðo hàm riêng cp cao
• Các hàm s
f
x
, f
y
có các
ñ
o hàm riêng (f
x
)
x
, (f
y
)
y
, (f
x
)
y
,
(f
y
)
x
ñư
c g
i là các
ñ
o hàm riêng c
p hai c
a f.
Ký hi
u:
( )
2
2
/ /
2
x xx
xx
f f
f f f
x x x
∂ ∂ ∂
= = = =
∂ ∂ ∂
,
( )
2
2
//
2
y yy y
y
f f
f f f
y y y
∂ ∂ ∂
= = = =
∂ ∂ ∂
,
( )
2
//
x xy xy
y
f f
f f f
y x y x
∂ ∂ ∂
= = = =
∂ ∂ ∂ ∂
,
( )
2
/ /
y yx yx
x
f f
f f f
x y x y
∂ ∂ ∂
= = = =
∂ ∂ ∂ ∂
.
VD 5.
Tính các
ñ
o hàm riêng c
p hai c
a
3 2 3 4
y
z x e x y y
= + −
t
i
( 1; 1)
−
.
VD 6.
Tính các
ñ
o hàm riêng c
p hai c
a
2
( , )
x y
f x y xe
−
=
.
• Các
ñ
o hàm riêng c
p hai c
a hàm n bi
n và
ñ
o hàm
riêng c
p cao h
ơ
n
ñư
c
ñ
nh ngh
ĩ
a t
ươ
ng t
.
ðnh lý (Schwarz)
• N
u hàm s
f(x, y) có các
ñ
o hàm riêng f
xy
và f
yx
liên t
!
c
trong mi
n D thì f
xy
= f
yx
.
2.2. Vi phân
a) Vi phân cp 1
• Cho hàm s
f(x, y) xác
ñ
nh trong
2
D
⊂
ℝ
và
0 0 0
( , )
M x y D
∈
,
0 0
( , )
M x x y y D
+ ∆ + ∆ ∈
.
N
u s
gia
0 0 0 0 0 0
( , ) ( , ) ( , )
f x y f x x y y f x y
∆ = + ∆ + ∆ −
có
th
bi
u di
"
n d
ư
i d
ng:
0 0
( , ) . .
f x y A x B y x y
α β
∆ = ∆ + ∆ + ∆ + ∆
,
trong
ñ
ó A, B là nh
#
ng s
không ph
!
thu
c
,
x y
∆ ∆
và
, 0
α β
→
khi
( , ) (0,0)
x y
∆ ∆ →
, ta nói f kh
vi t
i M
0
.
• Bi
u th
c
. .
A x B y
∆ + ∆
ñư
c g
i là vi phân c
p 1 (toàn
ph
n) c
a f(x, y) t
i M
0
(x
0
, y
0
)
ng v
i
,
x y
∆ ∆
.
Ký hi
u df(x
0
, y
0
).
• Hàm s
f(x, y) kh
vi trên mi
n D n
u f(x, y) kh
vi t
i
m
i (x, y) thu
c D.
Nhn xét
• N
u f(x, y) kh
vi t
i M
0
thì f(x, y) liên t
!
c t
i M
0
.
• T
0 0
( , ) . .
f x y A x B y x y
α β
∆ = ∆ + ∆ + ∆ + ∆
, ta suy ra:
0 0 0 0
( , ) ( , ) .
f x x y f x y A x x
α
+ ∆ − = ∆ + ∆
0 0 0 0
0
( , ) ( , )
lim
x
f x x y f x y
A
x
∆ →
+ ∆ −
⇒=
∆
,
t
ươ
ng t
0 0 0 0
0
( , ) ( , )
lim
y
f x y y f x y
B
y
∆ →
+ ∆ −
=
∆
.
V
y
/ /
0 0 0 0 0 0
( , ) ( , ). ( , ).
x y
df x y f x y x f x y y
= ∆ + ∆
hay
/ /
0 0 0 0 0 0
( , ) ( , ) ( , )
x y
df x y f x y dx f x y dy
= +
.
Tng quát:
/ /
( , ) ( , ) ( , ) , ( , )
x y
df x y f x y dx f x y dy x y D
= + ∈
.
VD 7.
Tính vi phân c
p 1 c
a
2 3 5
x y
z x e xy y
−
= + −
t
i (–1; 1).
VD 8.
Tính vi phân c
p 1 c
a
2
2
( , ) sin( )
x y
f x y e xy
−
=
.
ðnh lý
• N
u hàm s
f(x, y) có các
ñ
o hàm riêng liên t
!
c t
i M
0
trong mi
n D ch
a M
0
thì f(x, y) kh
vi t
i M
0
.
b) Vi phân cp cao
• Vi phân c
p 2:
(
)
2 2
2
/ / 2 // / / 2
( , ) ( , )
( , ) 2 ( , ) ( , )
xy
x y
d f x y d df x y
f x y dx f x y dxdy f x y dy
=
= + +
.
• Vi phân c
p n:
( )
1 ( )
0
( , ) ( , ) ( , )
k n k
n
n n k n k n k
nx y
k
d f x y d df x y C f x y dx dy
−
− −
=
= =
∑
.
ThS. ðoàn Vương Nguyên Slide bài ging Toán A3DH
Trang 3
VD 9. Tính vi phân cp 2 ca
2 3 2 3 5
( , ) 3
f x y x y xy x y
= + −
ti (2; –1).
VD 10. Tính vi phân cp 2 ca
2
( , ) ln( )
f x y xy
=.
c) ng dng vi phân cp 1 vào tính gn ñúng giá tr hàm
s
0 0
/ /
0 0 0 0 0 0
( , )
( , ) ( , ). ( , ).
x y
f x x y y
f x y f x y x f x y y
+ ∆ + ∆ ≈
≈ + ∆ + ∆
.
VD 11. Tính gn ñúng
1,02
0,97
arctg
.
2.3. ðo hàm ca hàm s hp
• Cho hàm s f(u, v), trong ñó u = u(x) và v = v(x) là nh#ng
hàm s ca x. Nu f(u, v) kh vi ca u, v và u(x), v(x) kh
vi ca x thì
/ /
. .
u v
df du dv
f f
dx dx dx
= +
. Vi
, ,
df du dv
dx dx dx
là các
ño hàm toàn phn theo x.
• Nu hàm s f(x, y) kh vi ca x, y và y = y(x) là hàm s
kh vi ca x thì
/ /
.
x y
df dy
f f
dx dx
= +
.
VD 12. Cho
2 2
2 , , sin
x
z u uv v u e v x
−
= − + = =
. Tính
dz
dx
.
VD 13. Cho
2 2 2
( , ) ln( ), sin
f x y x y y x
= + =
. Tính
df
dx
.
2.4. ðo hàm ca hàm s n
• Cho hai bin x, y tha phương trình F(x, y) = 0 (*).
Nu y = y(x) là hàm s xác ñnh trong 1 khong nào ñó sao
cho khi th y(x) vào (*) ta ñưc ñng nht thc thì y = y(x)
là hàm s n xác ñnh bi (*).
VD 14.
Xác ñnh hàm s $n y(x) trong phương trình x
2
+ y
2
– 4 = 0.
• ðo hàm hai v (*) theo x, ta ñưc:
/
/ / /
/
( , )
( , ) ( , ). 0 , ( , ) 0
( , )
x
x y y
y
F x y
F x y F x y y y F x y
F x y
′ ′
+ =
⇒
= − ≠
.
VD 15. Cho
0
x y
xy e e
− + =
. Tính
y
′
.
VD 16. Cho
3 2 4
( 1) 0
y x y x
+ + + =
. Tính
y
′
.
VD 17. Cho
2 2
ln
y
x y arctg
x
+ =
. Tính
y
′
.
• Cho hàm s $n hai bin z = f(x, y) xác ñnh bi
F(x, y, z)) = 0, vi
/
( , , ) 0
z
F x y z
≠
ta có:
/ / /
/
/
/
/ / /
/
/
/
( , , ) ( , , ). ( , ) 0
( , , )
( , ) ,
( , , )
( , , ) ( , , ). ( , ) 0
( , , )
( , ) .
( , , )
x z x
x
x
z
y z y
y
y
z
F x y z F x y z z x y
F x y z
z x y
F x y z
F x y z F x y z z x y
F x y z
z x y
F x y z
• + =
⇒= −
• + =
⇒= −
VD 18. Cho
cos( )
xyz x y z
= + +
. Tính
/ /
,
x y
z z
.
§3. CC TR C A HÀM HAI BIN S
3.1. ðnh nghĩa
• Hàm s
z = f(x, y)
ñ
t c
c tr
(
ñ
a ph
ươ
ng) t
i
ñ
i
m
M
0
(x
0
; y
0
) n
u v
i m
i
ñ
i
m M(x, y) khá g
n nh
ư
ng khác
M
0
thì hi
u f(M) – f(M
0
) có d
u không
ñ%
i.
• N
u f(M) – f(M
0
) > 0 thì f(M
0
) là c
c ti
u và M
0
là
ñ
i
m
c
c ti
u; f(M) – f(M
0
) < 0 thì f(M
0
) là c
c
ñ
i và M
0
là
ñ
i
m
c
c
ñ
i. C
c
ñ
i và c
c ti
u g
i chung là c
c tr
.
VD 1.
Hàm s
f(x, y) = x
2
+ y
2
– xy
ñ
t c
c ti
u t
i O(0; 0).
3.2. ðnh lý
a) ði!u kin cn
• N
u hàm s
z = f(x, y)
ñ
t c
c tr
t
i M
0
(x
0
, y
0
) và t
i
ñ
ó
hàm s
có
ñ
o hàm riêng thì:
/ /
0 0 0 0
( , ) ( , ) 0
x y
f x y f x y
= =
.
Chú ý.
ð
i
m M
0
th
a
/ /
0 0 0 0
( , ) ( , ) 0
x y
f x y f x y
= =
ñư
c g
i
là
ñ
i
m d
ng, có th
không là
ñ
i
m c
c tr
c
a z.
b) ði!u kin ñ.
Gi
s
f(x, y) có
ñ
i
m d
ng là M
0
và có
ñ
o hàm riêng c
p hai t
i lân c
n
ñ
i
m M
0
.
ð
t
2 2
/ / / / / /
0 0 0 0 0 0
( , ), ( , ), ( , )
xy
x y
A f x y B f x y C f x y
= = =
.
Khi
ñ
ó:
+ N
u AC – B
2
> 0 và A > 0 thì hàm s
ñ
t c
c ti
u t
i
ñ
i
m M
0
;
AC – B
2
> 0 và A < 0 thì hàm s
ñ
t c
c
ñ
i t
i
ñ
i
m M
0
.
+ N
u AC – B
2
< 0 thì hàm s
không có c
c tr
(
ñ
i
m M
0
ñư
c g
i là
ñ
i
m yên ng
a).
+ N
u AC – B
2
= 0 thì ch
ư
a th
k
t lu
n hàm s
có c
c tr
hay không (dùng
ñ
nh ngh
ĩ
a
ñ
xét).
3.3. C"c tr t" do
Cho hàm s
z = f(x, y).
ð
tìm c
c tr
c
a f(x, y) trên MX
ð
D, ta th
c hi
n các b
ư
c sau:
B
ư
c 1. Tìm
ñ
i
m d
ng M
0
(x
0
; y
0
) b
ng cách gi
i h
:
/
0 0
/
0 0
( , ) 0
( , ) 0
x
y
f x y
f x y
=
=
.
B
ư
c 2. Tính
2
/ / / /
0 0 0 0
( , ), ( , )
xy
x
A f x y B f x y
= =
,
2
/ / 2
0 0
( , )
y
C f x y AC B
=⇒∆ = −
.
B
ư
c 3.
+ N
u
∆
> 0 và A > 0 thì k
t lu
n hàm s
ñ
t c
c ti
u t
i
M
0
và c
c ti
u là f(M
0
);
+ N
u
∆
> 0 và A < 0 thì k
t lu
n hàm s
ñ
t c
c
ñ
i t
i
M
0
và c
c
ñ
i là f(M
0
).
+ N
u
∆
< 0 thì k
t lu
n hàm s
không
ñ
t c
c tr
.
+ N
u
∆
= 0 thì không th
k
t lu
n (trong ch
ươ
ng trình h
n
ch
lo
i này).
VD 2.
Tìm
ñ
i
m d
ng c
a hàm s
z = xy(1 – x – y).
VD 3.
Tìm c
c tr
c
a hàm s
z = x
2
+ y
2
+ 4x – 2y + 8.
VD 4.
Tìm c
c tr
c
a hàm s
z = x
3
+ y
3
– 3xy – 2.
VD 5.
Tìm c
c tr
c
a hàm s
z = 3x
2
y + y
3
– 3x
2
– 3y
2
+ 2.
ThS. ðoàn Vương Nguyên Slide bài ging Toán A3DH
Trang 4
3.4. C"c tr có ñi!u kin
• Cho hàm s z = f(x, y) xác ñnh trên lân cn ca ñim
M
0
(x
0
; y
0
) thuc ñưng cong
( , ) 0
x y
ϕ
=
. N
u t
i
ñ
i
m M
0
hàm s
f(x, y)
ñ
t c
c tr
thì ta nói
ñ
i
m M
0
là
ñ
i
m c
c tr
c
a f(x, y) v
i
ñ
i
u ki
n
( , ) 0
x y
ϕ
=
.
•
ð
tìm c
c tr
có
ñ
i
u ki
n c
a hàm s
f(x, y) ta dùng
phương pháp kh
ho
c
nhân t Lagrange
.
Phương pháp kh#
T
ph
ươ
ng trình
( , ) 0
x y
ϕ
=
, ta rút x ho
c y th
vào f(x, y)
và tìm c
c tr
hàm 1 bi
n.
VD 6.
Tìm c
c tr
c
a hàm s
f(x, y) = x
2
+ y
2
– xy + x + y
v
i
ñ
i
u ki
n x + y + 3 = 0.
VD 7.
Tìm c
c tr
c
a hàm s
f(x, y) = xy v
i
ñ
i
u ki
n:
2x + 3y – 5 = 0.
Phương pháp nhân t# Lagrange
Bưc 1
. L
p hàm Lagrange:
( , , ) ( , ) ( , )
L x y f x y x y
λ λϕ
= +
,
λ
là nhân t
Lagrange.
Bưc 2.
Gi
i h
:
'
'
'
0
0
0
x
y
L
L
L
λ
=
=⇒
=
ñ
i
m d
ng M
0
(x
0
; y
0
)
ng v
i
λ
0
.
Bưc 3
Tính
2
0 0
( , )
d L x y
2 2
'' 2 '' '' 2
0 0 0 0 0 0
( , ) 2 ( , ) ( , )
xy
x y
L x y dx L x y dxdy L x y dy
= + +
.
ðiu kin ràng buc:
/ /
0 0 0 0 0 0
( , ) 0 ( , ) ( , ) 0
x y
d x y x y dx x y dy
ϕ ϕ ϕ
=⇒+ =
(1)
và
(dx)
2
+ (dy)
2
> 0 (2).
Bưc 4
T
ñ
i
u ki
n (1) và (2), ta có:
+ N
u
2
0 0
( , ) 0
d L x y
>
thì hàm s
ñ
t c
c ti
u t
i M
0
.
+ N
u
2
0 0
( , ) 0
d L x y
<
thì hàm s
ñ
t c
c
ñ
i t
i M
0
.
+ N
u
2
0 0
( , ) 0
d L x y
=
thì
ñ
i
m M
0
không là
ñ
i
m c
c tr
.
VD 9.
Tìm c
c tr
c
a hàm s
z = 2x + y v
i
ñ
i
u ki
n x
2
+ y
2
= 5.
VD 10.
Tìm c
c tr
c
a hàm s
z = xy v
i
ñ
i
u ki
n
2 2
1
8 2
x y
+ =
.
Chương 2. TÍCH PHÂN B$I
§1. TÍCH PHÂN B$I HAI (KÉP)
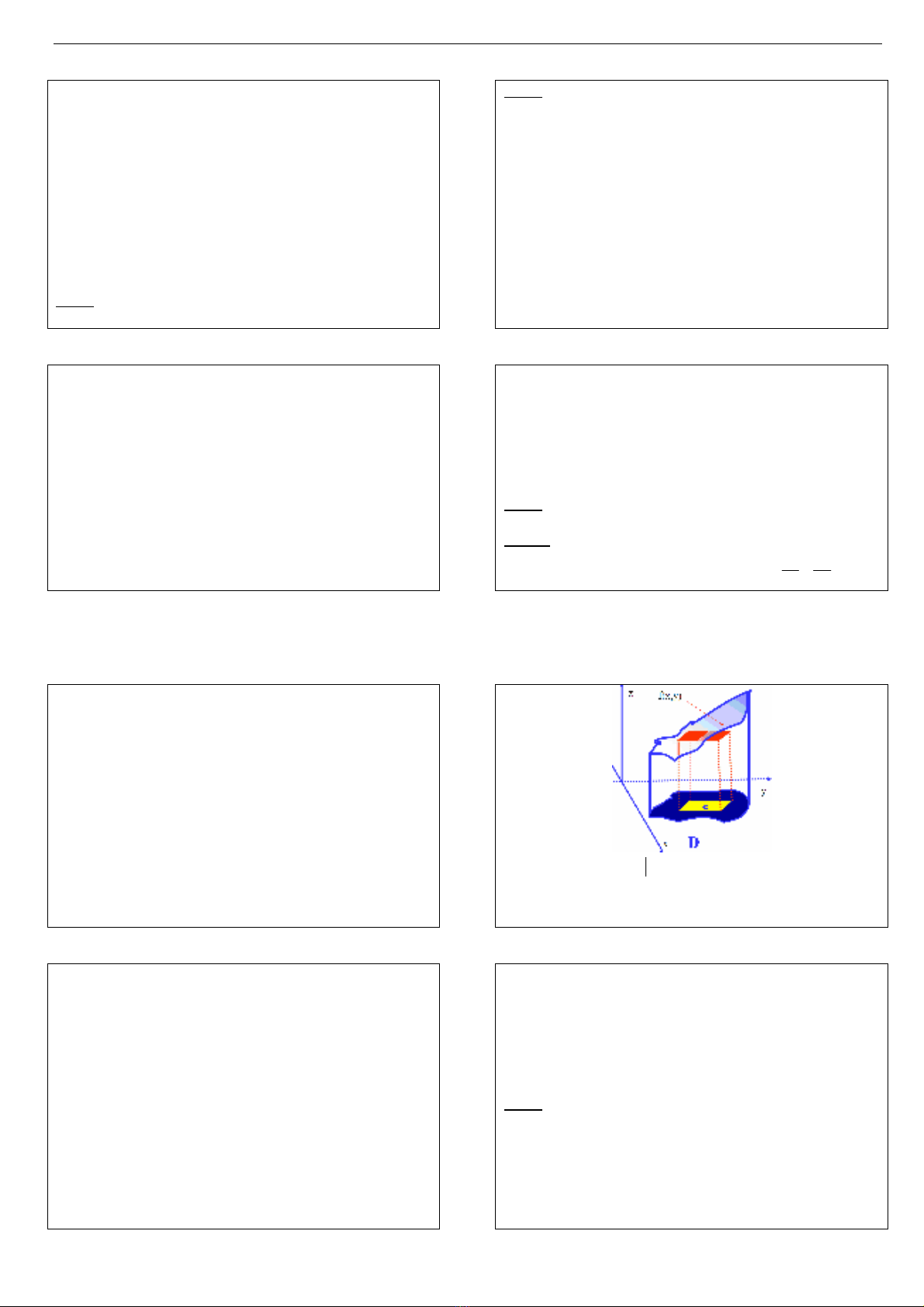
1.1. Bài toán m% ñu (th& tích khi tr cong)
• Xét hàm s
z = f(x, y) liên t
!
c, không âm và m
t m
t tr
!
có các
ñư
ng sinh song song Oz,
ñ
áy là mi
n ph
'
ng
ñ
óng D
trong Oxy.
ð
tính th
tích kh
i tr
!
, ta chia mi
n D thành n ph
n không
d
(
m lên nhau, di
n tích m
)
i ph
n là
∆
S
i
(i=1,2,…,n). Nh
ư
v
y kh
i tr
!
cong
ñư
c chia thành n kh
i tr
!
nh
. Trong
m
)
i
∆
S
i
ta l
y
ñ
i
m M
i
(x
i
; y
i
) tùy ý. Ta có th
tích
∆
V
i
c
a
kh
i tr
!
nh
là:
1
( ; ) ( , )
n
i i i i i i i
i
V f x y S V f x y S
=
∆ ≈ ∆ ⇒≈ ∆
∑
.
G
i
{
}
max ( , ) ,
i i
d d A B A B S
= ∈∆
là
ñưng kính
c
a
i
S
∆
.
Ta có:
max 0 1
lim ( , )
i
n
i i i
di
V f x y S
→=
= ∆
∑
.
1.2. ðnh nghĩa
• Cho hàm s
z = f(x, y) xác
ñ
nh trên mi
n
ñ
óng gi
i n
i,
ñ
o
ñư
c D trong Oxy. Chia mi
n D m
t cách tùy ý thành n
ph
n không d
(
m lên nhau, di
n tích m
)
i ph
n là
∆
S
i
(i=1,2,…,n). Trong m
)
i
∆
S
i
ta l
y
ñ
i
m M
i
(x
i
; y
i
) tùy ý. Khi
ñ
ó
1
( , )
n
n i i i
i
I f x y S
=
= ∆
∑
ñư
c g
i là
tng tích phân
c
a hàm
f(x, y) trên D (
ng v
i phân ho
ch
∆
S
i
và các
ñ
i
m M
i
).
N
u
max 0 1
lim ( , )
i
n
i i i
di
I f x y S
→=
= ∆
∑
t
n t
i h
#
u h
n, không ph
!
thu
c vào phân ho
ch
∆
S
i
và cách ch
n
ñ
i
m M
i
thì s
I
ñư
c g
i là
tích phân bi hai
c
a f(x, y) trên D.
Ký hi
u
( , )
D
I f x y dS
=
∫∫
.
ðnh lý.
Hàm f(x, y) liên t
!
c trong mi
n b
ch
n,
ñ
óng D thì
kh
tích trong D.
• N
u t
n t
i tích phân, ta nói f(x, y) kh
tích; f(x, y) là hàm
d
ư
i d
u tích phân; x, y là các bi
n tích phân.
Chú ý
1) N
u chia D b
i các
ñư
ng th
'
ng song song v
i các tr
!
c
t
a
ñ
thì
∆
S
i
=
∆
x
i
.
∆
y
i
hay dS = dxdy.
V
y
( , ) ( , )
D D
I f x y dS f x y dxdy
= =
∫∫ ∫∫
.
2)
( , ) ( , )
D D
f x y dxdy f u v dudv
=
∫∫ ∫∫
.
ThS. ðoàn Vương Nguyên Slide bài ging Toán A3DH
Trang 5
Nhn xét
1)
( )
D
dxdy S D
=
∫∫
(di n tích min D).
2) f(x, y) > 0, liên t!c ∀(x, y) ∈ D thì
( , )
D
f x y dxdy
∫∫
là th
tích hình tr! có các ñưng sinh song song vi Oz, hai ñáy
gii hn bi các mt z = 0 và z = f(x, y).
1.3. Tính cht ca tích phân kép
• Tính cht 1. Hàm s f(x, y) liên t!c trên D thì f(x, y) kh
tích trên D.
• Tính cht 2. Tính tuyn tính:
[ ( , ) ( , )]
D D D
f x y g x y dxdy fdxdy gdxdy
± = ±
∫∫ ∫∫ ∫∫
;
( , ) ( , ) ,
D D
kf x y dxdy k f x y dxdy k
= ∈
∫∫ ∫∫
ℝ
.
• Tính cht 3
Nu chia D thành D
1
và D
2
bi ñưng cong có di n tích
bng 0 thì:
1 2
( , ) ( , ) ( , )
D D D
f x y dxdy f x y dxdy f x y dxdy
= +
∫∫ ∫∫ ∫∫
.
1.4. Phương pháp tính tích phân kép
1.4.1. ðưa v! tích phân l'p
ðnh lý (Fubini)
• Gi s tích phân
( , )
D
f x y dxdy
∫∫
tn ti, vi
1 2
{( , ) : , ( ) ( )}
D x y a x b y x y y x
= ≤ ≤ ≤ ≤
và vi m)i
[ , ]
x a b
∈
c ñnh
2
1
( )
( )
( , )
y x
y x
f x y dy
∫
tn ti thì:
2 2
1 1
( ) ( )
( ) ( )
( , ) ( , ) ( , )
y x y x
b b
D a y x a y x
f x y dxdy f x y dy dx dx f x y dy
= =
∫∫ ∫ ∫ ∫ ∫
.
Tương t,
1 2
{( , ) : ( ) ( ), }
D x y x y x x y c y d
= ≤ ≤ ≤ ≤
thì:
2 2
1 1
( ) ( )
( ) ( )
( , ) ( , ) ( , )
x y x y
d d
D c x y c x y
f x y dxdy f x y dx dy dy f x y dx
= =
∫∫ ∫ ∫ ∫ ∫
.
Chú ý
1) Khi
{( , ) : , } [ , ] [ , ]
D x y a x b c y d a b c d
= ≤ ≤ ≤ ≤ = ×
(hình ch#
nh
t) thì:
( , ) ( , ) ( , )
b d d b
D a c c a
f x y dxdy dx f x y dy dy f x y dx
= =
∫∫ ∫ ∫ ∫ ∫
(hoán v
c
n).
2)
1 2
{( , ) : , ( ) ( )}
D x y a x b y x y y x
= ≤ ≤ ≤ ≤
và
f(x, y) = u(x).v(y) thì:
2
1
( )
( )
( , ) ( ) ( )
y x
b
D a y x
f x y dxdy u x dx v y dy
=
∫∫ ∫ ∫
.
T
ươ
ng t
,
1 2
{( , ) : ( ) ( ), }
D x y x y x x y c y d
= ≤ ≤ ≤ ≤
thì:
2
1
( )
( )
( , ) ( ) ( )
x y
d
D c x y
f x y dxdy v y dy u x dx
=
∫∫ ∫ ∫
.
3) N
u D là mi
n ph
c t
p thì ta chia D ra thành nh
#
ng
mi
n
ñơ
n gi
n nh
ư
trên.
VD 1.
Xác
ñ
nh c
n
tích phân l
p khi tính tích phân
( , )
D
I f x y dxdy
=
∫∫
trong các tr
ư
ng h
p sau:
1) D gi
i h
n b
i các
ñư
ng y = 0, y = x và x = a.
2) D gi
i h
n b
i các
ñư
ng y = 0, y = x
2
và x + y = 2.
VD 2.
Tính
D
I xydxdy
=
∫∫
v
i D gi
i h
n b
i y = x – 4, y
2
= 2x.
ði th( t" ly tích phân
2
1
( )
( )
( , )
y x
b
a y x
I dx f x y dy
=
∫ ∫
2
1
( )
( )
( , )
x y
d
c x y
I dy f x y dx
=
∫ ∫