
Giảng viên Vũ Đỗ Huy Cường
VI TÍCH PHÂN
HÀM SỐ MỘT BIẾN
Giảng viên
Vũ Đỗ Huy Cường
Khoa Toán-Tin học
Đại học Khoa học Tự nhiên
vdhuycuong@gmail.com
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 1 / 148

Giảng viên Vũ Đỗ Huy Cường
Mục lục
1Hàm số và tính chất
Khái niệm hàm số
Tính chất cơ bản của hàm số
2Giới hạn và Liên tục
Giới hạn của hàm số
Tính liên tục của hàm số
3Đạo hàm và các ứng dụng
Các quy tắc của đạo hàm
Đạo hàm hàm chuõi
Ý nghĩa hình học
Ứng dụng của đạo hàm
4Tích phân và các ứng dụng
Nguyên hàm của hàm số
Tích phân xác định
Tích phân suy rộng
Ứng dụng của tích phân
5Dãy số và chuỗi số
Dãy số và các phép tính
Chuỗi số và các phép tính
Chuỗi hàm và các phép tính
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 2 / 148

Giảng viên Vũ Đỗ Huy Cường
Chương 1
Hàm số thực
và
các tính chất cơ bản
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 3 / 148
Giảng viên Vũ Đỗ Huy Cường
1.1. Hàm số và tính chất
1.1.1. Định nghĩa hàm số
Hầu hết các tính toán đều dựa trên tập số thực. Số thực là các số
có thể được biểu diễn dưới dạng thập phân như
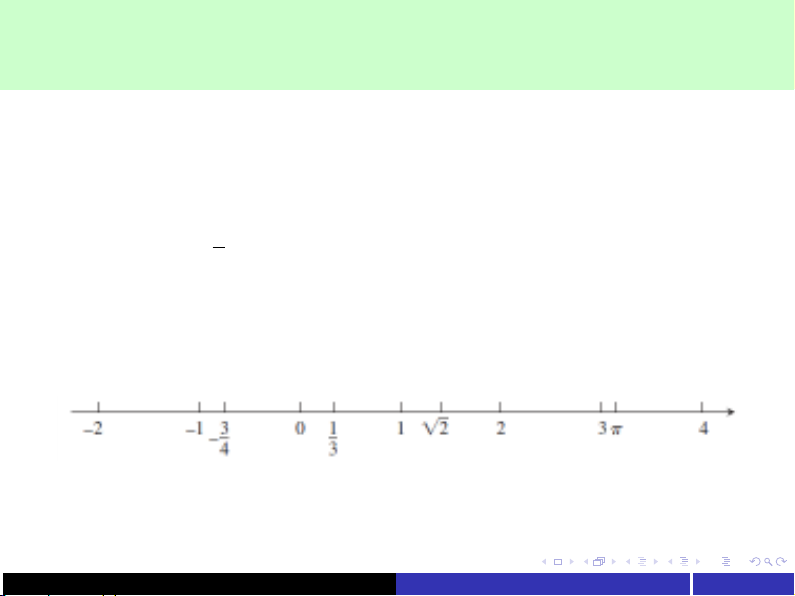
−3/4=−0.75000...
1/3=0.33333...
√2=1.4142...
Các số thực có thể được biểu diễn như các điểm trên một trục số
gọi là trục số thực.
Kí hiệu IR được dùng để chỉ tập số thực và trục số thực.
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 4 / 148
Giảng viên Vũ Đỗ Huy Cường
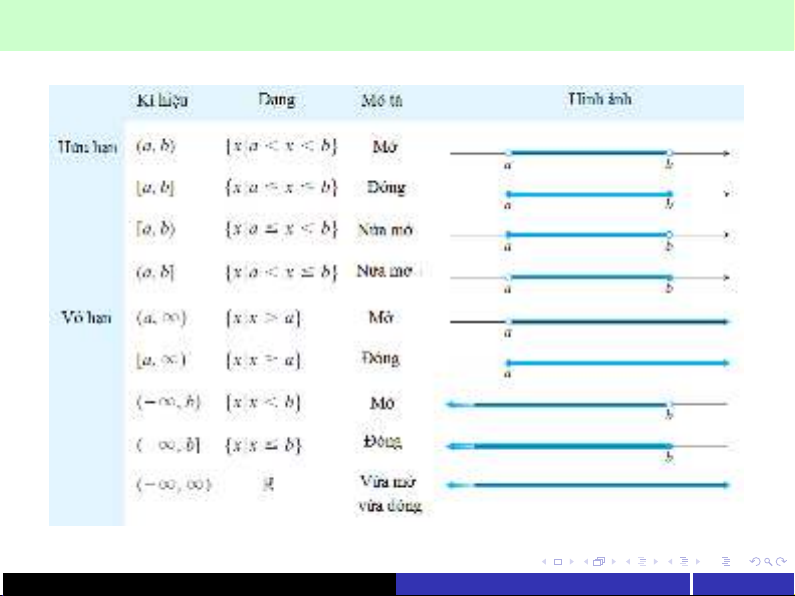
1.1.1. Định nghĩa hàm số
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 5 / 148


























