!"ω#ϕ
$" $
%
!"ω#ϕ
%
$"%$
&'()*+,-!
$ϕ
.ϕ
%
%/π0 /12!345
6$ϕ
.ϕ
%
"%/# $π5
$ϕ
.ϕ
%
"%/# $
2
π
5
($ϕ
.ϕ
%
7'6/8
9:;06<,()*27
-=7>12-6(?3)@
AB07C/D6<+8E7062B-27
12!8
$Fϕ
ϕ
%
#%/πA2" $7
!"ω#ϕ
$
!"ω#ϕ
%
#%/π$
!"ω#ϕ
%
$0
%
!"ω#ϕ
%
$
FG7
21
a
y
a
x=
x
a
a
y
1
2
=
H.
≤
!"
ω
#
ϕ
$
≤
4.
≤
≤
HB-I$24J6(?6K
x
a
a
y
1
2
=
AL .
≤
≤
6$92M-I$
!"
ω
#
ϕ
$
!"
ω
#
ϕ
%
#%/
π
#
π
$.
!"
ω
#
ϕ
%
$
FG7N4J6(?6K
x
a
a
y
1
2
−=
AL .
≤
≤
$F
ϕ
ϕ
%
#"%/# $
2
π
(?(2N6>
1
a
y
a
x
2
2
2
2
1
2
=+
26(?+41O-AP071LA2Q;
48
($=/D-" $A2"%$8R3</2!3!
" $A2"%$
11
1
sin.sincos.cos
ϕωϕω
tt
a
x−=
"S$
22
2
tt
a
y
ϕωϕω
sin.sincos.cos
−=
"T$
UV"S$AL!
ϕ%
A2"T$AL.!
ϕ
WA<ALA<
)sin(.sincoscos
121
2
2
1
t
a
y
a
x
ϕϕωϕϕ
−=−
"X$
9V"S$AL!
ϕ
%
A2"T$AL.!
ϕ
WA<ALA<
)sin(cossinsin
121
2
2
1
t
a
y
a
x
ϕϕωϕϕ
−=−
"Y$
Z-"X$A2"Y$WA<ALA<
)(sin)cos(
12
2
12
21
2
2
2
2
1
2
aa
xy2
a
y
a
x
ϕϕϕϕ
−=−−+
"[$
"[$6(?+41O-8
!"!#$%#$#%&!'
ϕ
(
)
ϕ
*
%&+,-./012#3
RPPG\]<\ZALAB3A
T^/_+W1G\
ZKA\]ALAB3A
%
S^/_+8
FAB36PP4+A]Z0Z]7`
a)C+]Z6;!8F!bOAB36cP>
0'45.4++!5+6
4+45.6
=v
F,
./, sm539
vv
vv2
v
1
v
1
2
v
s
v
s
ss
tt
ss
v
21
21
2121
=
+
=
+
=
+
+
=
+
+
=
A(
F!3,
./,
sm539v =
R+>R+J/=X^+
PP5/PPd
%^^ + 6e I
+ a- PP "f .%$8 Z< PP
ALAB3SY/_+8
fQ $ U+ -= c
L 2 a- N PP` Z< ;
+ALAB3A
%
^0g/_+5
6$U+-=ALAB 3Q
6;647a-,PP`
$R3a-NPPZ++GRLZ-=6;+
PPG]LZ
12
v
AB
v
MB =
" $
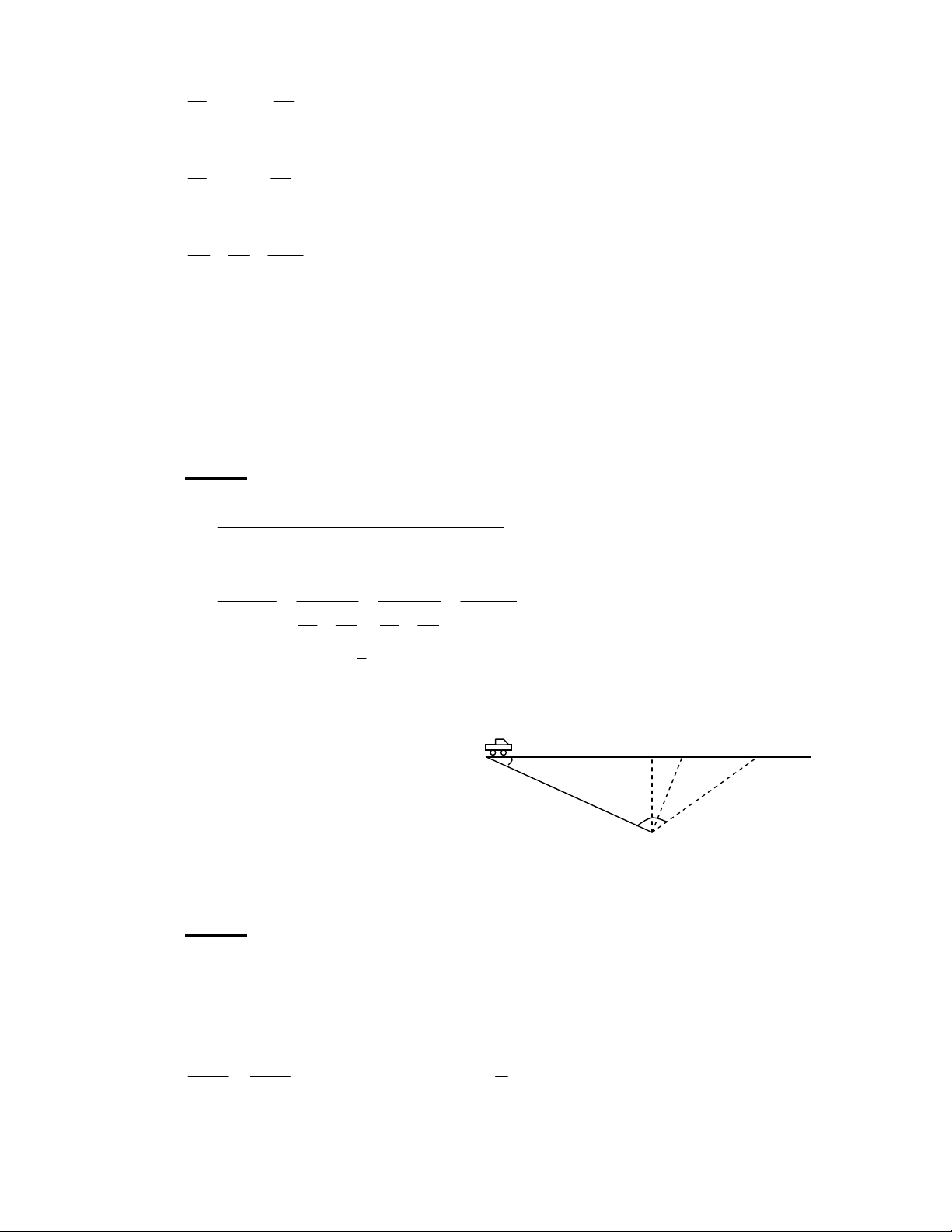
hD('1:2!3!]ZR7
,
sinsin
αβ
ABMB =
AL
a
h
=
β
sin
"%$
FG" $A2"%$N
]
R
Z
β
α
if E
f
.
%

8330
v
v
a
h
2
1
,.sin ==
α
α
XY
^
S^ja
α
%S
^
S^j8
775+0''89:;<0
α
=>:;?<.
'
'
30
123
30
56
00
≤≤
α
3@+
'
'
30
123
30
56
00
<<
α
5+0''
5?++8<AB3
C/'+?DE5+'+<F?<.+G0'
2
1
v
v
a
h.sin >
α
3
:0
MD
v
v
AD
h
a
v
v
a
h
MD
1
AD
ADMD
2
1
2
1
.....
sin
.sin
sinsin =
>=→=
β
α
αβ
8
21
v
MD
v
AD >
1-05++!8'F95++!5+'F#3
6$7a-,PPALAB3Qk2;1N2+
<+l121NcPPL"+a-NPP2/P-=+,1C-O
+$0AAB0c-I$@LA2AB3+-=7)
2
1
v
v
a
h.sin =
α
HALm
α
!"
α
$
≤
4
12
2
1
v
a
h
v1
v
v
a
h.. ≥
≤
h
hkm9sm52
a
hv
v
1
2
//,
min
===
8
9N20+-=cLRi0ALRi
⊥
]R8
RAB,=G/OI6KS^^8fQ!61V
ABLa0<
$nOI614"cLJ>$ALAB3X_!5
6$nOI3"c-J>$ALAB3X_!5
$nOI>48
n/OI0ABK4/OIcAB3/OI8U</O
I 3(LALAB3A
^
+2ABL=C
-6B+
htg
2
1
tv
2
0
=+ ..
8
om(-27/<)=
g
vgh2v
t
0
2
0
−+
=
8
n/OI14403(La>40-(6>
2ALAB36IA
^
.X_!0A
^
X_!5aA
^
^A27/<)=
$g0T!5 6$[0S!5 $[0g!8
RAB,=Gf#c-J>EEj"Ep12V
f#$8oq1N7AB>,r14GEpc-J>
ALAB3A
^
8
$fQAB3A
^
-=6;64ABa-K`

6$FO/=@ABL1Na-c+`
$U</P7AB>AB>1L6;64`
oIL1P>M(
$ F+ AB G E< a- 12
g
H2
t=
l
6;+AB%GEj<s0(7
gH2
H
2
hH
2
gt
t
h
vtg
2
1
tvh
0
2
0
+
=+=→−=
..
6$n=@AB+L/a-,
Oc)C+!A2!jAB,
"f#$."!#!j$8
( ) ( )
).(
...
tgH2H2
H
2
hH
tvhHtg
2
1
tvgt
2
1
hHx
0
2
0
2
−
+
=
−+=
−−−+=
$ hD ( P > ) A0 0 ! J 6< t
sa2vv
2
0
2
..=−
ALAB3KM6;A^0.0!
!0</P
7!M=KAB 0AB%14<M12
H4
hH
g2
v
h
22
)(
max
+
==
8
F=M(ABG u0Yr8FO
$vC+2AB,^0 VIA2^0 V3+
8
6$F+I<AB< IA2 38
hD(P>A)C+AB,!+/G1N6eI
,=
2
gt
2
1
s=
!b7P>)cA+AB,
+7/GA'O=12
g
h2
t=
8-(P>2!b=1+
,VQ62B-2
$vC+2AB,^0 !I
m04901089
2
1
tg
2
1
s
22
1
,,.,. ===
8
Ft+AB
( )
s2
89
6192
g
h2
t=== ,
,.
8
vC+AB,^0 !3q0,Oc)C+,
%.^0 0u!I
( ) ( ) ( )
m9110289
2
1
61910tg
2
1
hs
22
2
,,.,.,, =−−=−−=
8
f
E
Ej
s

6$FM4
F+AB, I
s450
89
12
g
s2
t
3
3
,
,
.===
8
F+AB< 3
s050
89
6182
2ttt
4
,
,
,. =−=−=
H"(I$J<
6
FG6]0Z0o4Add+W+=6AB8HB
>c-J>]R)VAdd"f .S$0AB>c(V
ZR0AB>6c(VoR8fQAB2LRL40<6Q)!`
vC+A23AB> !
%w0
0AB>!
%
%w!
^
AMB
0
%
!
^
AMB
0AB>6!
S
%w!
^
AMB
0
S
!
^
AMC
8
UB0+<RAB12
3
3
32
2
2
1
1
1
a
s2
tt
a
s2
g
R4
a
s2
t======
HB06ABqLR1N8
=rABc-J>GT^ALAB3A
^
6;647La
$FL
τ
V!AL+,-ABM(`
6$h
τ
V!AL+,-ABM(`
9 ^_!
%
8
hD(P>O+</62X
g
vgh2v
t
0
2
0
−+
=
A2P>+M(
g
h2
t=
AB !L0 -= r AB 3 (L AL AB 3 A
^
= C
-
( )
gh2vggh2v
g
vgh2v
g
h2
0
2
0
0
2
0+−=+→=
−+
−
ττ
]
Z
o
R
f
.
S


























