Bài s 2ố
Cho m t c c u robot 2DOF nh hình vộ ơ ấ ư ẽ
S d ng matlab- Simulinkử ụ
1. Xây d ng mô hình toán h c robotự ọ
2. Thi t k b đi u khi n PID bù tr ng tr ng. Ch y mô ph ngế ế ộ ề ể ọ ườ ạ ỏ
S li u c a robot:ố ệ ủ
Chi u dài thanh n i 1: lề ố 1 = 0,5 m
Chi u dài thanh n i 2: lề ố 2 = 0,4 m
Kh i l ng thanh n i 1: mố ượ ố 1 = 1 Kg
Kh i l ng thanh n i 2: mố ượ ố 2 = 1 Kg
Momen quán tính kh p 1 quay quanh tâm kh i: Jớ ố 1 = 0,5 Kgm2
Momen quán tính kh p 2 quay quanh tâm kh i: Jớ ố 2 = 0,5 Kgm2
Kho ng cách t kh p 1 đ n tâm thanh n i 1: lả ừ ớ ế ố g1 = 0,25 m
Kho ng cách t kh p 2 đ n tâm thanh n i 2: lả ừ ớ ế ố g2 = 0,2 m
Góc ban đ u c a các thanh n i: θầ ủ ố 1 = 0 rad ; θ2 = Л/6 rad
Góc đ t c a các thanh n i: θặ ủ ố 1 = Л/3 rad ; θ2 = Л/2 rad
1. Xây d ng mô hình robotự
Gi thi t kh p 1 sinh ra momen Mả ế ớ 1 tác d ng gi a b và thanh n i 1;ụ ữ ệ ố
kh p 2 sinh ra momen Mớ2 tác d ng gi a thanh n i 1 và 2; tr ng l c có h ngụ ữ ố ọ ự ướ
theo tr c yụ
Ký hi u đ ng năng và th năng c a thanh n i i là Kệ ộ ế ủ ố i và Pi (i=1,2)
Ta có:
Đ ng năng thanh n i 1:ộ ố
Th năng thanh n i 1:ế ố
T a đ tâm kh i thanh n i 2:ọ ộ ố ố
T c đ tâm kh i thanh n i 2:ố ộ ố ố
→Bình ph ng t c đ dài tâm thanh n i 2:ươ ố ộ ố
Đ ng năng thanh n i 2:ộ ố
Th năng thanh n i 2:ế ố
Hàm lagrange c a robot:ủ
Mômen c a kh p 1:ủ ớ
Mômen c a kh p 2:ủ ớ
Đ t ặ,
Ta có mô hình toán h c robot:ọ
Trong đó:
: ma tr n quán tínhậ
V i: ớ
: thành ph n momen nh t và h ng tâmầ ớ ướ
: thành ph n momen tr ng l cầ ọ ự
V i: ớ
Th c hi n mô ph ng trên matlab:ự ệ ỏ
Mô hình trên matlab:
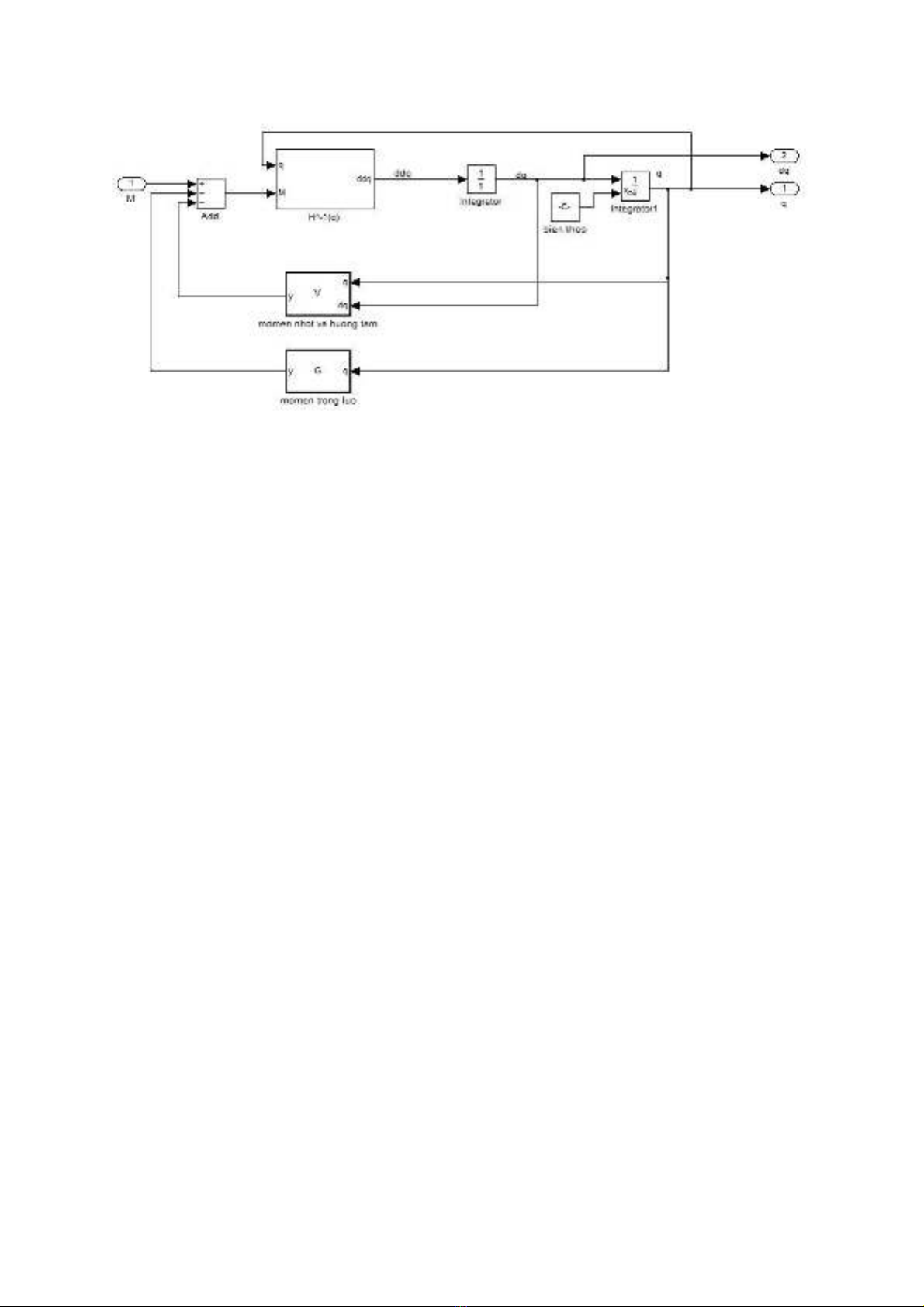
Trong đó:
- Hàm tính G:
function y = G(q)
% thong so ro bot
m1 = 1; m2 = 1;
l1 = 0.5; l2 = 0.4;
g = 9.8;
J1 = 0.5; J2 = 0.5;
lg1= l1/2; lg2 = l2/2;
% ma tran G
g1 = m1*g*lg1*cos(q(1))+m2*g*[l1*cos(q(1))+lg2*cos(q(1)+q(2))];
g2 = m2*g*lg2*cos(q(1)+q(2));
y = [g1;g2];
- Hàm tính V:
function y = V(q,dq)
% thong so robot
m1 = 1; m2 = 1;
l1 = 0.5; l2 = 0.4;
g = 9.8;
J1 = 0.5; J2 = 0.5;
lg1= l1/2; lg2 = l2/2;
% ma tran V
V1 = -m2*l1*lg2*sin(q(2))*[dq(2)^2+2*dq(1)*dq(2)];
V2 = m2*l1*lg2*sin(q(2))*dq(1)^2;
y = [V1;V2];
- Kh i ố
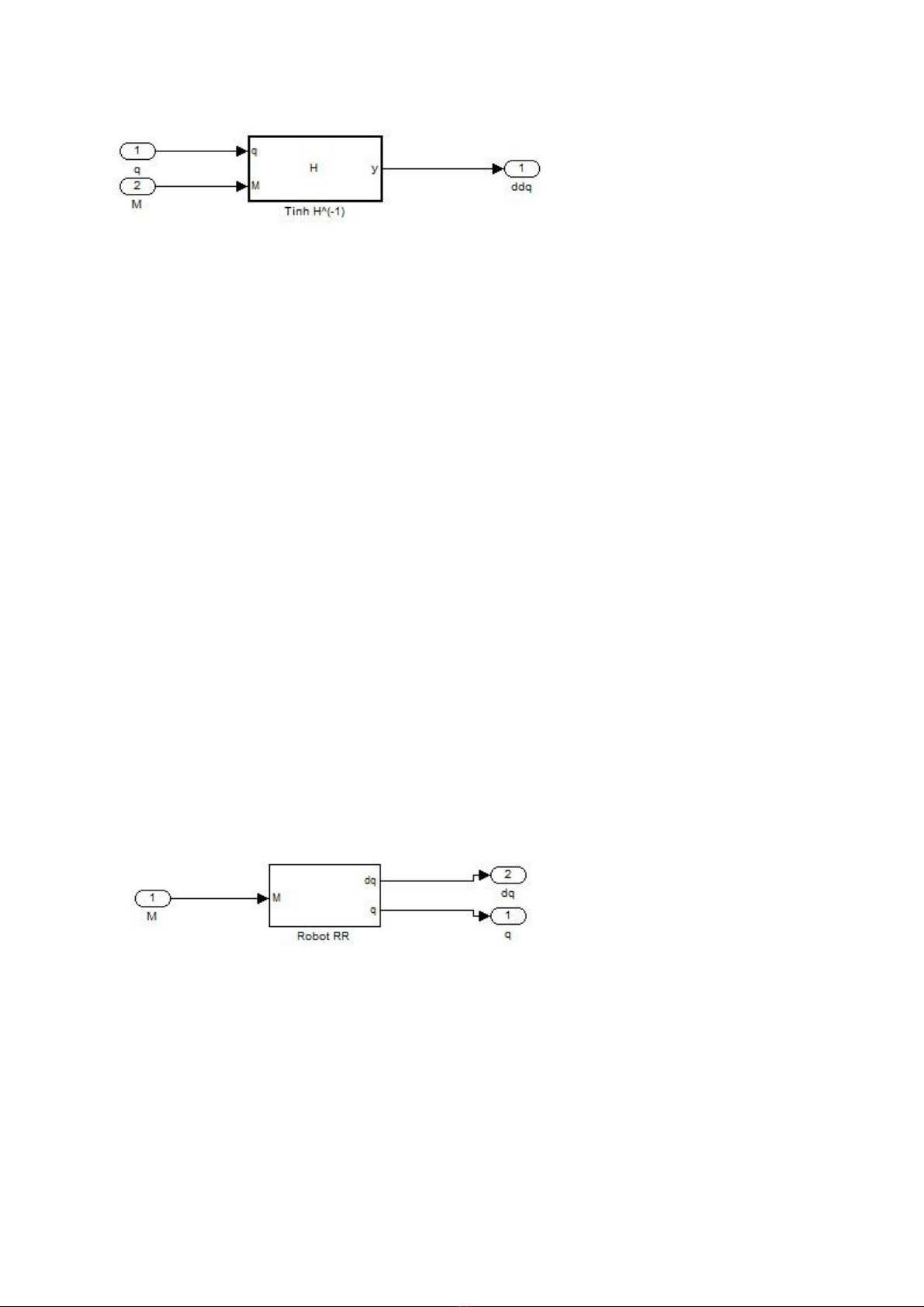
Hàm tính
function y = H(q,M)
% thong so robot
m1 = 1; m2 = 1;
l1 = 0.5; l2 = 0.4;
g = 9.8;
J1 = 0.5; J2 = 0.5;
lg1 = l1/2; lg2 = l2/2;
% bien khop
theta1=q(1);
theta2=q(2);
% ma tran H(q)
H11=m1*lg1^2+J1+m2*(l1^2+lg2^2+2*l1*lg2*cos(theta2))+J2;
H12=m2*(lg2^2+l1*lg2*cos(theta2))+J2;
H21=H12;
H22=m2*lg2^2+J2;
H = [H11 H12;H21 H22];
% ma tran nghich dao H^(-1)(q)
Hinv = inv(H);
% Gia toc khop
y = Hinv * M;
T o kh i robot (Create Subsystem)ạ ố