BÀI T P L NẬ Ớ
LÝ THUY T M CHẾ Ạ
B GIÁO D C VÀ ĐÀO T OỘ Ụ Ạ
TR NG Đ I H C GIAO THÔNG V N T IƯỜ Ạ Ọ Ậ Ả
___ o O o ___
Chuyên ngành : K thu t Thông Tin & Truy n Thôngỹ ậ ề
Khóa : 49
Giáo viên h ng d nướ ẫ : Ths. Nguy n Công Th ngễ ắ
Sinh viên : Nhom 3
Nguyên Đ c Chinh ư
Hoang Văn D ư
Đô Văn Hiêu
Vu Quôc Huy
Trân Trong Ngoc
Nguyên Thê Quân
Ha Thanh S n ơ
Trân Hoang Thinh
Nguyên Kiêu Trang
Tô Manh Tuân
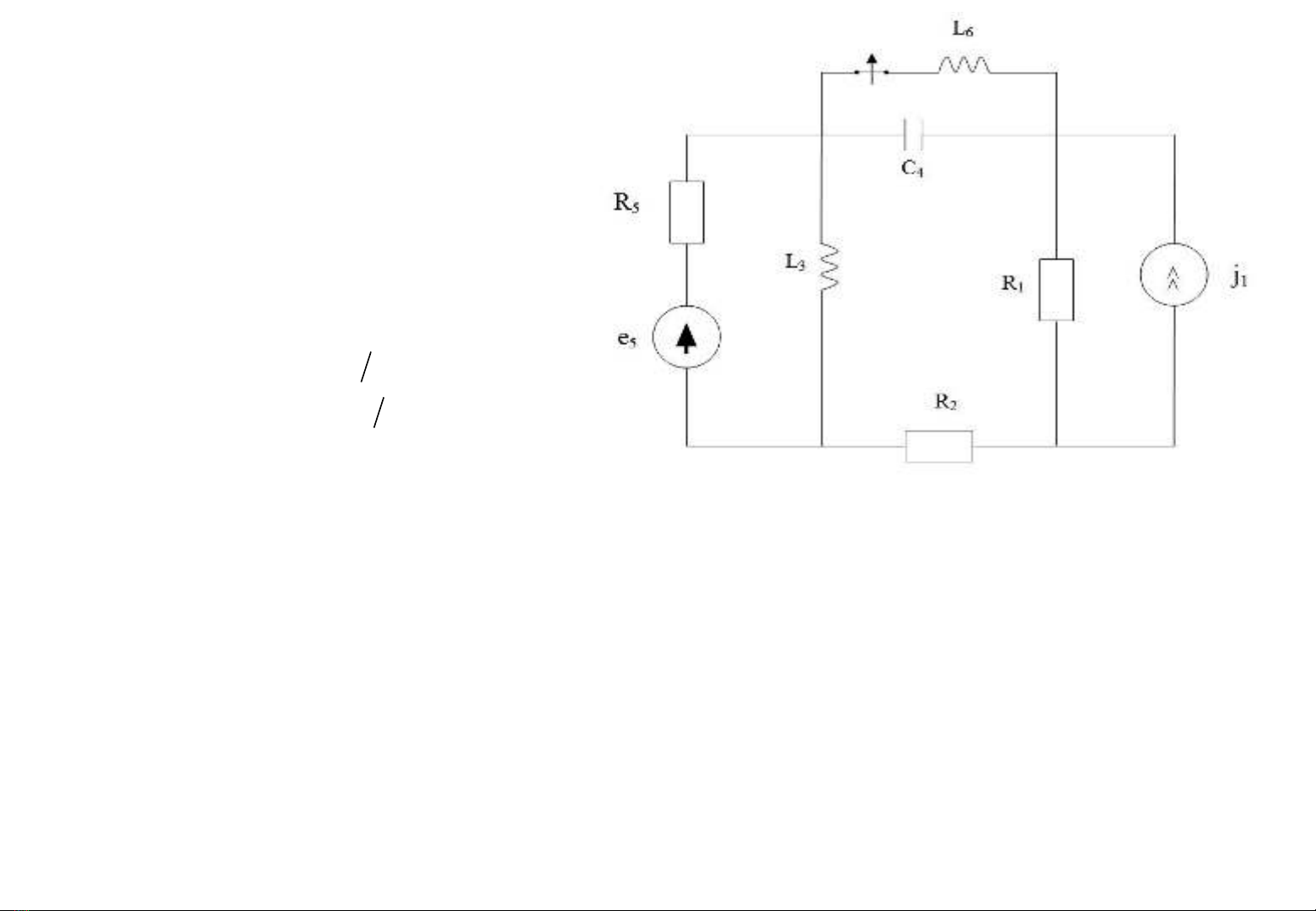
•Cho m ch đi n có các s li u sau:ạ ệ ố ệ
N I DUNGỘ
Hzf
Attj
Vtte
FC
LHL
R
RR
50
)6cos(41.1)(
)3sin(150)(
;150
;15.0;18.0
;18
;15;20
4
63
5
21
=
+=
+=
=
Ω==
Ω=
Ω=Ω=
πω
πω
µ
I. Tìm m i dòng đi n xác l p khi khóa K ch a tác đ ng b ngọ ệ ậ ư ộ ằ :
a. Ph ng pháp dòng đi n nhánh v i h c mươ ệ ớ ỗ ả
b. Ph ng pháp dòng đi n vòng v i h c mươ ệ ớ ỗ ả
c. Ph ng pháp đi n th nút khi h c m v iươ ệ ế ỗ ả ớ
II. Tìm dòng đi n xác l p trên m t nhánh b t kỳ theo ph ng pháp máy phát đi n t ng đ ngệ ậ ộ ấ ươ ệ ươ ươ (Đ nh lý ị
Thevenin ho c đ nh lý Norton) v i h c mặ ị ớ ỗ ả
III. Tìm dòng đi n quá đ trên cu n c m và đi n áp quá đ trên t đi n b ng ph ng pháp toán t sau ệ ộ ộ ả ệ ộ ụ ệ ằ ươ ử
khi khóa K tác đ ng.ộ
a. Xác đ nh các đi u ki n ban đ uị ề ệ ầ
b. L p h ph ng trình tr ng tháiậ ệ ươ ạ
c. Tìm nghi m – đáp ng nh I1(p); Uc(p)ệ ứ ả
d. Xác đ nh nghi m th i gian i1(t); Uc(t)ị ệ ờ
)(0 HM
=
HM 1.0
=
HM 1.0
=
)(0 HM
=
*
*
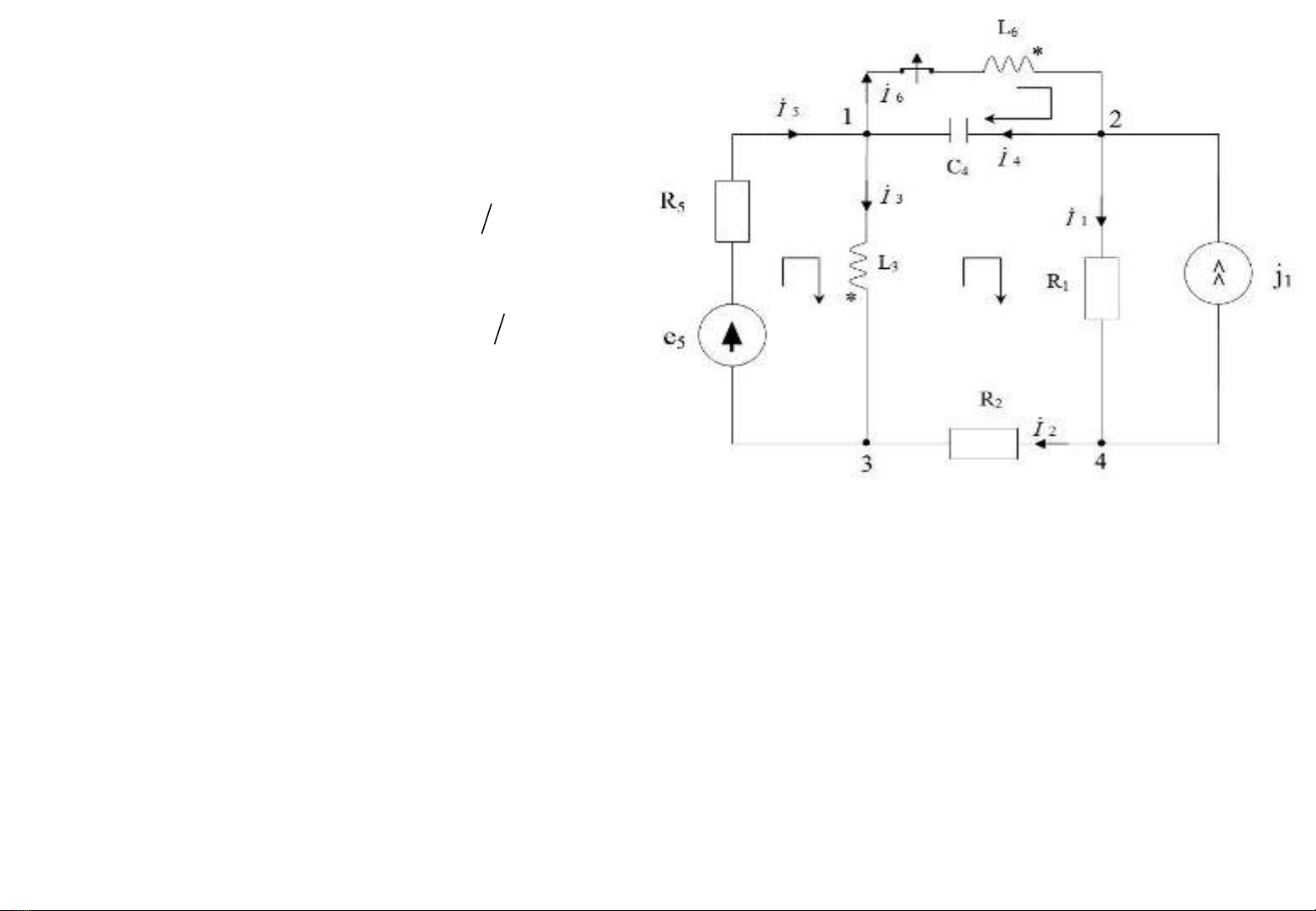
•Ta có:
- Ch n chi u dòng đi n và vòng nh hình v . ọ ề ệ ư ẽ
- Ta co h ph ng trình vi t theo ph ng ệ ươ ế ươ
pháp dòng đi n nhánh:ệ
3 3
6 6
4
5
1
2 100
56.55
47.12
21.22
( ) 150sin( 3)
53.03 91.86
( ) 1.41cos( 6)
0.50 0.86
L
L
C
f
Z i L i
Z i L i
Z i
e t t
E i
j t t A
J i
ω π π
ϖ
ϖ
ω π
ω π
= =
= =
= =
= −
= +
= +�
= +
= − +�
g
g
3 4 5 6
1 4 6 1
2 3 5
5 3 6 5
5 3
1 2 3 4 6
1 2 3 4
3 4 6
4 6
0
0
0
0
L M
L C M
M C L
I I I I
I I I J
I I I
I R I Z I Z E
I R I R I Z I Z I Z
I Z I Z I Z
− + + − =
− − + = −
+ − =
+ + =
+ − − − =
+ + =
g g g g
g g g g
g g g
g g g g
g g g g g
g g g
I. Tìm dòng đi n xác l p khi khóa K ch a tác ệ ậ ư
đ ng.ộ
a. Ph ng pháp dòng đi n nhánh:ươ ệ
Gi i h ph ng trình trên b ng Matlab ta đ c k t qu :ả ệ ươ ằ ượ ế ả
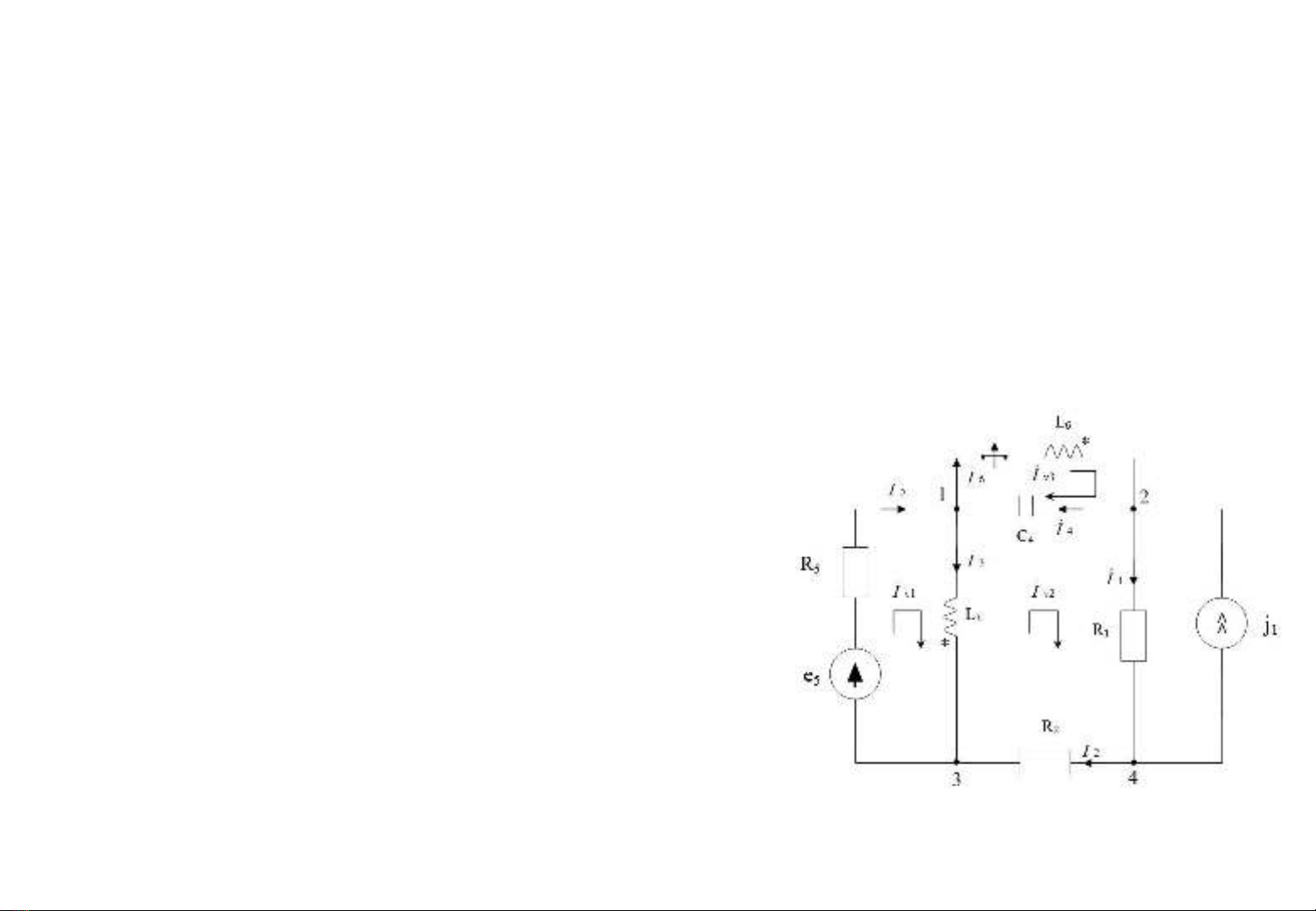
b. Ph ng phap dong điên ươ
vong
Ch n bi n là các dòng đi n vòng nh hình v . ọ ế ệ ư ẽ
H ph ng trình vi t theo ph ng pháp dòng đi n vòng:ệ ươ ế ươ ệ
1
1
22
33
4
4
5
5
6
1.31 2.46 ( ) 3.94sin(314 118 )
0.81 1.60 ( ) 2.53sin(314 117 )
( ) 2.74sin(314 12 )
1.89 0.40
( ) 4.94sin(314 103 )
0.82 3.40
(
1.08 2.00
1.63 1.80
o
o
o
o
I i i t t
I i i t t
i t t
I i
i t t
I i
i
I i
I i
= − +
= +
= − +
= +
= +
= +
= −
= − −
= +
= − −
g
g
g
g
g
g6
) 3.22sin(314 62 )
( ) 3.43sin(314 132 )
o
o
t t
i t t
= +
= −
v1 v2 v3 5
5 3 3
v1 v2 v3 1
3 1 2 3 4 1
v1 v2 v3
4 4 6
I ( ) I I E
I I ( ) I ( ) J
I I ( ) I ( ) 0
L L M
L L C M C
M M C C L
R Z Z Z
Z R R Z Z Z Z R
Z Z Z Z Z
+ − + =
− + + + + + − − = −
+ − − + + =
g g g g
g g g g
g g g
Gi i h ph ng trình trên b ng Matlab ta đ c k t qu :ả ệ ươ ằ ượ ế ả
v1
v2
v3
1.08 2.00
0.81 1.60
1.63 1.80
I i
I i
I i
= +
= − +
= − −
g
g
g
Trong đo:
1 2 1
1
1
2 2 2
3 1 2 3
4 3 2 4
5 1 5
6 3 6
1.31 2.46 ( ) 3.94sin(314 118
0.81 1.60
1.89 0.40
0.82 3.40
1.08 2.00
1.63 1.80
v
v
v v
v v
v
v
I I J I i i t t
I I I i
I I I I i
I I I I i
I I I i
I I I i
� �
= + = − +
� � = +
� �
= = − +
� �
� �
= − = +
� �
� �
� �
� �
= − = − −
� �
� �
= = +
� �
� �
= = − −
� �
g g g g
g g g
g g g g
g g g g
g g g
g g g
2
3
4
5
6
)
( ) 2.53sin(314 117 )
( ) 2.74sin(314 12 )
( ) 4.94sin(314 103 )
( ) 3.22sin(314 62 )
( ) 3.43sin(314 132 )
o
o
o
o
o
o
i t t
i t t
i t t
i t t
i t t
= +
= +
= −
= +
= −