Đ I H C ĐÀ N NGẠ Ọ Ẵ
TR NG Đ I H C BÁCH KHOAƯỜ Ạ Ọ
KHOA ĐI NỆ

BÀI T P DÀIẬ
MÔN :LÍ THUY T M CH 2Ế Ạ
Sinh viên th c hi nự ệ : PHAN NG C HI NỌ Ể L p :04ĐTĐớ
Giáo viên h ng d nướ ẫ : TS Hoàng Dũng
S đ : 11 . C t s li u :4Cơ ồ ộ ố ệ
Đà N ng 2006ẵ
L1
1mH
j
K
R
C
L
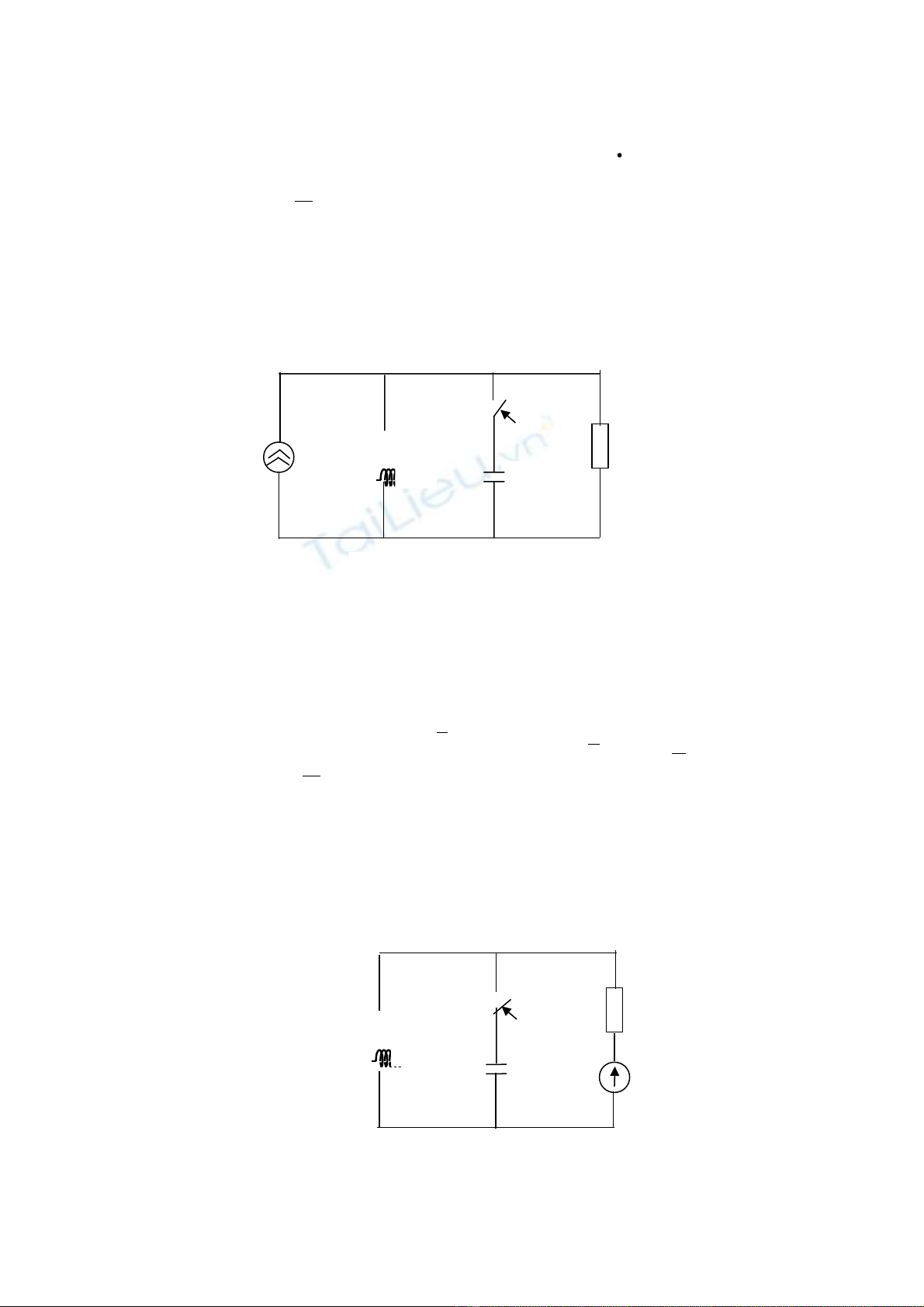
S đ m ch đi n .ơ ồ ạ ệ
L1
1mH
Đ bài :Tính quá trình quá đ trong m ch đi n tuy n tính h s h ng. ề ộ ạ ệ ế ệ ố ằ
Cho m ch đi n nh hình v -ngu n dòng có ạ ệ ư ẽ ồ
srad /1000=
ω
và biên đ Jộm=10.Quá
trình đóng m ch x y ra khi giá tr t c th i c a ngu n dòng đi n J=kJạ ả ị ứ ờ ủ ồ ệ m,v i k=-1/2 vàớ
có xu h ng tăng ướ
0>
dt
dj
.
1.B ng ph ng pháp tích phân kinh đi n và ph ng pháp toán t tính dòng quá đằ ươ ể ươ ử ộ
c a m t trong các nhánh song song không có đi n c m hay ngu n cung c p .ủ ộ ệ ả ồ ấ
2.V đ th dòng đi n i(t) tìm đ c .ẽ ồ ị ệ ượ
Trong đó :R=10
Ω
, L=10-2H, C=0,5.10-4F
Bài làm:
I. Tính các s li u ban đ uố ệ ầ :
Khi K đóng m ch ,m ch ch đ xác l p ngu n đi u hòa ạ ạ ở ế ọ ậ ồ ề
srad /1000
=
ω
.
)sin()(
ϕω
+= tJtj m
Lúc t=0: theo đ ề
6
0)cos(
2
1
)sin(
0)cos(
2
1
)sin()0(
π
ϕ
ϕ
ϕ
ϕω
ϕ
−=⇒
>
−=
⇒
>=
−==
m
mm
J
dt
dj
JJj
V y ta có :j=10sin(1000t-30ậ0) (A).
Đ đ n gi n vi c tính toán sau này ,ta g i s ngu n dòng khép m ch qua đi n trể ơ ả ệ ả ử ồ ạ ệ ở
R ,ta quy ngu n dòng v ngu n su t đi n đ ng t ng đ ngồ ề ồ ấ ệ ộ ươ ươ
e(t)=R.j=100sin(1000t-300) V
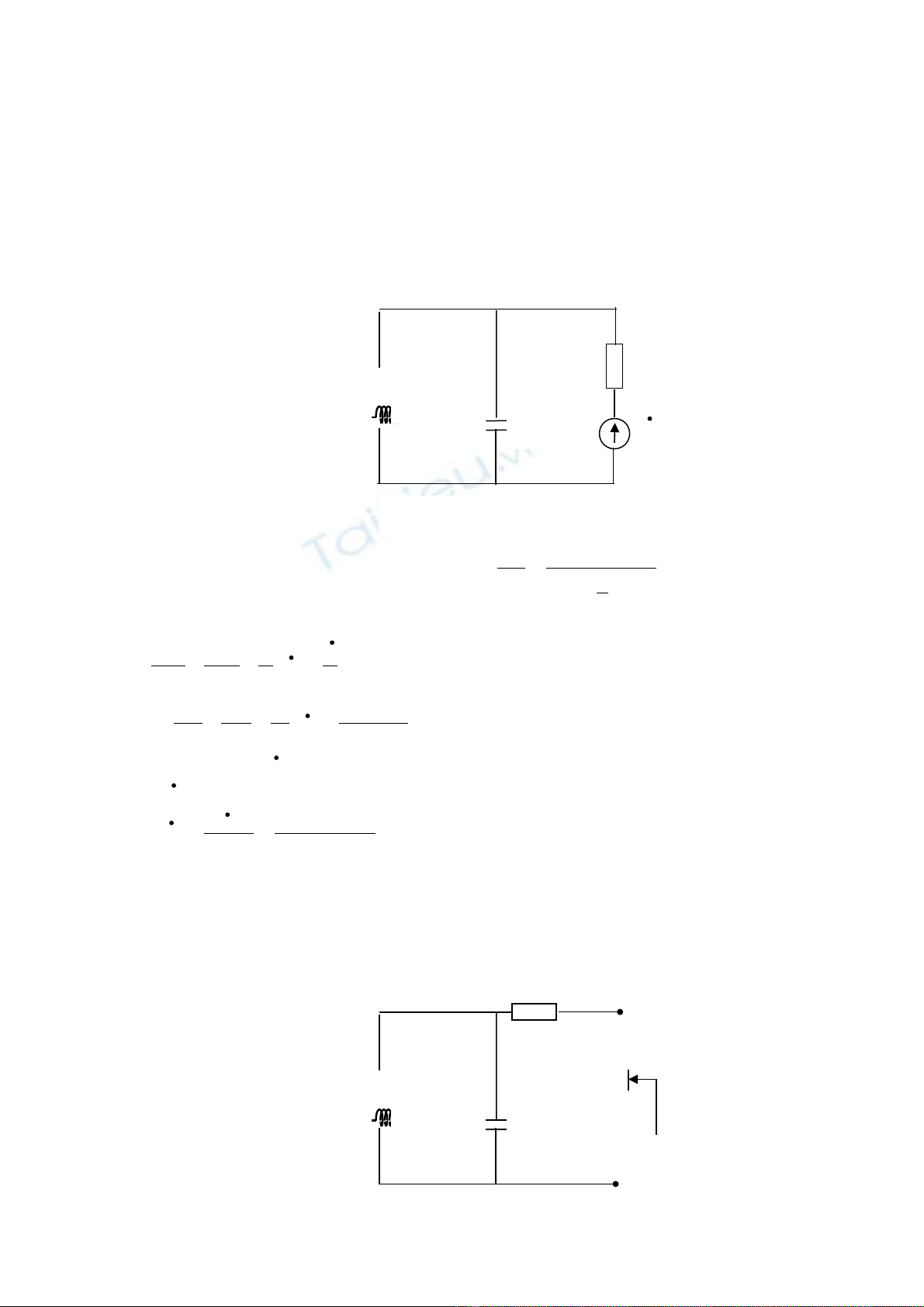
Ta có s đ thay th sauơ ồ ế :
K
e(t)
R
L
C
S đ m ch đi n t ng đ ngơ ồ ạ ệ ươ ươ
Zv(p)
L1
1mH
L1
1mH
1/pC
II. Tính dòng đi n quá đệ ộ :
Ta tính dòng đi n quá đ cho nhánh C.ệ ộ
1.Ph ng pháp tích phân kinh đi nươ ể :
Ta có :
iCqd= iCxl + iCtd
a.Tính dòng đi n ch đ xác l p sau khi đóng khóa Kệ ở ế ộ ậ : iCxl
Ph c hóa s đò m ch ta đ cứ ơ ạ ượ :
Trong đó :
Ω=== −1010*1000 2
LX L
ω
Dùng ph ng pháp đi n th đ nh ta cóươ ệ ế ỉ :
R
E
RjXjX a
CL
=
+−
ϕ
111
10
30100
10
1
20
1
10
10
∠
=
+−⇒ a
jj
ϕ
( )
jj a566,81,005,0 −=+−⇒
ϕ
)(36,528,89 Vj
a−=⇒
ϕ
)(8647,4464,4268,0
20
36,528,89 0Aj
j
j
jX
I
C
a
C∠=+=
−
−
=
−
=⇒
ϕ
V yậ :iCxl=4,47sin(1000t+860) A
b.Tính dòng đi n t doệ ự :iCtd
- Dòng t do có d ng iự ạ Ctd=Aept
- Xác đ nh s mũ đ c tr ng p: Ng n m ch ngu n S.đ.đ và h m ch t i đó ,toánị ố ặ ư ắ ạ ồ ở ạ ạ
t hóa ta đ c s đ sau:ử ượ ơ ồ
E
R
jXL
-jXc
S đ m ch đi n t ng đ ngơ ồ ạ ệ ươ ươ
R
pL
11
1
1
)( 2
2
2+
++
=
+
+=
+
+= LCp
RpLRLCp
LCp
pL
R
pC
pL
pC
pL
RpZv
Zv(p)=0
0
2=++⇒ RpLRLCp
0101010.
2
1
.10.10 2242 =++⇔ −−− pp
jppp 100010000101010.5 226 ±−=⇔=++⇔ −−
Nh v y d ng c a iư ậ ạ ủ Ctd s là : ẽ
))(1000cos(2 1000 AtAei t
Ctd
ψ
+= −
(1)
Theo (1) thì ta c n ph i xác đ nh 2 thành ph n c a iầ ả ị ầ ủ Ctd là A và
ψ
do đó ta c n ph iầ ả
tính hai s ki n , đây ta tính 2 s ki n ph thu c là iơ ệ ở ơ ệ ụ ộ C(0) và i’C(0).
b1.Tính các s ki n đ c l p iơ ệ ộ ậ L(0) và uC(0);
b11. Tính iL(0):
Xét m ch đi n tr c đóng K. Vì m ch ch đ xác l p nên ta dùng s ph cạ ệ ướ ạ ở ế ộ ậ ố ứ
đ tính iểL(t).Ta có :
)(1051,783,683,1
1010
30100 0
0
Aj
jjXR
E
I
L
L∠=+−=
+
−∠−
=
+
−
=
))(1051000sin(1,7)( 0AttiL+=⇒
(*)
Thay t=0 vào (*) ta đ c iượ L(-0)= 6,86 A
Vì bài toán ch nh nên ta có iỉL(-0) = iL(0) = 6,86 A
b12. Tính uC(0) :
Vì tr c đóng K uướ C ch a n p đi n và bài toán ch nh nên uư ạ ệ ỉ C(-0)=uC(0)=0
b2.Tính các s ki n iơ ệ C(0) và i’C(0) :
H ph ng trình theo t mô t m ch sau khi đóng Kệ ươ ả ạ
)3(
)2(
)1(
)()()(
0)()(
0)()()(
'
tetutRi
tutLi
tititi
CR
CL
RCL
−=−
=−
=−−
+−
=
=
−=
⇔
R
tute
ti
tutLi
tititi
c
R
CL
CLC
)()(
)(
)()(
)()()(
'
Thay t=0 vào h ph ng trình trên ta cóệ ươ :
==
=
=−=
⇔
+−
=
=
−=
⇔
Ai
i
Ai
R
ue
i
uLi
iii
R
L
C
c
R
CL
RLC
5
10
50
)0(
0)0(
8,158,6)0(
)0()0(
)0(
)0()0(
)0()0()0(
''
Đ o hàm hai v ph ng trình (1) và (3) ta đ cạ ế ươ ượ :
−=−
=−
=−−
)()(
1
)(
0)()(
0)()()(
''
'
'''
teti
C
tRi
tutLi
tititi
CR
CL
RCL
(**)
Thay t=0 vào (**) ta đ cượ :
L1
1mH
Li(0)
−=−
=−
=−−
)0()0(
1
)0(
0)0()0(
0)0()0()0(
''
'
'''
ei
C
Ri
uLi
iii
CR
CL
RCL
+
−
=
=
−=
⇔
)0(
1)0(
)0(
0)0(
)0()0(
'
'
'
''
CR
L
RC
i
RCR
e
i
i
ii
−=+
−
=
=
=−=
⇔
−)/(10.506,08,1
10.5
1
10
10.66,8
)0(
0)0(
)/(10.506,0)0()0(
4
4
4
'
'
4''
sAi
i
sAii
R
L
RC
b3.Xác đ nh A và ị
ψ
.
Dòng đi n quá đ có d ng:ệ ộ ạ
))(1000cos(2)861000sin(47,4 10000 AtAeti t
Cqd
ψ
+++= −
)/)(1000sin(2000)1000cos(2000)861000cos(4470 100010000' sAtAetAeti tt
Cqd
ψψ
+−+−+= −−
Ta l i có :ạ
30
0
0'
0
10.06,5)sin(cos200086cos4470
8,1cos286sin47,4
)sin(cos200086cos4470)0(
cos286sin47,4)0(
=+−
=+
⇔
+−=
+=
ψψ
ψ
ψψ
ψ
A
A
Ai
Ai
Cqd
Cqd
=
−=
⇔
=
−
=
⇔
=+
−
=
⇔
−=+
−=
⇔0
38
69,1
785,0
cos
33,1
785,1
cos
sin
1
cos
33,1
37,2)sin(cos
33,1cos
ψ
ψψ
ψ
ψψ
ψψ
ψ
A
tg
A
A
A
A
Do đó :iCtd= -3,38e-1000tcos(1000t+380) (A).
V y dòng đi n quá đ qua nhánh C là :ậ ệ ộ
iCqd(t) = 4,47sin(1000t+860) – 3,38e-1000tcos(1000t+380) (A)
2.Ph ng pháp toán t Lapaceươ ử :
Toán t hóa s đ m ch đi n sau đóng K ta đ cử ơ ồ ạ ệ ượ :
V i ớ
6262 10
8665,0
100
10
)30cos(1000)30sin(
100)( +
+−
=
+
−+−
=p
p
p
p
pE
Và iL(0) = 6,8 A
Ta gi i m ch b ng ph ng pháp đi n th đ nhả ạ ằ ươ ệ ế ỉ :
a
E(p)
R
pL 1/pC
S đ m ch đi n t ng đ ngơ ồ ạ ệ ươ ươ