Biênsoạn:BộmônCUD‐VCK 1
VCK‐BộmônCơứngdụng
BàitậpRobotics
1. Xácđịnhsốbậctựdo
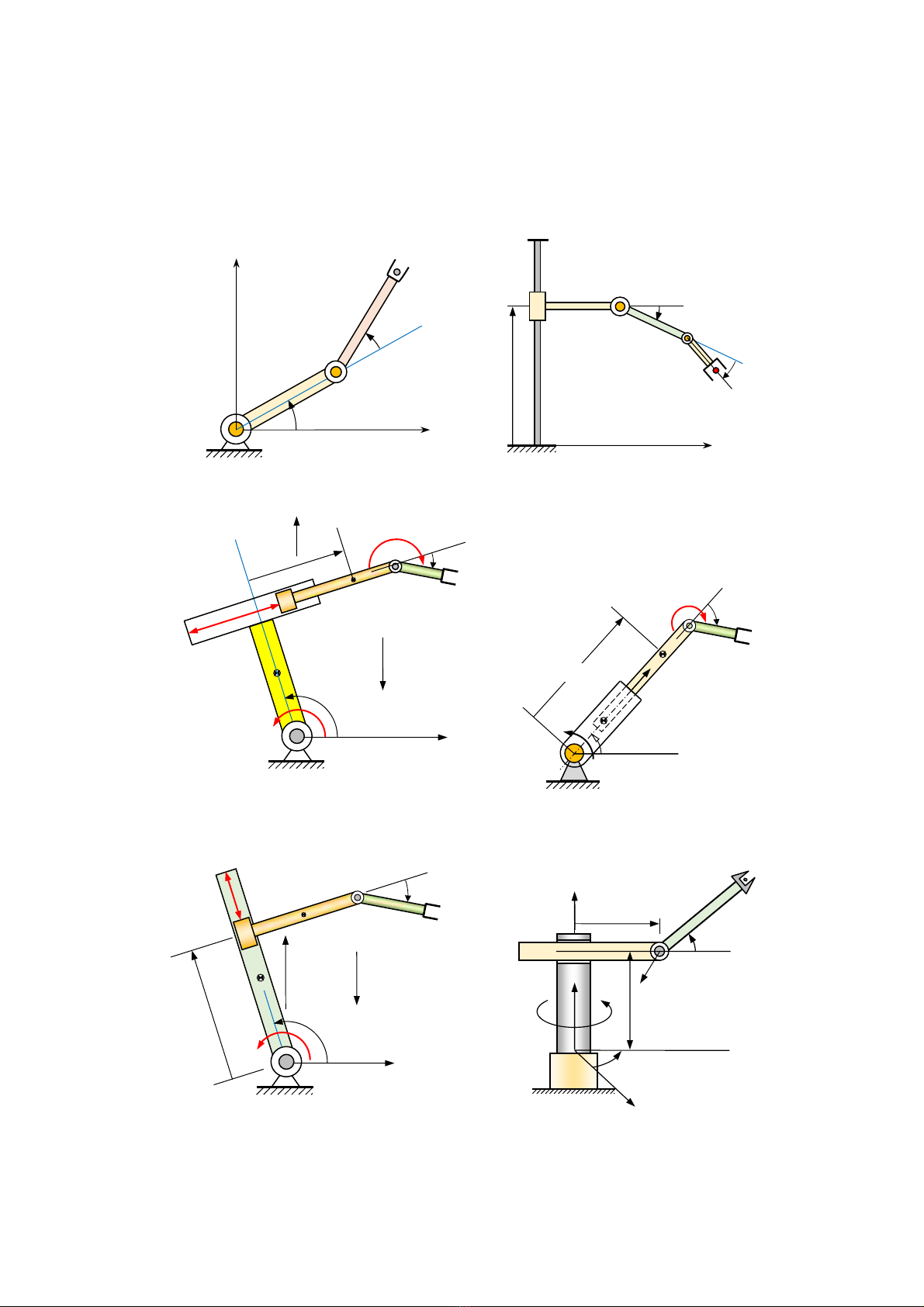
1‐1Xácđịnhsốbậctựdocủacáctaymáyrobotchuỗichotrêncáchìnhsau:
H. bài Tay máy phẳng RRR
O
C
1
C2
u1
u2
u
q3
u3
O
q1
q2
g
x0
E
C1
C2
A
B
y0
u1
u2
H. bài Tay máy phẳng RTR
q3
O
q1
q2
g
x0
E
A
B
C2
C1
y0
u1
u2
H. bài Tay máy phẳng RTR
q3
u3
x
q1
q2
q3
E
y
l3
l2
l1
H. bài Tay máy phẳng TRR
H. bài Tay máy không gian RTR
z2
q3
z0
l3
E
z1
q1
q2
x0
x1
d1
O0
A
1
O
q1
y
x
E
q2
H. bài Tay máy phẳng RR
l1
l2
Biênsoạn:BộmônCUD‐VCK 2
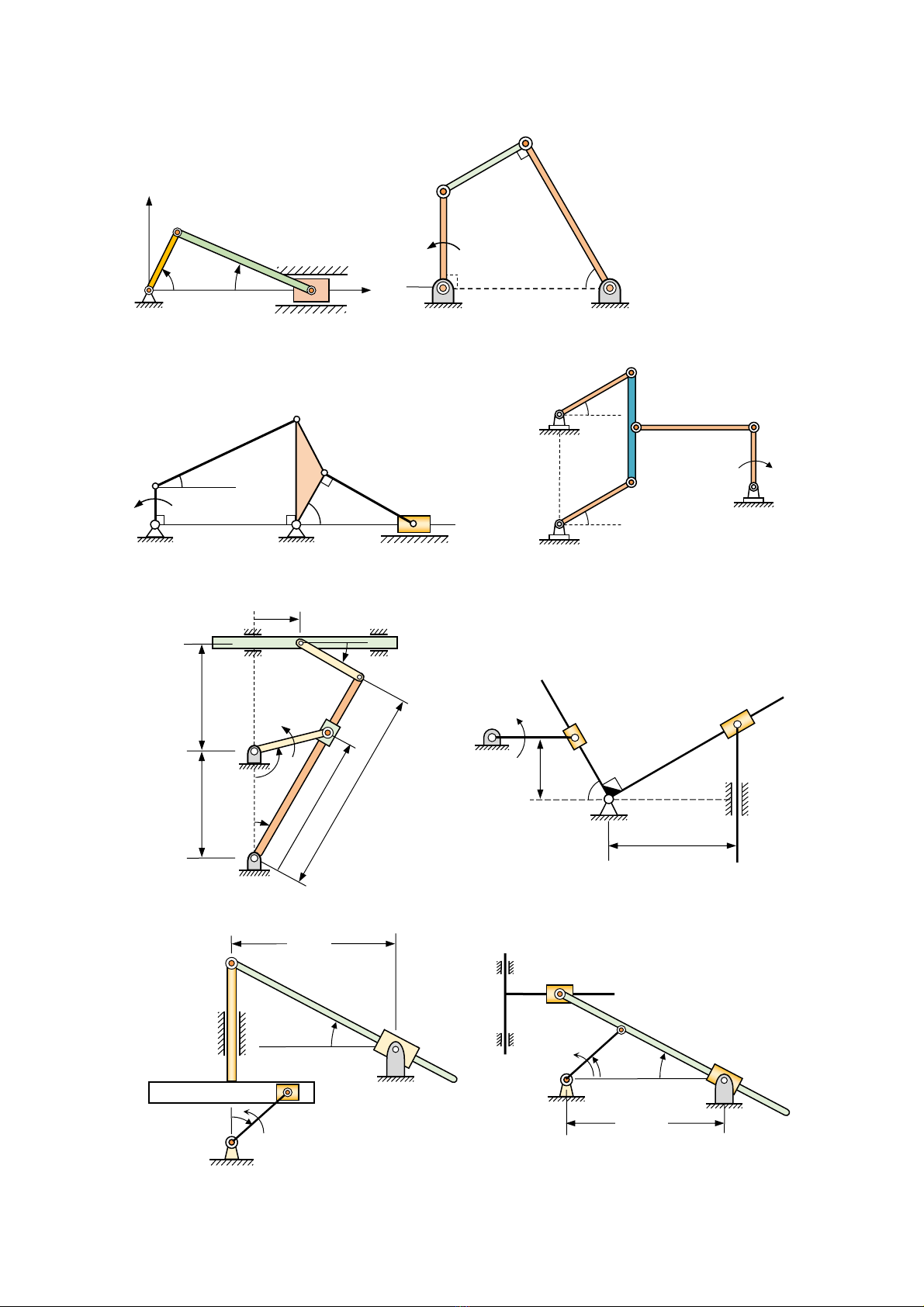
1‐2Xácđịnhsốbậctựdocủacáccơcấuvàtaymáyrobotsongsongchotrêncáchìnhsau:


 
H. bài
60
30
O
A
B
C
D
E
0
w
H. bài
C
D
B
A
O
,wa
K
0.25 m
H. bài
C
D
B
A
O ,wa
K
0.2 m
H. bài
F
C
E
D
B
A
,wa
O
30 cm
15 cm
O
B
A
0
C
E D
x
H. bài
h
h
u
L
l
C
B
A
O
0
w
H. bài
30
D
E
F
30
0
w
O
A
B
C
H bμi
A
O
B
x
y
H bài

r L
Biênsoạn:BộmônCUD‐VCK 3



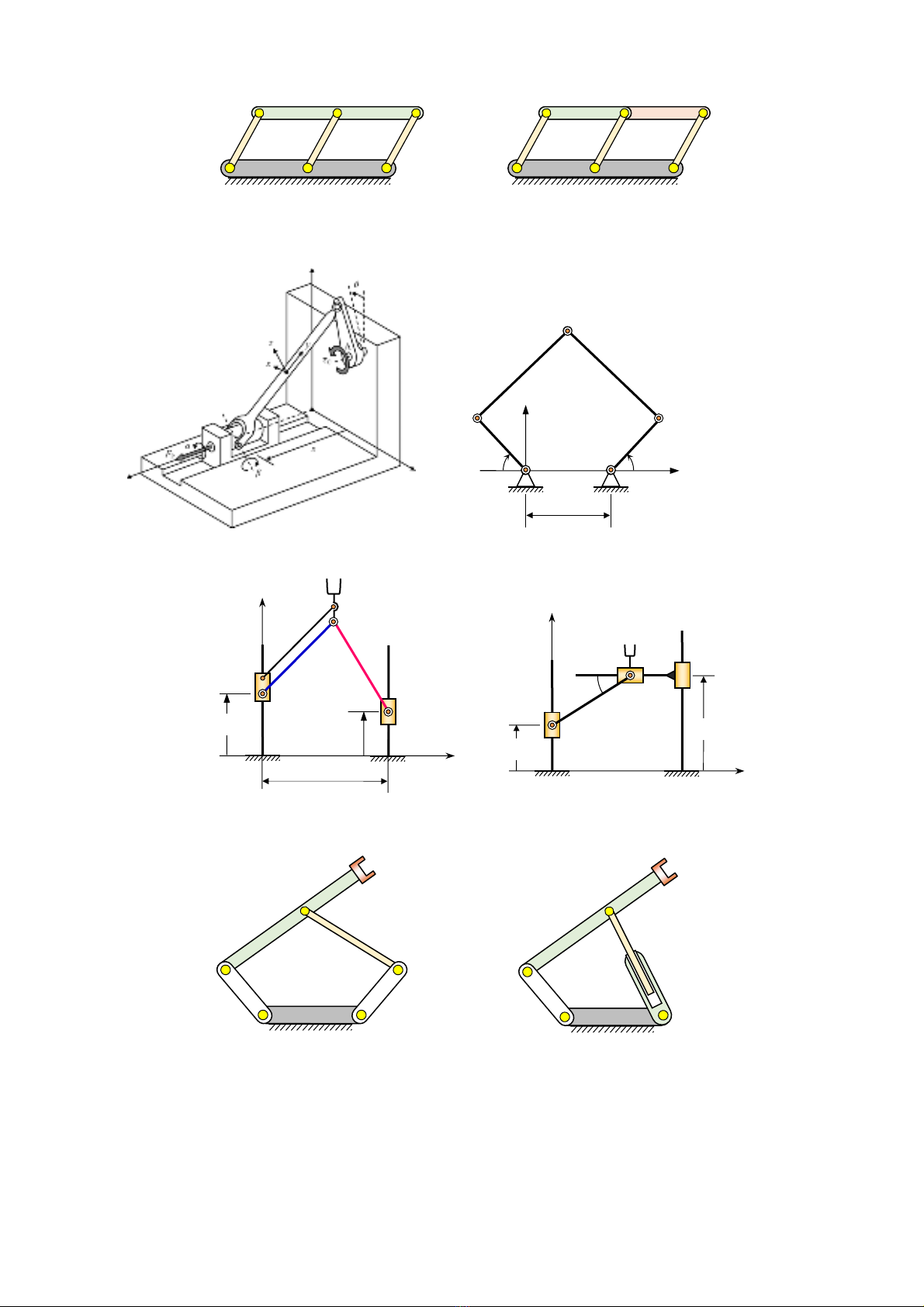
H. bài Tay máy song song, 4R1P
H. bài Tay máy song song, 5R
Cơ cấu 5 khâu hình bình hành Cơ cấu 6 khâu hình bình hành
O
A
B
C
D
y
x
l1
l2l2
l1
l0
2
1
Robot song song phẳng
Cơ cấu tay quay – con trượt không gian
A
B
C
Ox
y
l
s1(t)
s2(t)
30
Robot song song phẳng
A
B
C
O
x
y
l1
l2
l0
s1(t) s2(t)
l1
Robot song song phẳng
Biênsoạn:BộmônCUD‐VCK 4


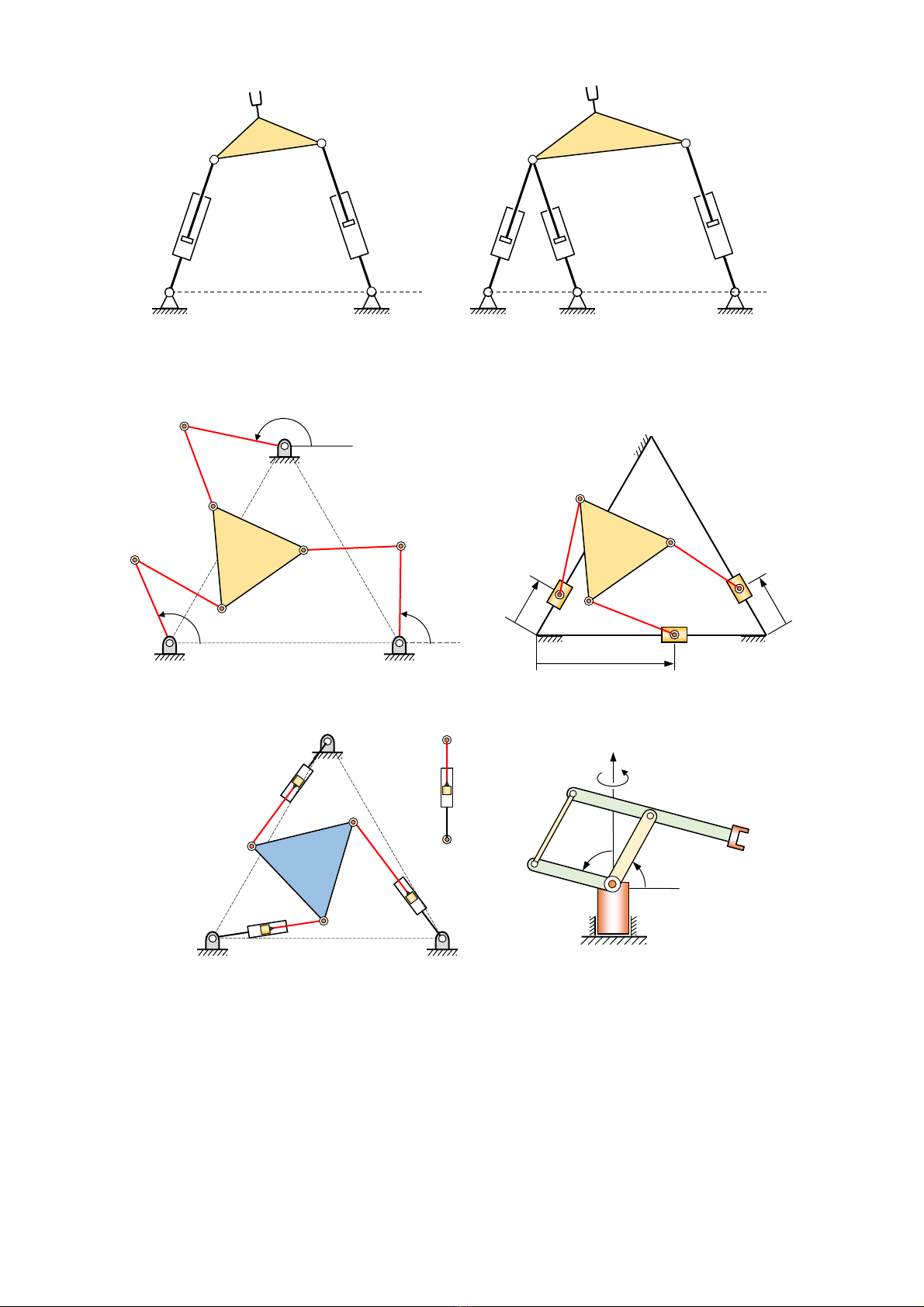
Tay máy không gian sử dụng cơ
cấu hình bình hành
q1
q3
q2
q3
q1
q2
7
Robot song song phẳng 3RTR
q1
q2
q3
Robot song song phẳng 3TRR
q3
q1 q2
1 2
3
4
7
5
6
Robot song song phẳng 3RRR
Hệ phẳng 8 khâu
Hệ phẳng 6 khâu
A B
C
O
A
B
C
OD
l0
ll
l01 l02
Biênsoạn:BộmônCUD‐VCK 5

 

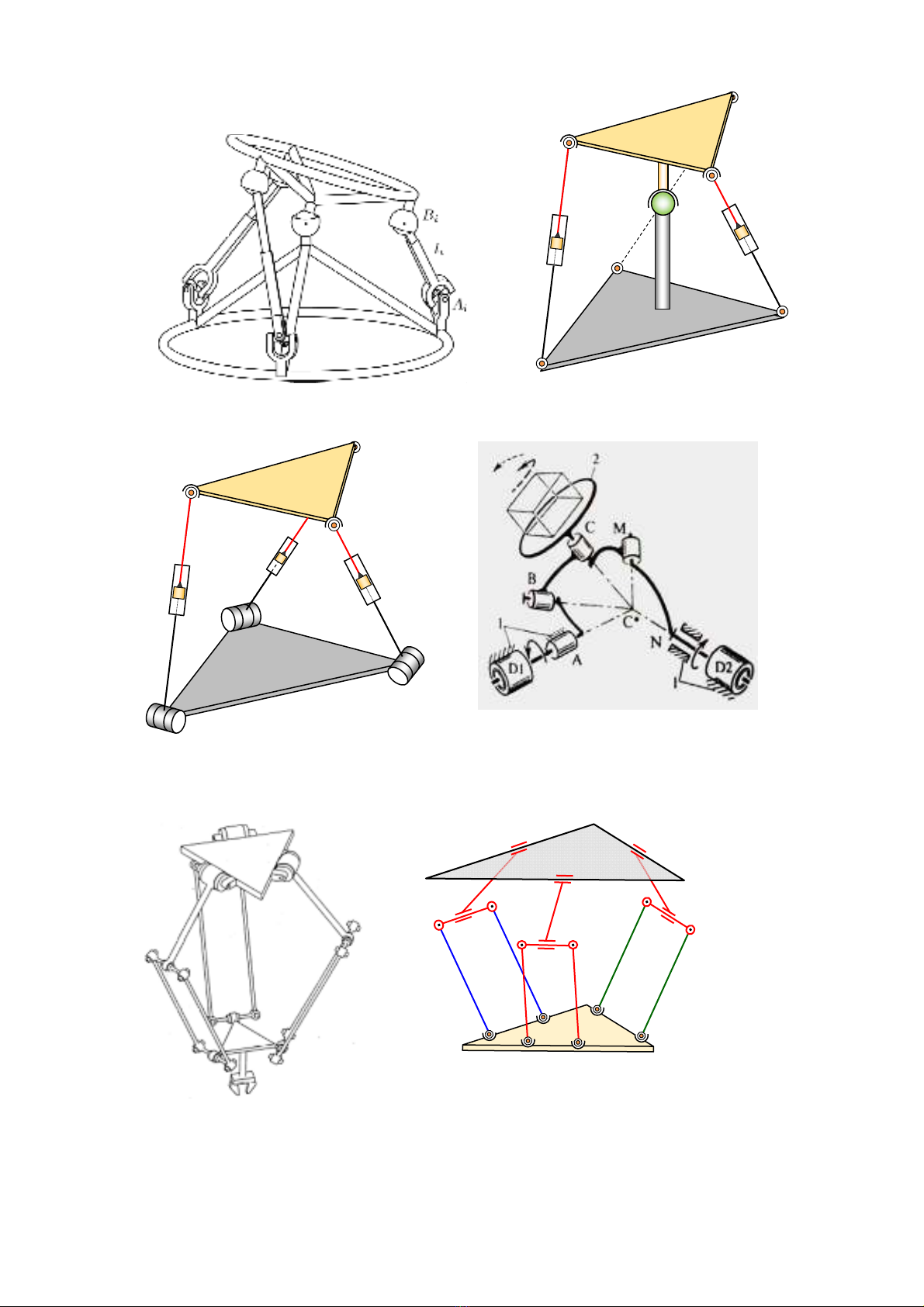
H. bài Robot Delta không gian
Bàn cố định
Bàn động S
R
R
R
Cơ cấu
hình bình
hành
S
R
R
Bàn cố định
P
P
P
R
S
S
S
Bàn động
3 DOF Stewart Platform
3 DOF Stewart Platform
S
S
S
Bàn cố định
P
P
P
S
S
S
S
Bàn động
S
P
U
S 3 chân SPS
3 chân UPS
Bàn động
Tay máy song song cầu