Bài tập Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 1
Chương 2: Biến đổi Fourier
P2.1: Dùng bảng tra và các tính chất
của biến đổi Fourier, tính F(ω) :
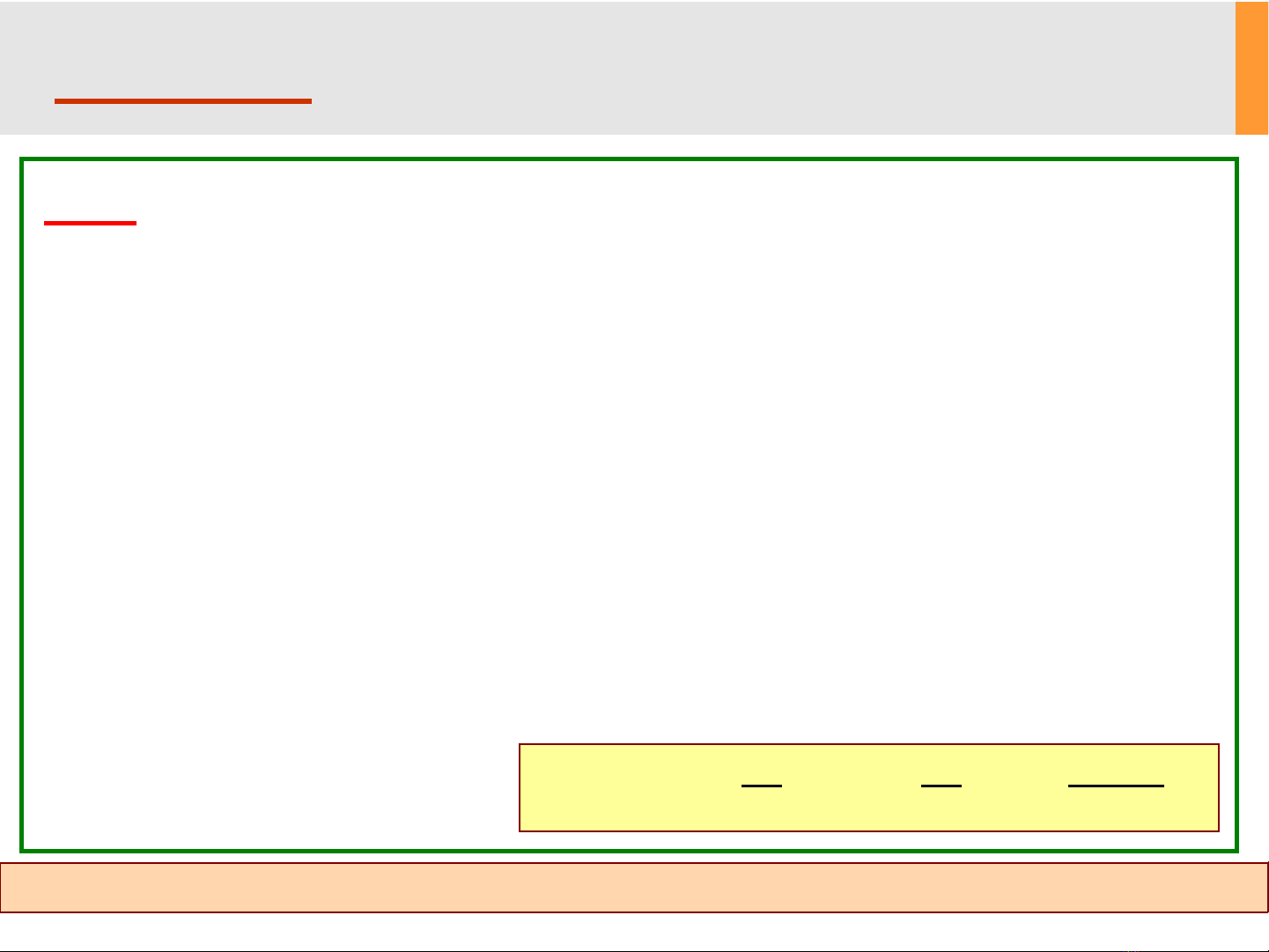
(a) f(t) =u(t – 1 ) – u(t – 2)
(b) f(t) = 4δ(t + 2)
(c) f(t) = e–4tu(t)
(d) f(t) = e–4tu(t – 2)
(e) f(t) = 2cos2(t)
ω 2ω
8
ee
jω
i2ω
1
(4ω)
ei2ω
(4 iω)
( (a)
(b) 4e
(c)
(d) e
(e) 2 ( )
( 2)
( 2) )
Ans:
ii
i
πδ ω
πδ ω
πδ ω
−−
−
−
+
−
+
+−
++
Bài tập Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 2
Chương 2: Biến đổi Fourier
2
2Aω1
ω2
(a iω)
( a) i [1 cos ] b) A)ns:
τ
+
−−
P2.2: Dùng định nghĩa biến đổi Fourier, xác định F(ω)cho các
tín hiệu :
A ( / 2 0)
f(t) A (0 / 2)
0 (
a
)
)
t
t
elsewhere
τ
τ
− − <<
= <<
at
0 ( 0)
f(t) te (0 );
b) a0
t
t
−
<
=<>
Bài tập Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 3
Chương 2: Biến đổi Fourier
sin(ωτ/2)
m(ωτ/2)
Ans:( Eτ )
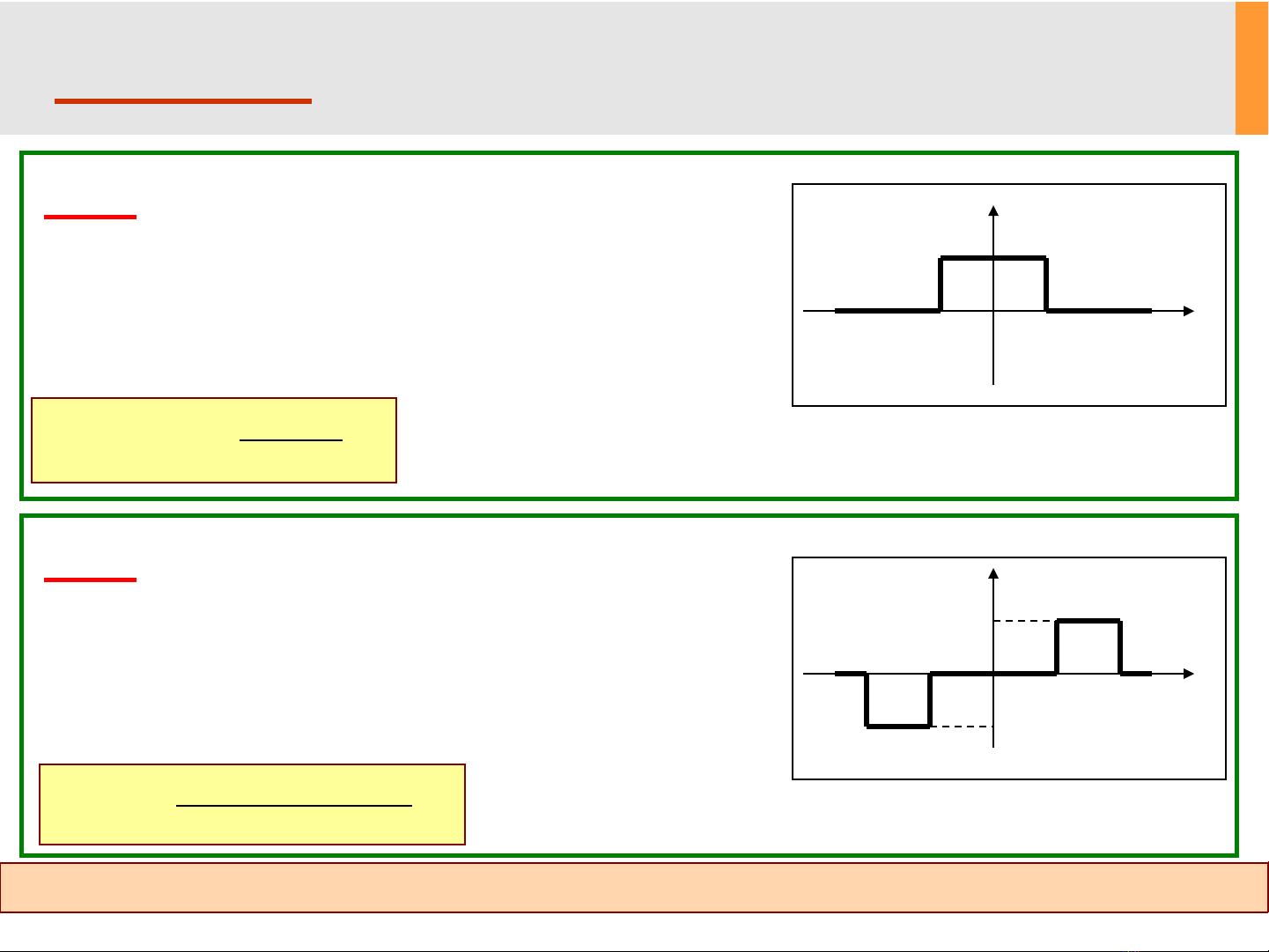
P2.3: Dùng định nghĩa biến đổi Fourier
và cách biểu diễn tín hiệu không tuần
hoàn thành tổng các hàm xung đơn vị,
xác định F(ω) ?
e(t)
Em
–τ/2 0τ/2 t
20[cos(2ω) cos(4ω)]
iω
(Ans: )
−
e(t)
0
t(s)
2 4
- 2- 4
10
-10
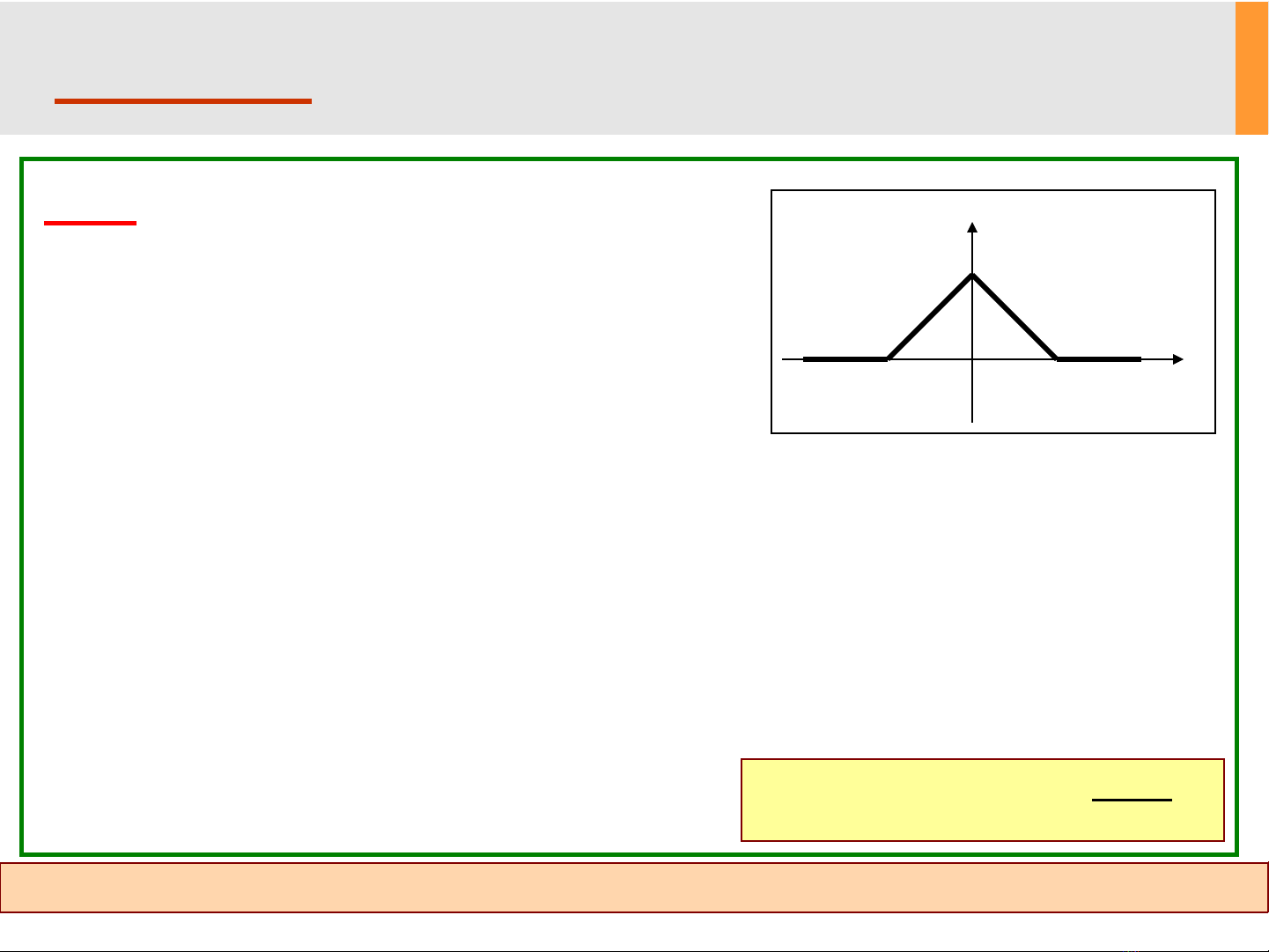
P2.4: Dùng định nghĩa biến đổi Fourier
và cách biểu diễn tín hiệu không tuần
hoàn thành tổng các hàm xung đơn vị,
xác định F(ω) ?
Bài tập Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 4
Chương 2: Biến đổi Fourier
( )
2
1 cos
ω
( (c) F(Ans ω2:) )
ω
−
=
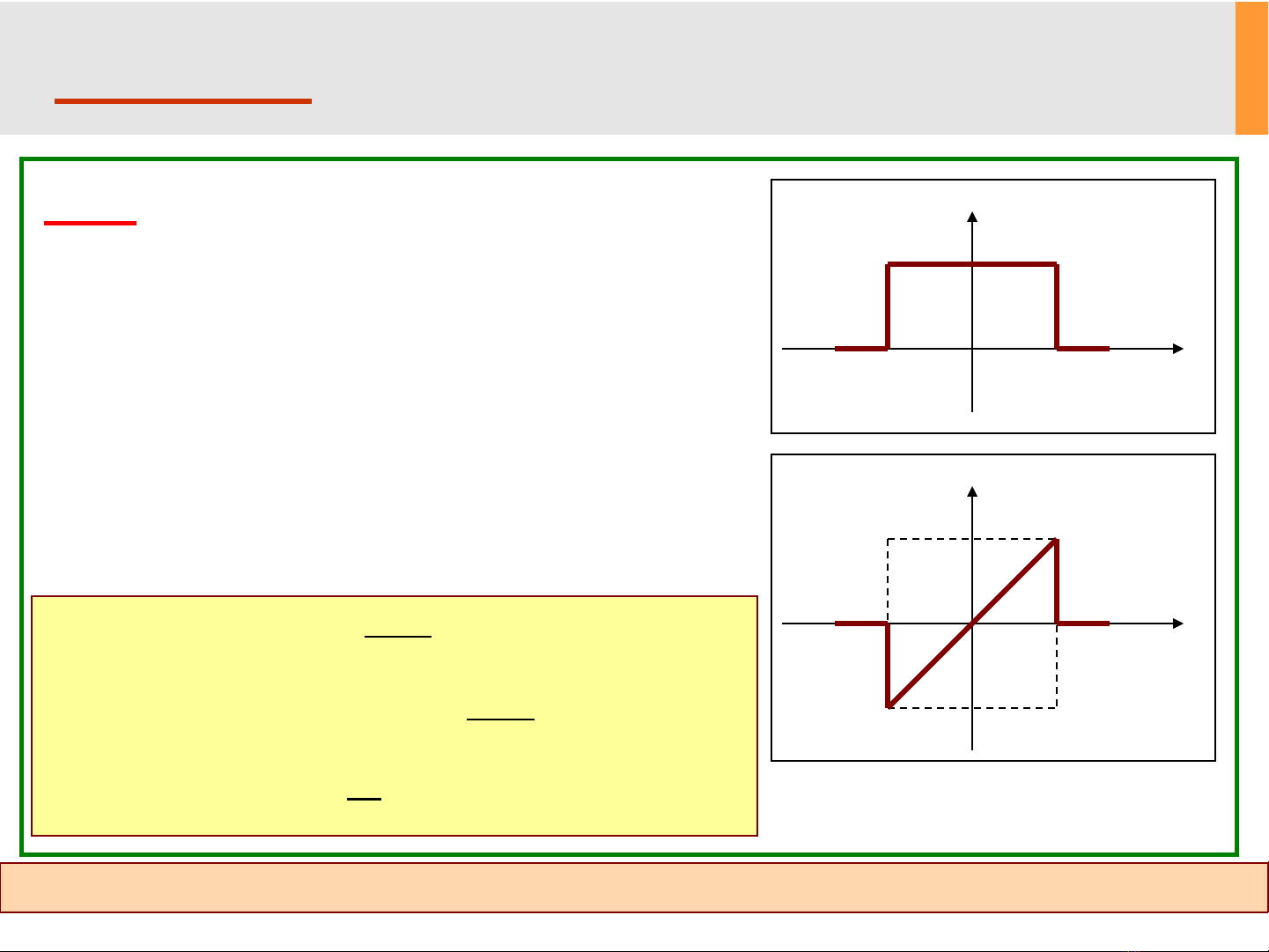
P2.5: Cho tín hiệu f(t) như hình vẽ.f(t)
1
1
–1
t(s)
0
a) Xác định f’(t) ?
b) Tìm biến đổi Fourier của f’(t) ?
c) Suy ra F(ω) = F{f(t)} ?
Bài tập Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 5
Chương 2: Biến đổi Fourier
( )
( )
( )
2
sin 2
1ω
sin 2
ω
i
2ω
( (a) F (ω)
(b) 2 cos(2 )
(c) F (ω) 2 cos 2 sin 2 )
Ans:
ω
ω
ω
ωω ω
=
−+
= −
P2.6: Cho 2tín hiệu như hình vẽ.
a) Xác định F{f1(t)} ?
b) Tìm f2’(t) và biến đổi
Fourier của nó ?
c) Suy ra F2(ω) = F{f2(t)} ?
f1(t)
0,5
2
–2
t(s)
0
f2(t)
1
2
–2
t(s)
0
-1