Sö dông Kü thuËt M« pháng Monter Carlo
trong viÖc ®Þnh gi¸ c«ng tr×nh x©y dùng
th.s TrÞnh thuú anh
Bé m«n Qu¶n trÞ kinh doanh
Khoa VËn t¶i – Kinh tÕ
Tr−êng §¹i häc Giao th«ng VËn t¶i
Tãm t¾t: X¸c ®Þnh gi¸ c«ng tr×nh x©y dùng lμ mét viÖc lμm khã kh¨n. M« pháng Monter
Carlo lμ mét kü thuËt m« pháng rÊt cã Ých trong viÖc −íc tÝnh gi¸ c¶ c«ng tr×nh. M« pháng nμy lμ
h÷u Ých vμ ®ang ®−îc ¸p dông réng r·i trong ph©n tÝch rñi ro chi phÝ dù ¸n ë c¸c n−íc ph¸t
triÓn. Bμi b¸o nμy nh»m t×m hiÓu c¸c vÊn ®Ò vÒ gi¸ c«ng tr×nh, giíi thiÖu m« pháng Monter
Carlo trong ph©n tÝch rñi ro, trªn c¬ së ®ã ®−a ra ph−¬ng ph¸p vμ tr×nh tù ¸p dông m« pháng
Monter Carlo trong x¸c ®Þnh gi¸ c«ng tr×nh.
Summary: Estimation of construction price is complicated. Monter Carlo simulation is an
useful technique in estimating the price of a construction project. This simulation is useful and
are widely applied on risk analysis of the cost of project in developed countries. This paper
aims to identify problems related to construction cost and to introduce Monter Carlo simulation
to apply in risk analysis. Base on these, method and process on Monter Carlo simulation to
estimate construction price are proposed.
CT 2
1. Giíi thiÖu chung
Gi¸ c¶ cña mét c«ng tr×nh x©y dùng lµ sù kÕt hîp gi÷a c¸i gi¸ mµ kh¸ch hµng (chñ ®Çu t−)
s½n lßng chi tr¶ vµ møc gi¸ mµ nhµ thÇu chÊp nhËn thùc hiÖn c«ng tr×nh víi mét tØ lÖ lîi nhuËn
nhÊt ®Þnh. Gi¸ c¶ ph¶i n»m trong mét tËp hîp c¸c møc gi¸ tèi ®a, tèi thiÓu vµ møc gi¸ phæ biÕn.
Kh¸ch hµng th−êng cho r»ng viÖc −íc tÝnh gi¸ c¶ ®¬n thuÇn ®−îc thùc hiÖn ë giai ®o¹n thiÕt kÕ
cña mét c«ng tr×nh x©y dùng, trong ®iÒu kiÖn b×nh th−êng, lµ møc gi¸ phæ biÕn nhÊt. Tuy nhiªn,
do thiÕu c¸c biÖn ph¸p ®iÒu chØnh nªn th−êng dÉn ®Õn kh¶ n¨ng lµ møc gi¸ nhµ thÇu ®−a ra sÏ
hoÆc cao h¬n hoÆc thÊp h¬n møc gi¸ −íc tÝnh.
Râ rµng viÖc −íc tÝnh gi¸ c¶ ®¬n thuÇn chØ lµ −íc tÝnh gi¸ thÇu mµ th«i. Tuy nhiªn kh¸ch
hµng lu«n tù tin r»ng møc gi¸ hä −íc tÝnh lµ kh«ng qu¸ l¹c quan vµ còng kh«ng qu¸ bi quan, mµ
®ã lµ møc gi¸ phæ biÕn nhÊt. NÕu nh− gi¸ c«ng tr×nh ®−îc −íc tÝnh mét c¸ch qu¸ thÊp, th× kh¸ch
hµng sÏ l·ng phÝ thêi gian vµ nguån lùc ®Ó lËp kÕ ho¹ch thùc hiÖn trong khi ®ã nã l¹i kh«ng thùc
tÕ v× nhµ thÇu kh«ng thÓ chÊp nhËn ®−îc møc gi¸ nµy. Ng−îc l¹i, nÕu gi¸ c«ng tr×nh ®−îc dù
tÝnh mét c¸ch qu¸ cao, th× sÏ lµm l·ng phÝ vèn ®Çu t−, còng nh− ¶nh h−ëng ®Õn c¸c ho¹t ®éng
kinh tÕ kh¸c.
Môc tiªu cña bµi b¸o nµy lµ ®−a ra mét c«ng cô, ®ã chÝnh lµ ph©n bè x¸c suÊt mµ nhê ®ã
ng−êi ta dù kiÕn ®−îc gi¸ c¶ c«ng tr×nh. Kh¸ch hµng còng nh− nhµ t− vÊn ®Òu cã thÓ sö dông
nã ®Ó dù ®o¸n gi¸ c¶ mét c«ng tr×nh cô thÓ. Ph−¬ng ph¸p nµy cã thÓ ®−îc øng dông ë bÊt cø
giai ®o¹n nµo ®Ó −íc tÝnh gi¸ c«ng tr×nh, tuy nhiªn, chóng ®−îc øng dông phæ biÕn ®Ó tÝnh gi¸
trong giai ®o¹n lËp thiÕt kÕ.
BÊt tr¾c ¶nh h−ëng nhiÒu ®Õn viÖc −íc tÝnh gi¸ c¶. Gi¸ c¶ kh«ng ph¶i chØ ®−îc x¸c ®Þnh
trªn c¬ së khoa häc chÝnh x¸c, kh¸ch quan, mµ cßn ®−îc c¨n cø trªn trùc gi¸c còng nh− tr×nh
®é cña nh÷ng ng−êi thùc hiÖn. Do vËy cã nh÷ng chªnh lÖch gi÷a c¸c −íc ®o¸n. ViÖc dù ®o¸n
gi¸ c¶ c«ng tr×nh x©y dùng lµ tæng hîp cña nhiÒu phÇn bé phËn, vµ cã thÓ ®−îc hç trî bëi c«ng
cô thèng kª. Lý thuyÕt x¸c suÊt cho phÐp thÓ hiÖn c¸c bÊt tr¾c t−¬ng lai th«ng qua c¸c con sè
cô thÓ, v× vËy kh¶ n¨ng kh¸c biÖt gi÷a c¸c sù kiÖn cã thÓ so s¸nh trùc tiÕp víi nhau ®−îc. Th«ng
tin vÒ x¸c suÊt cña sù kiÖn t−¬ng lai hoÆc mét ®iÒu kiÖn nµo ®ã tån t¹i th−êng ®−îc thÓ hiÖn
trong hµm mËt ®é x¸c suÊt. V× vËy nÕu chóng ta cã thÓ x¸c ®Þnh ®−îc mét sè hµm mËt ®é x¸c
suÊt ®Ó dù kiÕn gi¸ c¶ c«ng tr×nh x©y dùng th× chóng ta cã thÓ kiÓm tra kh¶ n¨ng −íc tÝnh ®ã lµ
sai lÖch hay kh«ng.
¦íc tÝnh gi¸ c¶: c¸c vÊn ®Ò thùc tÕ hiÖn nay
Khi −íc tÝnh gi¸ mét c«ng tr×nh x©y dùng trong giai ®o¹n lËp dù ¸n, chóng ta th−êng nh×n
vµo c¸c dù ¸n ®· lµm trong qu¸ khø ®Ó tham kh¶o c¬ së d÷ liÖu vµ ®iÒu chØnh chóng cho dù ¸n
hiÖn t¹i. ViÖc dù b¸o gi¸ c¶ c«ng tr×nh x©y dùng th−êng ®−îc ®Æt trªn c¬ së ph©n tÝch mét sè
c¸c dù ¸n trong qu¸ khø cã tÝnh chÊt t−¬ng tù víi dù ¸n ®ang tiÕn hµnh nh»m ph©n tÝch chi phÝ
vµ c¬ cÊu chi phÝ cña chóng. Ng−êi ta gi¶ thiÕt r»ng gi¸ thÇu cña mét h¹ng môc cÇn ®−îc x©y
dùng trong t−¬ng lai cã thÓ ®−îc x¸c ®Þnh th«ng qua viÖc ph©n tÝch vµ ®iÒu chØnh gi¸ thÇu cña
c¸c h¹ng môc t−¬ng tù ®· ®−îc thùc hiÖn trong qu¸ khø.
Trong mét sè tr−êng hîp, khi kh«ng cã d÷ liÖu chi phÝ cã s½n, th× kinh nghiÖm vµ kü n¨ng
®ãng vai trß quan träng trong viÖc thu thËp th«ng tin nh»m dù ®o¸n gi¸ c¶. NhiÒu nh©n tè t¸c
®éng tíi kh¶ n¨ng dù ®o¸n gi¸ c¶, nh− ph¹m vi cña c¸c th«ng tin thiÕt kÕ cã s½n (mËp mê trong
thiÕt kÕ vµ tÝnh to¸n, ph−¬ng ph¸p tÝnh kh«ng râ rµng); c¸c sè liÖu cã s½n liªn quan ®Õn lo¹i dù
¸n trong ®iÒu kiÖn cô thÓ; tÝnh t−¬ng tù cña lo¹i h×nh dù ¸n ®ang thùc hiÖn vµ c¸c dù ¸n tr−íc
®©y.
CT 2
Chóng ta sÏ xem xÐt c¸c ®iÓm nµy mét c¸ch chi tiÕt, nh−ng còng cÇn chó ý lµ gi¸ c¶ ®−îc
sö dông trong dù ®o¸n chØ cã thÓ ®¹t ®−îc møc chÝnh x¸c nh− nã ®· ®−îc x¸c ®Þnh trong c¸c dù
¸n mÉu. H¬n n÷a, c¸i tèt nhÊt cña tËp hîp mÉu dù ¸n nghiªn cøu lµ mét kh¸i niÖm hai mÆt. VÒ
mÆt nguyªn t¾c, mÉu cÇn ®−îc lÊy cµng nhiÒu cµng tèt. MÆt kh¸c, cÇn nhí r»ng mÉu chØ lÊy víi
c¸c dù ¸n x©y dùng t−¬ng tù víi dù ¸n ®ang lËp. Nãi c¸ch kh¸c, mÉu nªn ®ång nhÊt ®Ó cã thÓ
nghiªn cøu c¸c ®Æc ®iÓm chi phÝ chÝnh cña dù ¸n.
Ng−êi ta còng cho r»ng nÕu nh− c¸c d÷ kiÖn gi¸ c¶ trong qu¸ khø ®−îc x¸c ®Þnh tõ nhiÒu
dù ¸n x©y dùng h¬n lµ tõ mét dù ¸n, th× møc ®é tin cËy sÏ cao h¬n, mÆc dï nh− vËy cã nghÜa lµ
ph¶i chÊp nhËn nhiÒu so s¸nh. Khi c¸c d÷ liÖu lµ cã h¹n, ph¶i c©n ®èi gi÷a quy m« mÉu vµ tÝnh
®ång nhÊt cña mÉu. Tuy nhiªn kh«ng thÓ x¸c ®Þnh chÝnh x¸c thÕ nµo lµ c©n ®èi, nh−ng khi cã
nhiÒu bÊt tr¾c, sè mÉu h¹n chÕ (ch¼ng h¹n d−íi 5 mÉu) lµ hîp lý.
Kh¸i niÖm "cÈn thËn" kh«ng cã nghÜa g× hÕt c¶. Th«ng tin cÇn lµ gi¸ thanh to¸n cuèi cïng
khi dù ¸n hoµn tÊt. Th−êng d÷ liÖu chi phÝ liªn quan ®Õn c¸c ph©n tÝch vÒ gi¸ thÇu lu«n cho thÊy
t¸c ®éng cña c¸c chªnh lÖch khu vùc trong gi¸ x©y dùng vµ kh¸c biÖt ®èi víi quy m«, chÊt
l−îng, tÝnh phøc t¹p, vµ kh¶ n¨ng x©y dùng cña c¸c dù ¸n. Do vËy, kü n¨ng vµ c¸c ®¸nh gi¸
chuyªn nghiÖp lµ cùc kú cÇn thiÕt trong tr−êng hîp lùa chän c¸c dù ¸n t−¬ng tù ®èi víi dù ¸n
®−îc ®Ò suÊt.
2. X¸c ®Þnh gi¸ c«ng tr×nh vμ ph©n tÝch rñi ro
Mét ®iÓm kh¸c cÇn ph¶i xem xÐt lµ sù ®éc lËp cña c¸c h¹ng môc chÝnh ®−îc sö dông trong
khi lËp kÕ ho¹ch chi phÝ. Nghiªn cøu cho thÊy c¸c h¹ng môc chÝnh kh«ng cã mèi quan hÖ t¸c
®éng lÉn nhau. BÊt cø ch−¬ng tr×nh ph©n tÝch rñi ro nµo còng ®Òu kh«ng tÝnh ®Õn c¸c h¹ng môc
®éc lËp nµy, hoÆc kh«ng kiÓm ®Þnh c¸c hÖ sè t¸c ®éng ®ã. ChØ cã mét c¸ch thùc sù h÷u hiÖu lµ
ph¶i xem xÐt l¹i sè liÖu mét c¸ch cÈn thËn, nhê ®ã cã thÓ tr¸nh ®−îc sai sãt cña bÊt cø kü thuËt
nµo sö dông sè liÖu qu¸ khø ®Ó x¸c ®Þnh chi phÝ. Cã nhiÒu kü thuËt kh¸c nhau ®−îc sö dông
trong giai ®o¹n thiÕt kÕ nh»m −íc tÝnh chi phÝ x©y dùng c«ng tr×nh.
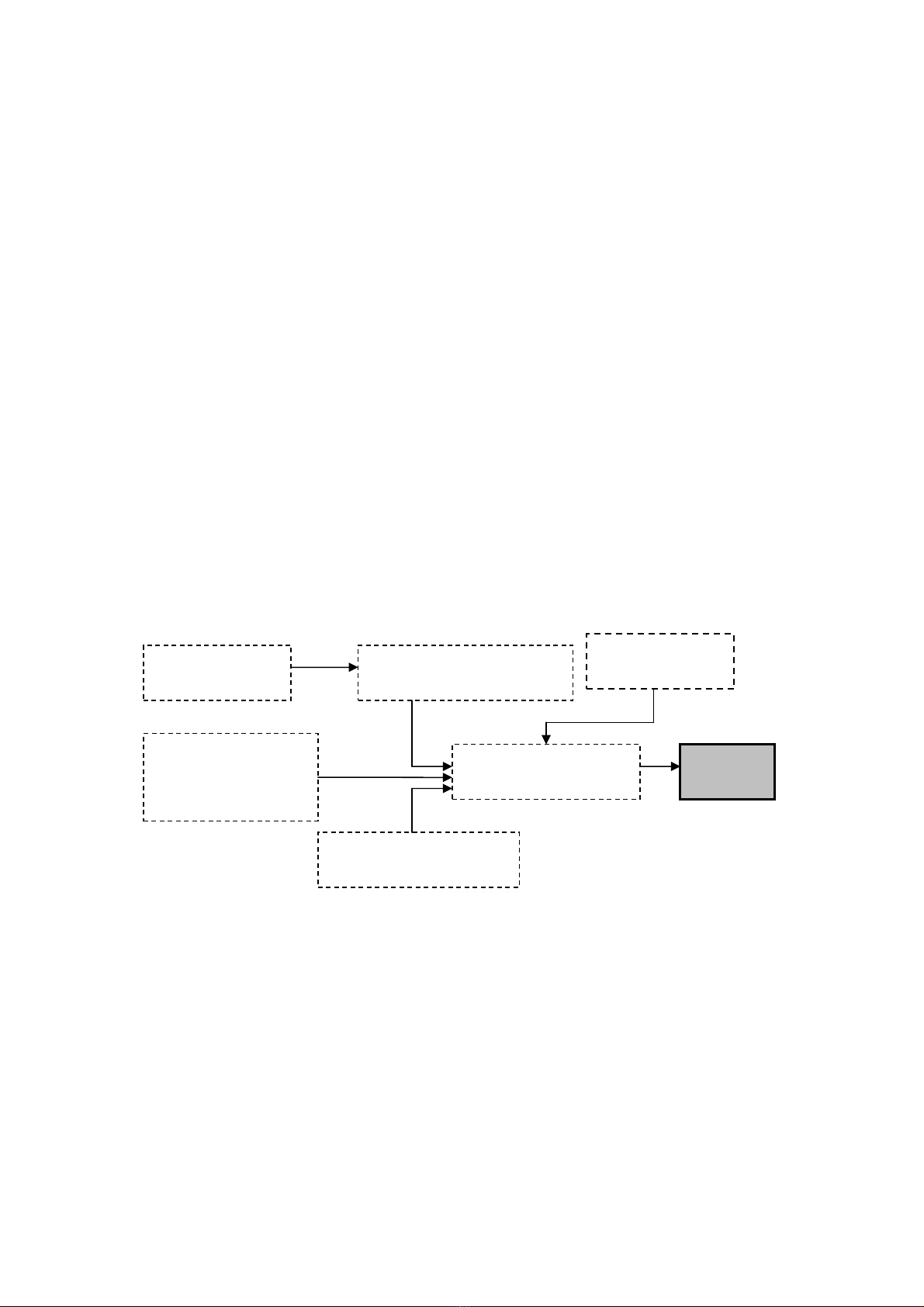
H×nh 1 cho thÊy qu¸ tr×nh lËp gi¸ bá thÇu. Khèi l−îng cña mçi lo¹i h¹ng môc ®−îc x¸c ®Þnh
vµ tËp hîp mÉu trong qu¸ khø ®−îc sö dông ®Ó tÝnh gi¸ bá thÇu ®¬n vÞ. Gi¸ bá thÇu ®¬n vÞ ®−îc
tÝnh to¸n cho mçi h¹ng môc chÝnh ®−îc nh©n víi khèi l−îng c¸c h¹ng môc ®ã sÏ x¸c ®Þnh ®−îc
gi¸ dù thÇu cuèi cïng.
Gi¸ bá thÇu ®¬n vÞ trung b×nh thÓ hiÖn trung b×nh cña mÉu theo hµm ph©n phèi x¸c suÊt
®−îc x¸c ®Þnh trªn c¬ së tËp hîp c¸c chi phÝ qu¸ khø kh¸c nhau hoÆc c¸c d÷ liÖu gi¸ c¶ kh¸c
nhau. TÊt nhiªn, ng−êi ta còng dù kiÕn r»ng cã mét sè thay ®æi dao ®éng ®èi víi gi¸ bá thÇu ®¬n
vÞ trung b×nh, nh−ng tæng gi¸ dù kiÕn ph¶i lµ mét gi¸ trÞ n»m ®©u ®ã trong tËp hîp mÉu.
C¸c dù ¸n trong
qu¸ khø
§iÒu chØnh cã tÝnh ®Õn yÕu tè
thêi gian vµ chÊt l−îng
Gi¶ thiÕt vÒ dù ¸n
®−îc ®Ò xuÊt
C¸c th«ng tin hiÖn t¹i
®−îc thu thËp tõ phÝa
c¸c chuyªn gia vµ c¸c
nhµ cung cÊp
Dù ¸n ®Ò xuÊt (th«ng tin
®Þnh tÝnh vµ ®Þnh l−îng) KÕ ho¹ch
chi phÝ
Dù ®o¸n vÒ l¹m ph¸t vµ chi
phÝ lao ®éng t−¬ng lai
CT 2
H×nh 1. S¬ ®å qu¸ tr×nh x¸c ®Þnh gi¸ dù thÇu
Nãi c¸ch kh¸c, khi mçi gi¸ bá thÇu ®¬n vÞ ®−îc x¸c ®Þnh tõ hµm ph©n phèi x¸c suÊt, th× dù
b¸o tæng thÓ còng lµ mét bé phËn trong hµm ph©n phèi x¸c suÊt, ®Æc ®iÓm cña mçi d¹ng hµm
®−îc x¸c ®Þnh bëi ®Æc ®iÓm cña ph©n phèi c¸ nh©n ®èi víi mçi lo¹i h¹ng môc chÝnh. Sö dông
ph©n tÝch d−íi ®©y, cã thÓ ®èi víi ph©n phèi x¸c suÊt phï hîp cho toµn bé qu¸ tr×nh dù b¸o ®Ó
x¸c ®Þnh ®Æc ®iÓm cña tËp hîp cÇn x¸c ®Þnh. Nãi tãm l¹i lµ cÇn x¸c ®Þnh:
- X¸c suÊt mµ gi¸ thÇu do nhµ thÇu ®−a ra sÏ kh«ng v−ît qu¸ møc ®−îc dù b¸o
- Kho¶ng biÕn thiªn mµ møc gi¸ cña nhµ thÇu n»m trong ®ã.
2.1. Ph©n tÝch rñi ro sö dông x¸c suÊt
Khi cã th«ng tin trong giai ®o¹n thiÕt kÕ, ng−êi ta cã thÓ tÝnh ®Õn nhiÒu rñi ro kh¸c nhau vµ
¶nh h−ëng cña nã ®Õn gi¸ c«ng tr×nh. Tuy vËy, mét sè rñi ro kh«ng thÓ ®−îc x¸c ®Þnh mét c¸ch
ch¾c ch¾n ë giai ®o¹n thiÕt kÕ, ch¼ng h¹n nh− ®iÒu kiÖn thêi tiÕt kh¾c nghiÖt thÊt th−êng sÏ t¸c
®éng ®Õn chi phÝ dù ¸n. Mét sè lín rñi ro ph¸t sinh do thiÕu th«ng tin, vÝ dô nh−, thiÕt kÕ kh«ng
phï hîp vµ thiÕu mét sè th«ng tin nhÊt ®Þnh ë giai ®o¹n ®Çu trong qu¸ tr×nh thiÕt kÕ.
H−íng gi¶i quyÕt lµ x¸c ®Þnh møc rñi ro cho phÐp ®èi víi mét tËp hîp c¸c h¹ng môc vµ
ph©n bæ mçi h¹ng môc víi x¸c suÊt cña mçi sù kiÖn xuÊt hiÖn vµ ®−a ra 3 møc gi¸ dù kiÕn: møc
gi¸ phæ biÕn, gi¸ thÊp nhÊt vµ gi¸ cao nhÊt.
2.2. Sö dông m« pháng Monter Carlo trong ph©n tÝch rñi ro
Chóng ta ®· sö dông kÕ ho¹ch lËp gi¸ theo h¹ng môc nh»m nghiªn cøu vÒ ph©n tÝch rñi ro.
Ngoµi ra còng cã thÓ øng dông ®Ó dù b¸o vµ tÝnh to¸n thêi gian x©y dùng ®èi víi c¸c ho¹t ®éng
vµ tæng thêi gian.
Ph©n tÝch rñi ro th−êng x¸c ®Þnh vÒ mÆt lý thuyÕt chØ sè gi¸ ®¬n vÞ trung b×nh ®èi víi mçi
lo¹i c«ng viÖc n»m trong kÕ ho¹ch chi phÝ cña c«ng tr×nh x©y dùng. ChØ sè lý thuyÕt nµy ®−îc
x¸c ®Þnh c¨n cø vµo ph©n bè x¸c suÊt víi cïng ®Æc ®iÓm thèng kª, nghÜa lµ hµm mËt ®é x¸c
suÊt, còng nh− ®Æc ®iÓm cña c¬ së d÷ liÖu gèc mµ tõ ®ã chØ sè gi¸ ®¬n vÞ trung b×nh ®−îc tÝnh
to¸n. ChØ sè gi¸ lý thuyÕt th−êng ®−îc sö dông ®Ó x¸c ®Þnh tæng gi¸ dù kiÕn cho c«ng tr×nh x©y
dùng. NÕu bµi tËp nµy ®−îc lÆp l¹i víi sè lÇn ®ñ lín, th× cã thÓ thÊy d¹ng hµm mËt ®é x¸c suÊt
x¸c ®Þnh tæng gi¸, vµ do vËy x¸c ®Þnh tæng chi phÝ phæ biÕn nhÊt.
CT 2 3. Xem xÐt mét sè hμm ph©n phèi x¸c suÊt ¸p dông trong ph©n tÝch gi¸
c«ng tr×nh
Qu¸ tr×nh lùa chän d¹ng hµm ph©n phèi x¸c suÊt nh×n chung lµ kh¸ khã kh¨n. §Ó lùa chän
d¹ng hµm ph©n phèi x¸c suÊt ®óng ph¶i tu©n theo mét sè nguyªn t¾c nhÊt ®Þnh. §Çu tiªn ta
ph¶i liÖt kª mäi thø vÒ biÕn sè, sau ®ã nghiªn cøu c¸c m« h×nh ph©n bè x¸c suÊt c¬ b¶n, trªn c¬
së ®ã lùa chän d¹ng hµm ph©n bè x¸c suÊt phï hîp víi ®Æc ®iÓm cña biÕn sè theo ®iÒu kiÖn
xem xÐt.
C¸c tham sè sau ®©y ®−îc sö dông cho qu¸ tr×nh ph©n tÝch:
- Sè trung b×nh lµ sè ®−îc sö dông nhiÒu nhÊt trong nghiªn cøu thèng kª, sè trung b×nh lo¹i
bá c¸c gi¸ trÞ qu¸ thÊp hoÆc qu¸ cao th−êng kh«ng ®¹i diÖn cho tËp hîp sè liÖu.
- Sè trung vÞ, lµ l−îng biÕn cña ®¬n vÞ ®øng ë vÞ trÝ chÝnh gi÷a trong d·y sè, chia sè ®¬n vÞ
trong d·y sè thµnh hai phÇn b»ng nhau.
- Mèt lµ gi¸ trÞ xuÊt hiÖn nhiÒu nhÊt trong d·y sè, mèt lu«n ë vÞ trÝ cao nhÊt víi bÊt cø h×nh
d¹ng nµo cña ph©n bè x¸c suÊt.
- §é lÖch chuÈn lµ c¨n bËc hai cña ph−¬ng sai
- Ph−¬ng sai lµ trung b×nh céng cña b×nh ph−¬ng c¸c ®é lÖch gi÷a l−îng biÕn víi sè trung
b×nh cña c¸c l−îng biÕn ®ã.
Ph©n phèi cã thÓ lµ rêi r¹c hoÆc liªn tôc. PhÇn lín c¸c ho¹t ®éng c«ng nghÖ x©y dùng lµ
ph©n phèi liªn tôc víi gi¸ trÞ t¨ng trong mét kho¶ng biÕn thiªn nhÊt ®Þnh. Ph©n phèi rêi r¹c liªn
quan ®Õn c¸c gi¸ trÞ cô thÓ n»m trong kho¶ng biÕn thiªn.
C¸c d¹ng hµm ph©n phèi x¸c suÊt th«ng th−êng bao gåm ph©n phèi ®Òu (Uniform), ph©n
phèi Triangular, ph©n phèi chuÈn
(Normal), ph©n phèi Poisson, ph©n
phèi nhÞ thøc (Binomial), ph©n phèi
Longormal, ph©n phèi mò
(Exponential), ph©n phèi h×nh häc
(Geometric), ph©n phèi siªu h×nh häc
(Hypergeometric), ph©n phèi Weibull,
ph©n phèi Beta.
CT 2
ViÖc lùa chän ph©n phèi phï hîp
cho ph©n tÝch lµ rÊt quan träng, sau
®©y sÏ nghiªn cøu bèn ph©n phèi
th−êng ®−îc sö dông phæ biÕn h¬n c¶.
3.1. Ph©n phèi ®Òu
Trong ph©n phèi ®Òu tÊt c¶ c¸c
gi¸ trÞ n»m trong kho¶ng tèi thiÓu vµ
tèi ®a th−êng xuÊt hiÖn víi tÇn suÊt nh− nhau.
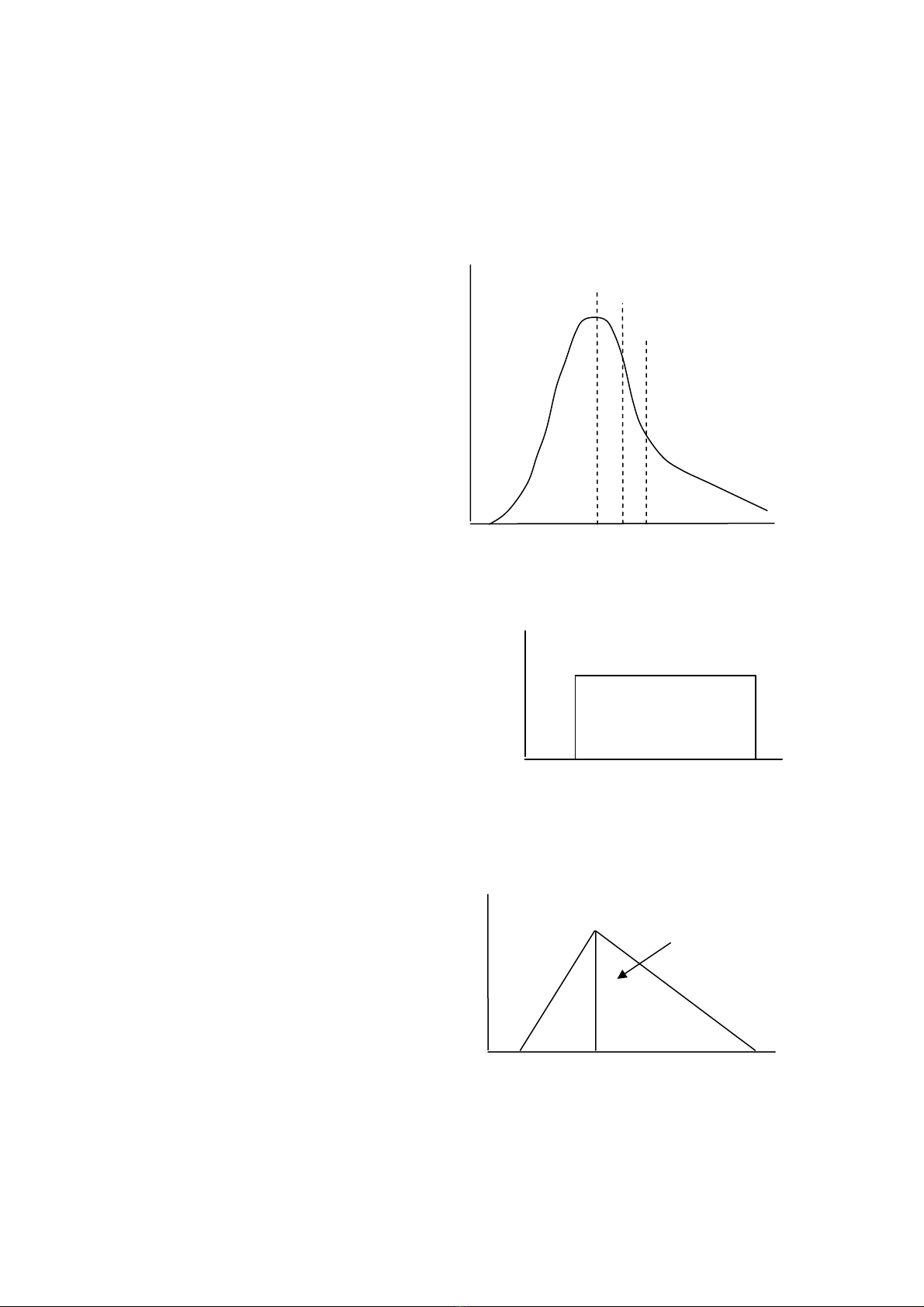
Trung vÞ
Trung b×nh
Mèt
MËt
®é
x¸c
suÊt
30 tuÇn 50 tuÇn 80 tuÇn
H×nh 2. Hμm ph©n phèi x¸c suÊt
Hµm x¸c suÊt:
P(1) = P(2) = … = P(n) = 1/n
Gi¸ trÞ trung b×nh: (n+1)/2
Ph−¬ng sai: (nP2 - 1)/12h
3.2. Ph©n phèi Triangular
Ph©n phèi Triangular m« t¶ mét t×nh
huèng mµ ng−êi ta cã thÓ x¸c ®Þnh c¸c gi¸ trÞ
tèi thiÓu, tèi ®a, vµ gi¸ trÞ phæ biÕn. C¸c gi¸ trÞ th−êng tËp trung quanh gi¸ trÞ phæ biÕn h¬n lµ gi¸
trÞ tèi thiÓu vµ tèi ®a. Ph©n phèi nµy th−êng ®−îc sö dông réng r·i v× nã dÔ sö dông. Tuy nhiªn
h¹n chÕ cña nã lµ kÐm chÝnh x¸c so víi c¸c
ph©n phèi x¸c suÊt kh¸c.
MËt
®é
x¸c
suÊt
Min Max
H×nh 3. Ph©n phèi ®Òu
Khu vùc nµy cho
thÊy kh¶ n¨ng gi¸
sÏ r¬i vµo kho¶ng
gi÷a gi¸ phæ biÕn
vµ gi¸ tèi ®a
min gi¸ trÞ phæ biÕn max
H×nh 4. Ph©n phèi Triangular
3.3. Ph©n phèi chuÈn
Ph©n phèi chuÈn lµ ph©n phèi ®−îc sö
dông nhiÒu nhÊt trong nghiªn cøu x¸c suÊt.
Ph©n phèi chuÈn cã d¹ng h×nh chu«ng, sö dông
hai tham sè lµ gi¸ trÞ trung b×nh vµ ®é lÖch
chuÈn. Ph©n phèi chuÈn cã thÓ sö dông khi cã
c¸c sè liÖu tin cËy vÒ gi¸ c«ng tr×nh x©y dùng.
H×nh 5 cho thÊy ph©n phèi chuÈn víi cïng gi¸ trÞ