ĐẠI HỌC BÁCH KHOA TPHCM
Khoa Khoa học ứng dụng-BM Toán ứng dụng
ĐỀ CHÍNH THỨC
(Đề gồm có 18 câu/4 trang)
ĐỀ THI GIỮA KÌ HK191
Môn: Giải tích 1
.Ngày thi : 17/11/2019
Giờ thi: CA 2 Mã đề thi 2000
Thời gian: 45 phút, không kể thời gian phát đề
Sinh viên không được sử dụng tài liệu
Câu 1. Một sợi dây kim loại dài 60 cm được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình
vuông cạnh a, đoạn dây thứ hai uốn thành đường tròn bán kính r. Để tổng diện tích của hình
vuông và hình tròn nhỏ nhất thì tỉ số a
rnào sau đây đúng?
A. 3. B. 2. C. Các câu khác sai. D. 4.
Câu 2. Gọi Ilà đoạn có độ dài lớn nhất sao cho f(x) = x3−6x2+ 9xgiảm trên đó. Độ dài khoảng I
bằng
A. 2.B. 4.C. 3.D. 1.
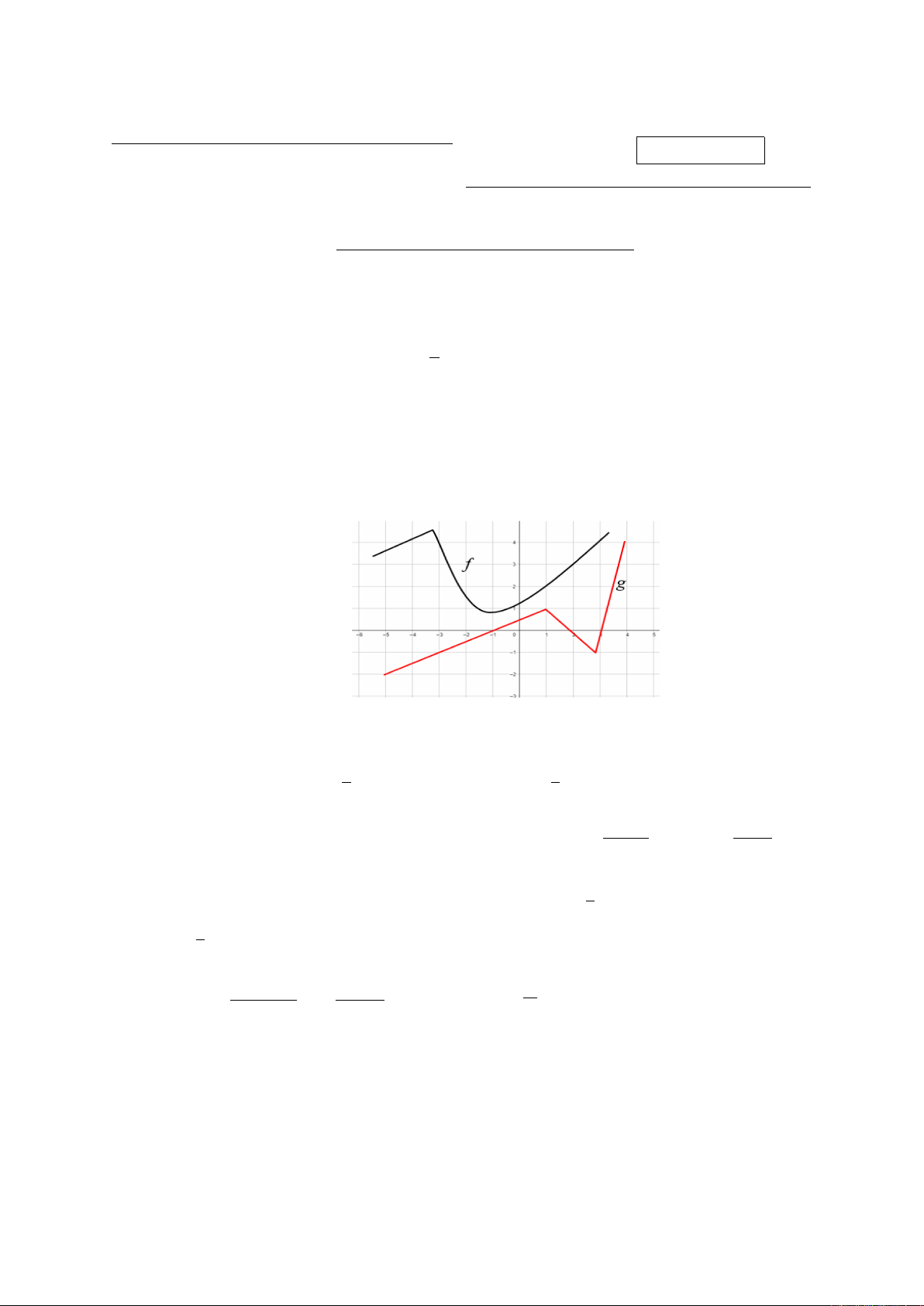
Câu 3. Cho hai hàm f(x)và g(x)có đồ thị như hình vẽ.
Đặt h(x) = f(x)−2g(x), giá trị của h0(−1) là
A. -1 B. 1
2C. −1
2D. 1
Câu 4. Cho đường cong xác định bởi phương trình tham số: x(t) = t
t2−9, y(t) = t2
t−3.
Khẳng định nào sau đây là đúng?
A. y= 0 là tiệm cận ngang. B. x=−1
2là tiệm cận đứng.
C. y=−3
2là tiệm cận ngang. D. Cả ba câu trên sai.
Câu 5. Khi x→0,sắp xếp các vô cùng bé sau theo thứ tự BẬC TĂNG DẦN:
α(x) = 3
√x9+ 2x7+4
√x2+ 1 −1, β(x) = 2√x3−1, γ(x) = tan x−sin x.
A. β, α, γ B. α, β, γ C. γ, α, β D. γ, β, α
Trang 1/4- Mã đề thi 2000
Câu 6. Để tính gần đúng diện tích miền giới hạn bởi đường cong
y= 9 −x2và trục hoành trên [0,3], người ta chia đoạn [0,3] trên trục Ox thành n phần bằng
nhau bởi các điểm xi=3i
n, i = 0,1,2, ..., n và tạo các hình chữ nhật có cùng chiều rộng là 3
n
như hình vẽ.
Diện tích cần tính được Sđược xấp xỉ bằng tổng diện tích các hình chữ nhật này. Tính giá trị
xấp xỉ nói trên.
A. Sn=3
n"9−3
n2
+9−23
n2
... +9−n3
n2#
B. Sn=9−3
n2
+9−23
n2
+... +9−n3
n2
C. Sn=3
n3
n+2.3
n+... +n.3
nD. Các câu khác SAI
Câu 7. Cho f(x) = x2g3
x+ 2, trong đó gkhả vi tại mọi điểm và g(3) = −4, g0(3) = 2.
Giá trị của f0(−1) là
A. 10 B. 2C. −10 D. 21
Câu 8. Số vụ tội phạm nghiêm trọng tại một thành phố lớn cho bởi hàm số
N(t) = −0.2t3+ 2.5t2+ 100 (0 ≤t≤7)
, trong đó ttính bằng năm và t= 0 là năm 2011. Tính N0(5) và cho biết ý nghĩa.
A. N0(5) = 10, năm 2016 số vụ tội phạm nghiêm trọng tăng 10 vụ/năm.
B. N0(5) = 10, năm 2006 có 10 vụ tội phạm nghiêm trọng.
C. N0(5) = 15, năm 2016 có thêm 15 vụ tội phạm nghiêm trọng.
D. Các câu khác sai.
Câu 9. Một gia đình dự định tổ chức tiệc thôi nôi ở một nhà hàng. Nhà hàng có mức phục vụ chung
cho một bữa tiệc là 5 triệu đồng (các chi phí địa điểm, phục vụ,... ) và giá cho mỗi khách ăn là
250.000 đồng. Gia đình dự tính chi phi tối đa là 25 triệu đồng. Goi xlà số khách mời và y(x)
là hàm chi phí cho bữa tiệc. Biết nhà hàng nhận đặt tiệc tối thiểu 2 bàn mỗi bàn 10 người. Tìm
miền xác định của hàm số y(x).
A. [20,50] B. [20,60] C. [20,80] D. [20,40]
Câu 10. Lượng khí ôxi có thể hòa tan trong nước phụ thuộc vào nhiệt độ của nước. Nồng độ S(mg/L)
của khí ôxi là một hàm số theo nhiệt độ T (oC), hỏi ý nghĩa và đơn vị của S0(T)là gì?
A. Là tốc độ thay đổi của nhiệt độ nước đối với nồng độ khí ôxi, đơn vị là oC/ (mg/L).
B. Là tốc độ thay đổi của nồng độ khí ôxi đối với nhiệt độ nước, đơn vị là (mg/L)/oC.
C. Là tốc độ thay đổi của nồng độ khí ôxi đối với nhiệt độ nước, đơn vị là oC/ (mg/L).
D. Các câu kia đều sai.
Trang 2/4- Mã đề thi 2000
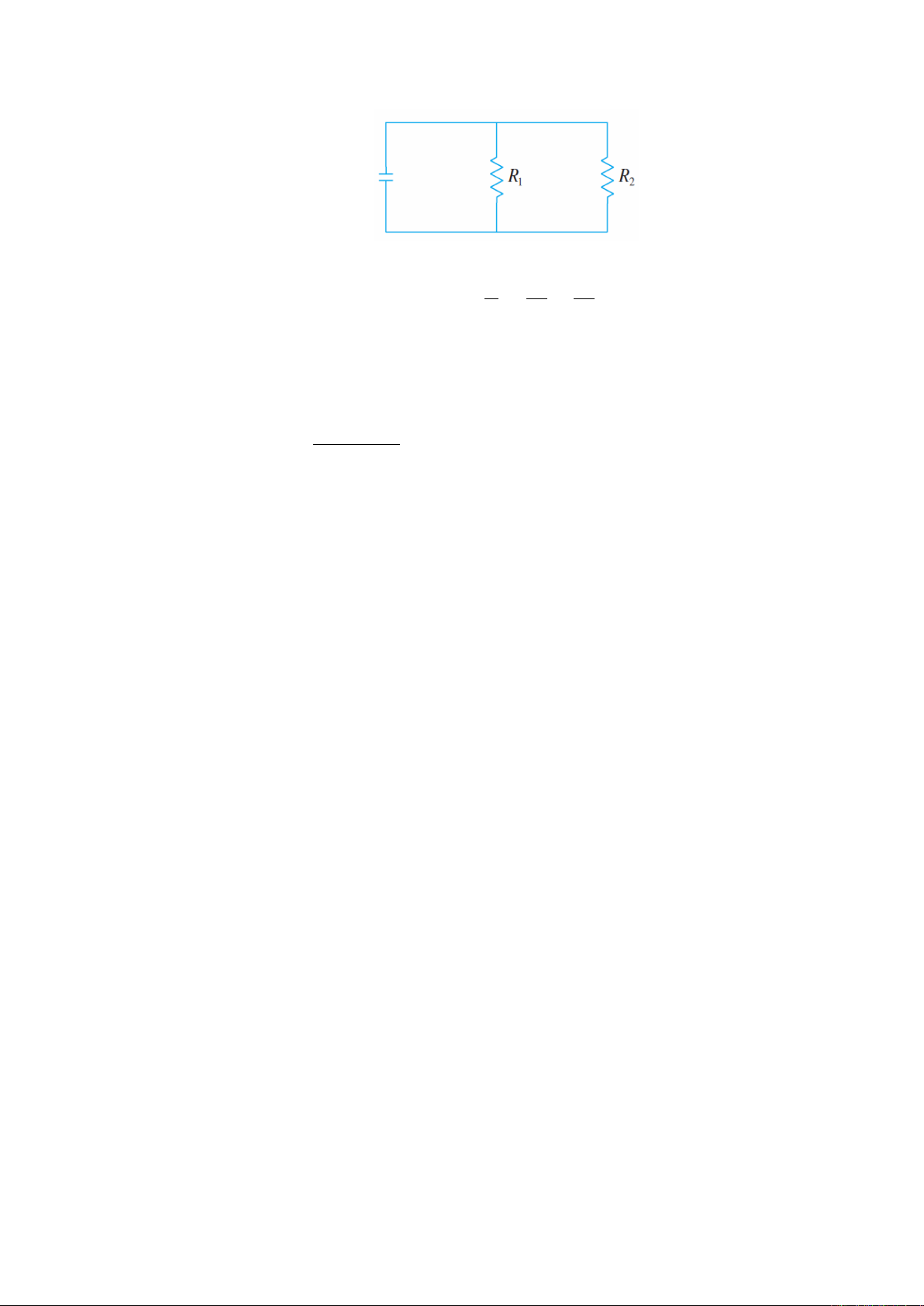
Câu 11. Hai điện trở R1, R2mắc song song như hình vẽ.
Khi đó điện trở tổng thỏa mãn phương trình 1
R=1
R1
+1
R2
.
Nếu khi R1= 80Ω, R2= 100Ω thì R1tăng với tốc độ 0.3Ω/s và R2tăng với tốc độ 0.2Ω/s.
Tính tốc độ thay đổi của R.
A. 0.3122Ω/s B. 0.1213Ω/s C. 0.2257Ω/s D. 0.1321Ω/s
Câu 12. Độ nhạy cảm của mắt đối với ánh sáng được đo bằng tốc độ co dãn đồng tử theo cường độ ánh
sáng. Giả sử R(x) = 40 + 24x0.4
1+4x0.4là diện tích của đồng tử, tính bằng mm2, phụ thuộc vào cường
độ ánh sáng x(tính theo đơn vị cường độ ánh sáng). Tính độ nhạy cảm Scủa mắt khi x= 70.
A. −0.0081 B. −0.0072 C. −0.0121 D. −0.0057
Câu 13. Đường đi của 1 chất điểm được cho bởi phương trình tham số
x= sin 4t, y =−cos 4t
Khẳng định nào sau đây sai?
A. Cả nhận định (1) và (2) đều đúng.
B. (1). Độ lớn của vận tốc chất điểm không đổi.
C. (2). Tiếp tuyến của đường đi luôn vuông góc với đường nối giữa (0,0) và chất điểm.
D. Các nhận định đều sai.
Câu 14. Độ cao của một tên lửa tính bằng feet sau tgiây từ lúc phóng cho bởi hàm số
H(t) = −t3+ 54t2+ 480t+ 6 (t≥0)
Tìm điểm uốn M(t, H(t)) của đồ thị hàm số này và nêu ý nghĩa của M.
A. M(18,20310),tốc độ lớn nhất của tên lửa đạt được sau 18 giây ở độ cao 20310 feet.
B. M(18,20330),tốc độ của tên lửa không đổi sau 18 giây từ độ cao 20330 feet.
C. M(15,20310),sau 15 giây, từ vị trí 20310 feet, độ cao của tên lửa bắt đầu giảm.
D. M(18,20310),20310 feet là độ cao lớn nhất của tên lửa, đạt được sau 18 giây.
Câu 15. Biết tổng chi phí (gồm chi phí cố định và chi phí lưu động) để sản xuất xđơn vị sản phẩm thỏa
mãn hàm số
f(x) = 3200 + 7x($)
với 0≤x≤90. Khẳng định nào dưới đây là đúng?
A. Chi phí tối đa là 3200$.
B. Chi phí để sản xuất 1 đơn vị sản phẩm là 3200$.
C. Chi phí lưu động để sản xuất 1 đơn vị sản phẩm là 7$.
D. Chi phí để lưu động để sản xuất 1 đơn vị sản phẩm là 3207$.
Trang 3/4- Mã đề thi 2000
Câu 16. Khai triển Maclaurin cấp 3 của hàm số f(x) = sin 2x−exlà
A. −x−x2
2+7
3x3+o(x3)B. −1 + x−x2
2−3
2x3+o(x3)
C. −1−x−x2
2−7
6x3+o(x3)D. −1+2x−x2
2+5
2x3+o(x3)
Câu 17. Số nữ cầu thủ bóng đá tại Mỹ tính từ năm từ năm 1985 đến năm 2001 cho bởi hàm số
N(t) = −0.9307t3+ 74.04t2+ 46.8867t+ 3967
ttính theo năm. Khẳng định nào đúng?
A. Trong giai đoạn 1985 đến 2000, tốc độ gia tăng số nữ cầu thủ giảm.
B. Tốc độ gia tăng số nữ cầu thủ lớn nhất vào năm 1996.
C. Trong giai đoạn 1985 đến 2000, tốc độ gia tăng số nữ cầu thủ tăng.
D. Trong giai đoạn 1985 đến 2000, tốc độ gia tăng số nữ cầu thủ không đổi
Câu 18. Cho f(x) = 3x+ 2
5x−3x6=3
5. Khẳng định nào dưới đây là đúng
A. f◦f(x) = −xB. f◦f(x) = −f(x)C. f◦f(x) = −1
xD. f◦f(x) = x
GIẢNG VIÊN RA ĐỀ P. CHỦ NHIỆM BỘ MÔN DUYỆT
ThS. NGUYỄN THỊ XUÂN ANH TS. TRẦN NGỌC DIỄM
Trang 4/4- Mã đề thi 2000
Mã đề thi 2000 ĐÁP ÁN
Câu 1. B.
Câu 2. A.
Câu 3. A.
Câu 4. C.
Câu 5. A.
Câu 6. D.
Câu 7. B.
Câu 8. A.
Câu 9. C.
Câu 10. B.
Câu 11. D.
Câu 12. A.
Câu 13. D.
Câu 14. A.
Câu 15. C.
Câu 16. B.
Câu 17. C.
Câu 18. D.
Trang 1/4- Mã đề thi 2000