
Cải thiện tốc độ tính toán ma trận cơ sở cho
bài toán visual odometry
Nguyễn Hữu Hùng
∗
, Vũ Anh Đức
∗
∗
Viện tích hợp hệ thống
Học Viện Kỹ thuật Quân Sự
Hà Nội, Việt Nam
Email: hungnh.isi.edu.vn
Tóm tắt—Trong các hệ thống dẫn đường tự động ứng
dụng trong robot, xe tự hành, phương pháp dẫn đường sử
dụng hình ảnh thu từ camera đơn hay đôi được sử dụng
rộng rãi nhờ chi phí rẻ và độ chính xác cao. Trong bài báo
này, chúng tôi đề xuất một phương án cải thiện tốc độ tính
toán ma trận cơ sở (essential matrix) bằng cách lựa chọn số
lượng nghiệm thông qua so sánh với vector cơ sở của hai
frame ảnh liền trước. Phương pháp đề xuất được đánh giá
trên tập dữ liệu mở KITTI cho xe tự hành chỉ ra rằng
tốc độ tính toán giảm được 5,6 % so với phương pháp cũ .
Từ khóa—Xử lý ảnh, Dẫn đường bằng hình ảnh, Dẫn
đường robot, Xe tự hành.
I.
GIỚI THIỆU
Phương pháp định vị và xây dựng bản đồ đồng thời
(SLAM)[1] là một kỹ thuật nổi tiếng dành cho các hệ
thống điều hướng tự hành như robot tự hành trên các
hành tinh, robot di chuyển dưới nước và các phương tiện
tự hành bao gồm ô tô tự lái, máy bay không người lái tự
động, đặc biệt là trong các môi trường nguy hiểm cho
tính mạng của con người. VO [2] [3] là một phần thiết
yếu của vSLAM sử dụng hình ảnh, đóng vai trò như
một động cơ lái xe của các hệ thống định vị tự động.
Chuyển động của xe có thể được xác định từ các điểm
đặc trưng trích xuất trong một chuỗi hình ảnh do camera
chụp lại.
Sự chuyển động có thể được tính toán từ một camera
duy nhất. Tuy nhiên, các thuật toán VO sử dụng một
camera thuần túy gặp phải vấn đề về độ lệch tỷ lệ dịch
chuyển ngay cả khi áp dụng điều chỉnh tối ưu toàn cục,
do vấn đề mơ hồ về tỷ lệ dịch chuyển theo chiều sâu.
Thuật toán VO sử dụng hai camera, thường là stereo
camera (SVO) với tham số hiệu chỉnh giữa máy ảnh
trái-phải, quy về đường cơ sở là phương pháp đơn giản
và hiệu quả để giải quyết hiện tượng lệch tỷ lệ đó. Nó
đã được sử dụng từ những năm 1980 với một ứng dụng
thành công trên robot thám hiểm sao Hỏa vào năm 2004
[4]. Hai cách tiếp cận chính đối với VO hình học bao
gồm phương pháp gián tiếp (dựa trên đặc trưng) [1] -
[5] và phương pháp trực tiếp [6] - [7]. Các phương pháp
trực tiếp đặt ra ước tính từ các tương ứng rõ ràng. Các
phương pháp gián tiếp giải quyết việc giảm thiểu năng
lượng của màu sắc hình ảnh và tính năng lỗi cong vênh
để xác định cả tư thế máy ảnh và các thông số bản đồ.
Ví dụ, ORB-SLAM2 [1] là một trong những hệ thống
SLAM đầy đủ sử dụng phương pháp dựa trên tính năng
với phân phối điểm khóa ORB thưa thớt, trong khi DSO
[7] được biết đến như một phương pháp SLAM trực tiếp
đầy đủ. Bên cạnh đó, VISO2 [5] là khung VO phổ biến
mà phép quay và phép tịnh tiến đồng thời thu được bằng
cách thu nhỏ phép chiếu lại được gọi là phương pháp
PnP . Tương tự, Fanfani cũng dụng phương pháp PnP
với lựa chọn khung hình chính và các điểm đặc trưng
[8].
Gần đây, VO [7] dựa trên ma trận cơ sở cho thấy hiệu
suất vượt trội trên tập dữ liệu KITTI so với phương pháp
PnP . Ví dụ, phương pháp SOFT2 đề xuất lược đồ lựa
chọn đối tượng địa lý cẩn thận dựa trên các đặc điểm của
đối tượng địa lý sau khi ước lượng xoay vòng dựa trên
ma trận cơ bản, và sau đó dịch được ước tính bằng cách
giảm thiểu lỗi chiếu lại. Hay phương pháp MESVO_FP
[9] đề xuất tích hợp nhiều khung hình để định vị dựa
trên ma trận thiết yếu bằng cách điều tra sự chuyển đổi
và tích hợp tính năng giữa ba khung hình cuối cùng
trong giao diện người dùng. Ràng buộc vòng kín được
sử dụng để tinh chỉnh tư thế tương đối giữa khung hình
trước đó và khung hình hiện tại từ tư thế của hai khung
hình trước đó. Ngoài ra, vị trí đặc trưng của khung hiện
tại được tinh chỉnh bởi các ràng buộc về hình học từ các
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
124
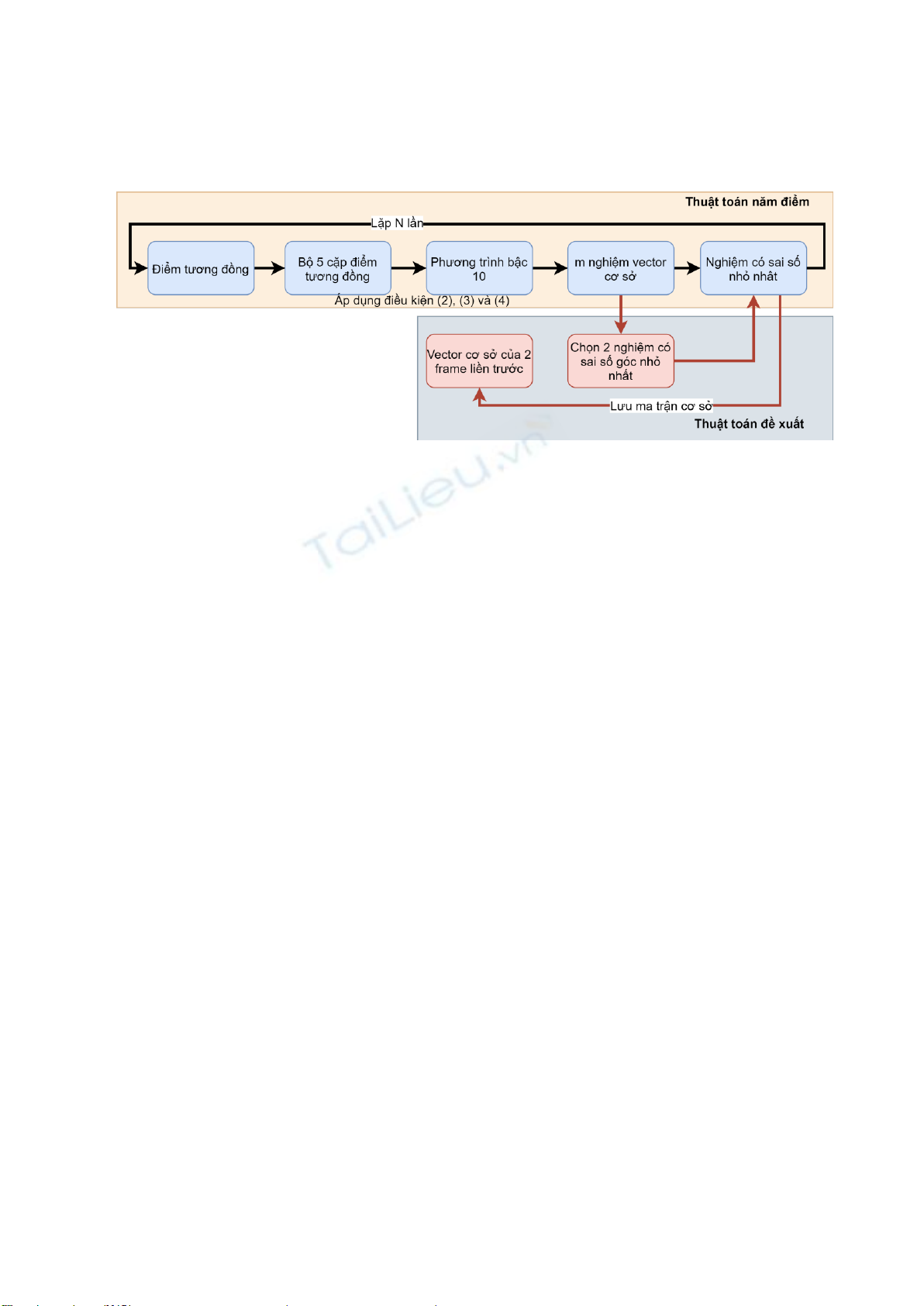
Hình 1. Phương pháp cải thiện tốc độ tính toán. Khổi màu vàng mô tả thuật toán năm điểm [3]. Khôi màu xám mô tả thuật toán đề xuất giảm số
lượng nghiệm đánh giá sai số từ m xuống còn 2 để tăng tốc thời gian tính toán
khung trước đó.
Được biết, xe tự hành thường di chuyển ở tốc độ cao
cho nên sự dịch chuyển không có sự khác biệt đáng kể
về góc quay và hướng nên ma trận cơ sở hay vector cơ
sở gần như ít thay đổi. Từ đó có thể đề xuất phương
pháp để giảm thời gian tính toán. Bài báo này trình bày
một cải tiến tốc độ tính toán ma trận cơ sở cho bài toán
VO bằng cách chọn hai từ m nghiệm bằng các lưu và
so sánh vector cơ sở của hai khung hình liền kề trước
biểu diễn bằng vector 9 × 1. Hai nghiệm này có sai số
góc nhỏ nhất so với vector cơ sở của hai khung hình
liền trước.
Hình 1 mô tả cách tiếp cận được đề xuất dựa trên
thuật toán năm điểm nổi tiếng [3]. Bắt đầu từ 5 cặp
điểm tương đồng được đưa vào các điều kiện (2), (3) ,
(4) để biến đổi thành một phương trình một biến bậc
10. Giải phương trình này chúng ta có tối đa 10 nghiệm
và tìm ra nghiệm có sai số nhỏ nhất dựa trên điều kiện
epipolar. Đóng góp chính của chúng tôi nằm ở chỗ được
đánh dấu là khối màu đỏ, từ N nghiệm thu được chúng
tôi dựa vào vector của 2 frame liền kề trước để chọn
được 2 nghiệm có sai số nhỏ nhất so với vector cơ sở.
Và cuối cùng tìm ra nghiệm có sai số nhỏ nhất từ 2
nghiệm vừa tìm được. Với những cải tiến này, phương
pháp được đề xuất thu được sai số trung bình khi dịch
là 0,87 % và sai số trung bình khi quay là 0,321 độ /
100m có cao hơn một chút so với phương pháp ban đầu
(0,84 % và 0,304) nhưng ở một số frame đã có kết quả
tốt hơn và thời gian thực hiện ngắn hơn so với phương
pháp cũ 5%.
Phần còn lại của bài báo được bố trí như sau. Phần II,
chúng tôi tóm tắt kỹ thuật tính toán ma trận chuyển bao
gồm ma trận quay và vector tịnh tiến dựa trên ma trận
cơ sở và đề xuất của chúng tôi để tăng tốc ma trân cơ sở.
Trong Phần III, chúng tôi đánh giá hiệu suất của phương
pháp được đề xuất trên tập dữ liệu KITTI bằng cách so
sánh nó với các cách tiếp cận thông thường khác.
II.
CẢI THIỆN TỐC ĐỘ TÍNH TOÁN MA TRẬN CƠ SỞ
Phần này tóm tắt ngắn gọn về visual odometry dựa
trên ma trận cơ sở, trong đó các điểm đặc trưng được
trích xuất và xác định các cặp điểm tương đồng trong
[5]. Ước tính ma trận dịch chuyển và dịch chuyển tịnh
tiến là hai phần chính để xác định vị trí của phương
tiện so với vị trí ban đầu. Phương pháp cải tiến thời
gian được mô tả cụ thể tại mục B.
A.
Xác định sự dịch chuyển dựa trên ma trận cơ sở
Sự dịch chuyển của robot được biểu diễn bởi ma trận
quay và vector tịnh tiến. Giá trị của ma trân quay và
hướng của dịch chuyển tịnh tiến có thể được tính toán
thông qua ma trận thiết yếu (E). Ma trận E thể hiện
mối liên hệ của các cặp điểm đặc trưng trích xuất từ
ảnh hiện tại và ảnh liền trước. Nó có thể được thể hiện
qua công thức sau (1)
E
=
T
×
R
(1)
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
125
trong đó, R và T× lần lượt là hai ma trận 3 × 3 bao
gồm cả ma trận quay và ma trận xiên. Hơn nữa, ma trận
cơ bản E phải thỏa mãn hai ràng buộc như sau:
det
(
E
) = 0
,
(2)
và
2
EE
T
E
−
tr
(
EE
T
)
E
=
0
(3)
Mỗi cặp điểm đặc trưng tương đồng 2D (p, q) của hai
khung ảnh thỏa mãn ràng buộc biểu thức
p
T
Eq
=
0
(4)
Kết hợp ràng buộc biểu thức và các phương trình (2) và
(3) này để có được ma trận cơ sở sử dụng thuật toán năm
điểm Nister [3]. Khi ma trận cơ bản được ước lượng thì
ma trận quay R và hướng dịch chuyển t có thể được
khôi phục.
B.
Cải thiện tốc độ tính toán ma trận cơ sở
Như mô tả ở trên, ma trận cơ sở được tính toán từ tập
5 cặp điểm tương đồng. Năm cặp điểm này được đưa
vào các điều kiện ở phương trình (2), (3) và (4). Sau khi
biến đổi các phương trình này thành một phương trình
một biến bậc mười nên tối đa có 10 nghiệm. Theo thuật
toán năm điểm Nister [3], trung bình có 5-6 nghiệm.
Tuy nhiên đối với xe tự hành, chúng thường di chuyển
với tốc độ cao, nên sự dịch chuyển không có nhiều khác
biệt về góc quay và hướng, do đó chúng ta có thể tận
dụng điều kiện này để loại bỏ bớt những nghiệm của ma
trận cơ sở nhằm giảm thời gian tính toán. Ma trân cơ
sở 3 × 3 được biến đổi thành vector cơ sở 9 × 1. Vector
cơ sở của hai frame ảnh liền trước được lưu để loại bỏ
những nghiệm của ma trận cơ sở giữa frame hiện tại và
ngay trước đó Eprv. Phương pháp lựa chọn 2 trong m
nghiệm của ma trận cơ sở với ý tưởng rất đơn giản được
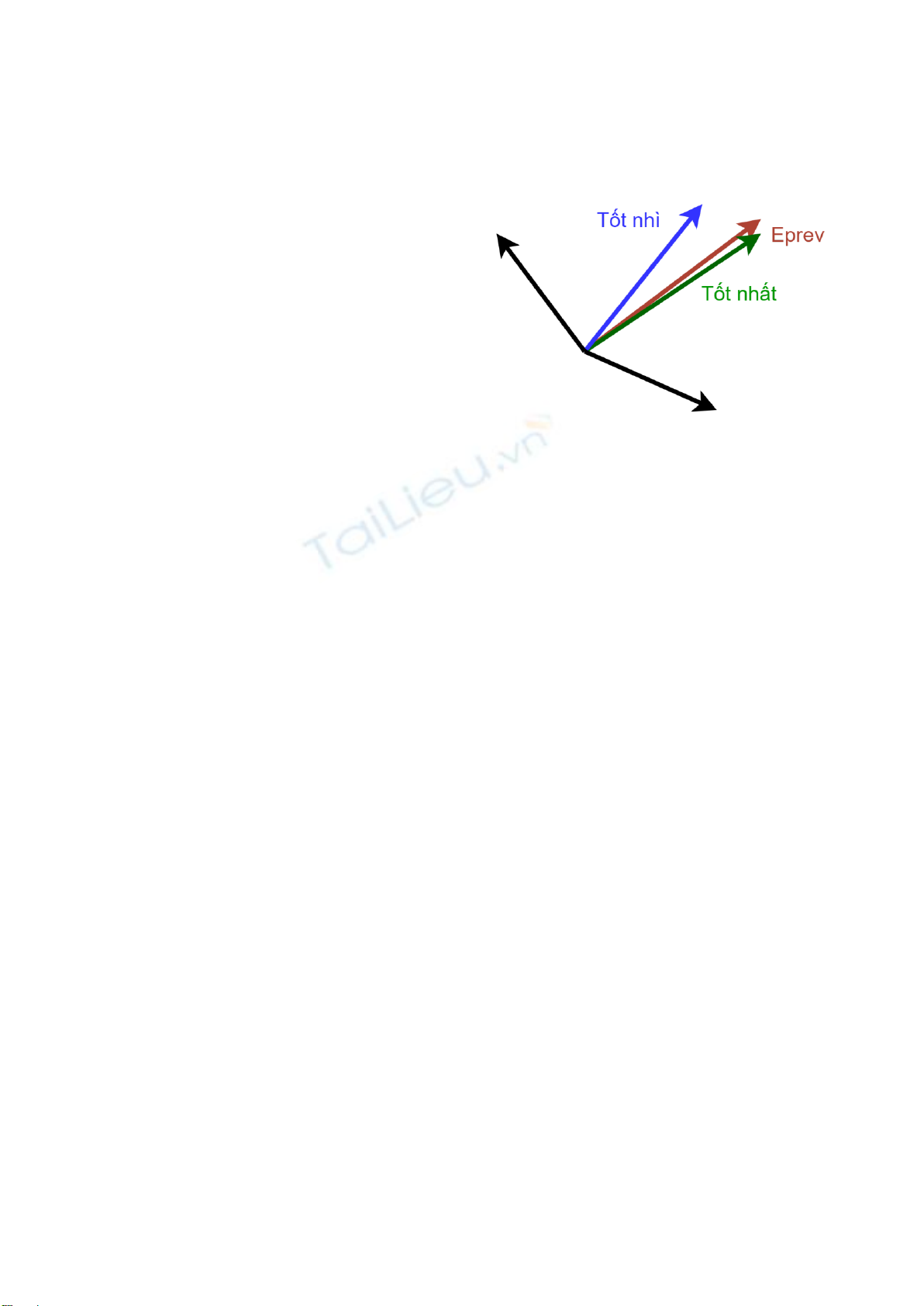
mô tả cụ thể trong Hình 2 Vector cơ sở của 2 khung
hình trước đó Eprev được lưu trữ trước đó. Khi tìm được
m ngiệm của vector cơ sở Ei giữa khung hình hiện tại
và liền kề trước, chúng ta tiến hành đánh giá sai số giữa
sự sai khác góc giữa 2 vector được biểu diễn bằng dot
product.
dot
=
E
prev
E
i
(5)
Chỉ 2 trong m vector (tốt nhất và tốt nhì có sai số góc
nhỏ nhất so với Eprev) được giữ lại cho giai đoạn đánh
giá sai số, m− 2 vector được loại bỏ thường góc quá lớn
so với Eprev. Kết quả của việc đánh giá sai số sẽ chọn
vector có sai số nhỏ nhất cho một bộ cặp 5 điểm. Việc
Hình 2. Phương pháp lựa chọn 2 trong m nghiệm
này thực hiện lặp n lần với N cặp 5 điểm tương đồng
để chọn ra vector cơ sở cuối cùng. Việc tính toán ma
trận quay và dịch chuyển tịnh tiến được thực hiện theo
[3] và vector cơ sở của frame hiện tại và liền trước lại
được lưu vào Eprev đề phục vụ việc so sánh của những
frame tiếp theo.
III.
KẾT QUẢ THỰC NGHIỆM
Chúng tôi đã thử thuật toán của mình trên tập dữ liệu
KITTI để có được đánh giá chi tiết về hiệu suất cả độ
chính xác và thời gian tính toán. Bộ dữ liệu KITTI phổ
biến với các nhà nghiên cứu hệ thống lái xe tự động và
nó bao gồm 22 chuỗi ảnh được chia thành hai phần: 1)
tập dữ liệu đào tạo (00-10) và 2) tập dữ liệu kiểm tra
(11-21). Bộ dữ liệu được thu thập trong các điều kiện
môi trường khác nhau như tốc độ, ánh sáng, điều kiện
bóng tối, các đối tượng chuyển động để đánh giá thuật
toán một cách chính xác. Bộ dữ liệu hỗ trợ một công
cụ cho phép đánh giá hiệu suất của thuật toán một cách
tự động bằng cách đo các sai số tương đối (RMSE) của
quá trình quay và dịch [10]. Nó xác định một số sai số
trung bình của tất cả các chuỗi con có độ dài (100, 200,
..., 800 mét). Để có được đánh giá khách quan, chúng tôi
đã so sánh kết quả thuật toán của mình với các phương
pháp khác nhau như VISO2 [5] và MESVO_PF [9]. Kết
quả của phương pháp đề xuất là dựa trên phương pháp
MESVO_PF [9] chỉ với sự thay đổi về cách thức lựa
chọn số lượng nghiệm.
Thuật toán của chúng tôi được so sánh với các phương
pháp khác như VISO2[5], MESVO_PF [9] để đánh giá
hiệu suất của nó. Sai số RE là sai số ma trận quay trung
bình (độ / 100m) và sai số dịch chuyển tịnh tiến TE (%)
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
126
Bảng I
ĐÁNH GIÁ ĐỘ CHÍNH XÁC TRÊN BỘ DỮ LIỆU KITTI
Sec
Num
VISO2 [5]
MESVO_PF [9]
Đề xuất
T
E
(%)
RE
( deg )
100m
T
E
(%)
RE
( deg )
100m
T
E
(%)
RE
( deg )
100m
Avg
2,43
1,106
0,84
0,304
0,87
0,321
0
2,46
1,181
0,78
0,350
0,82
0,355
1
4,42
1,015
1,62
0,269
0,68
0,344
2
2,19
0,808
0,83
0,264
0,75
0,269
3
2,54
1,198
0,77
0,247
0,92
0,315
4
1,02
0,866
0,75
0,229
0,55
0,195
5
2,07
1,124
0,63
0,264
0,67
0,304
6
1,31
0,917
0,83
0,310
0,97
0,338
7
2,30
1,771
1,20
0,877
0,88
0,527
8
2,74
1,336
1,03
0,310
1,17
0,361
9
2,76
1,152
0,78
0,201
0,93
0,252
10
1,63
1,118
0,82
0,292
0,78
0,327
được tóm tắt trong Bảng II. Nó cho thấy RMSE của tất
cả 11 chuỗi cũng như chi tiết trung bình của chúng cho
ba cách tiếp cận. Phương pháp của chúng tôi được đánh
giá với hai tùy chọn: 1) tích hợp nhiều khung với chỉ tinh
chỉnh tư thế (MESVO_P) và 2) tích hợp nhiều khung với
cả tinh chỉnh tư thế và tính năng (MESVO_PF)
1000
800
600
400
500
200
400
0
300
200
-200
-100 0 100 200 300 400
X(m)
500 600 700
100 Hình 4. Quỹ đạo của Chuỗi 02 cho 3 cách tiếp cận so với ground-truth
0
-100
-300 -200
-100 0 100 200 300
X(m)
MESVO_FP và phương pháp mới lần lượt là 0,87 độ /
100m, 0,23 độ / 100m và 0,2 độ / 100m. Mặc dù sử dụng
cùng một phương pháp dựa trên ma trận thiết yếu tương
tự như VISO2 và MESVO_FP, phương pháp của chúng
Hình 3. Quỹ đạo của Chuỗi 00 cho 3 cách tiếp cận so với ground-truth
Đối với các lỗi dịch và xoay, thuật toán của chúng tôi
nhận được kết quả trung bình thấp hơn so với VISO2
và cao hơn một chút so với MESVO_FP nhưng có kết
quả trong một số chuỗi tốt hơn MESVO_FP. Ví dụ, sai
số quay trung bình của VISO2, MESVO_FP và phương
pháp mới lần lượt là 1,106 độ / 100m, 0,304 độ / 100m
và 0,321 độ / 100m, sai số quay ở chuỗi 4 của VISO2,
tôi với việc dựa trên vector của 2 frame liền để chọn 2
nghiệm làm giảm sai số xoay trung bình khoảng 30%
so với VISO2 và nhỉnh hơn 5,5% so với MESVO_FP.
Độ chính xác của ma trận cơ bản dựa trên xoay đã
được chứng minh là cao hơn so với VISO2 và cao hơn
ở một số chuỗi so với MESVO_FP. Sai số dịch thuật
của VISO2 và MESVO_FP tương ứng là 2,43%, 0,84%,
trong khi các phương pháp tiếp cận đề xuất của chúng tôi
là 0,87%. Có nghĩa là các lỗi dịch thuật trung bình của
GT
VISO2
MESVO_PF
Ours
GT
VISO2
MESVO_PF
Ours
Z(m)
Z(m)
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
127

Bảng II
ĐÁNH GIÁ THỜI GIAN VÀ SỐ LƯỢNG NGHIỆM
các phương pháp tiếp cận của chúng tôi giảm khoảng
36% so với VISO2 và thấp hơn 3,6% so với MESVO_FP
kể từ khi áp dụng phương pháp chọn nghiệm dựa trên
2 frame liền kề trước. Dù sai số có tăng lên 1 chút ít
tuy nhiên những chuỗi có sai số lớn như chuỗi 01 và
07, phương pháp của chúng tôi có xu thế giảm do việc
duy trì được điều kiện tính toán ma trận cơ sở, trong
khi đó các phương pháp khác việc tính toán dễ bị sai
do số lượng inlier ít .
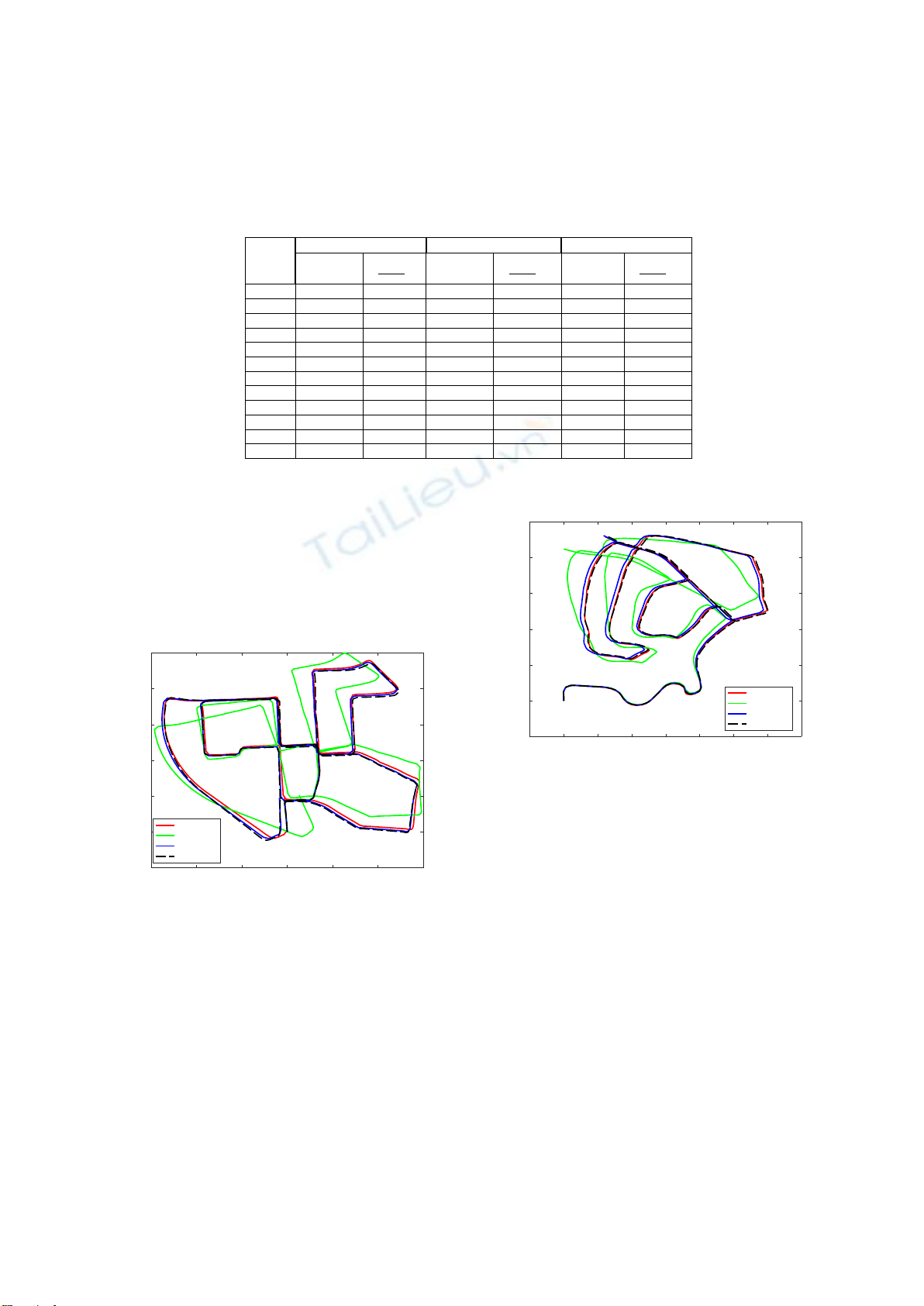
Để minh chứng cho độ chính xác, chúng tôi vẽ lại
đường đi của xe tự hành với Chuỗi 00 và Sector Chuỗi
trong bộ dữ liệu KITTI. Đường đỏ là đường ground-truth
xây dựng từ Gps và Imu được coi là đường đi chính xác
của phương tiện. Đường màu xanh lá cây và màu xanh
da trời lần lượt là kết quả của phương pháp VISO2 và
MES_FP. Đường màu đen là kết quả của phương pháp
đề xuất. Kết quả của phương pháp tương đương so với
MES_FP do nó được xây dựng từ phương pháp này.
Chúng tôi đánh giá thời gian tính toán của ma trận
cơ sở của 2 phương pháp : (1) phương pháp 5 điểm
được dùng trong MESVO_FP và (2) phương pháp chọn
hai vector nghiệm đề xuất. Ngoài ra chúng tôi cũng đo
số lượng nghiệm trung bình của 2 phương pháp. Cả 2
kết quả được tổng hợp trong Bảng II. Thời gian tính
toán của phương pháp đề xuất trung bình là 55,3ms so
với phương pháp năm điểm sử dụng trong MESVO_FP
58,5ms giảm 5,6%. Trong đó số lượng nghiệm giảm từ
4,2 xuống còn 2.
chính xác cải thiện tốt ở nhưng chuỗi ảnh mà xe đi tốc
độ cao, số lượng điểm đặc trung thu được ít. Trong tương
lai, chúng tôi sẽ tiếp tục nghiên cứu các hướng chuyên
sâu khác để có thể cải thiện hiệu suất hơn nữa cho bài
toán visual odometry cho xe tự hành và máy bay tự lái.
TÀI LIỆU
[1]
Hans P Moravec. The stanford cart and the cmu rover. Proceed-
ings of the IEEE, 71(7):872–884, 1983.
[2]
Huu Hung Nguyen, Quang Thi Nguyen, Cong Manh Tran, and
Dong-Seong Kim. Adaptive essential matrix based stereo visual
odometry with joint forward-backward translation estimation. In
International Conference on Industrial Networks and Intelligent
Systems, pages 127–137. Springer, 2020.
[3]
David Nistér, Oleg Naroditsky, and James Bergen. Visual
odometry. In Proceedings of the 2004 IEEE Computer Society
Conference on Computer Vision and Pattern Recognition, 2004.
CVPR 2004., volume 1, pages I–I. Ieee, 2004.
[4]
Raul Mur-Artal and Juan D Tardós. Orb-slam2: An open-source
slam system for monocular, stereo, and rgb-d cameras. IEEE
transactions on robotics, 33(5):1255–1262, 2017.
[5]
Bernd Kitt, Andreas Geiger, and Henning Lategahn. Visual
odometry based on stereo image sequences with ransac-based
outlier rejection scheme. In 2010 ieee intelligent vehicles
symposium, pages 486–492. IEEE, 2010.
[6]
Huu Hung Nguyen and Sukhan Lee. Orthogonality index based
optimal feature selection for visual odometry. IEEE Access,
7:62284–62299, 2019.
[7]
Igor Cvisˇic´ and Ivan Petrovic´. Stereo odometry based on careful
feature selection and tracking. In 2015 European Conference on
Mobile Robots (ECMR), pages 1–6. IEEE, 2015.
[8]
Marco Fanfani, Fabio Bellavia, and Carlo Colombo. Accurate
keyframe selection and keypoint tracking for robust visual odom-
etry. Machine Vision and Applications, 27(6):833–844, 2016.
[9]
Huu-Hung Nguyen, The-Tien Nguyen, Xuan-Phuc Nguyen,
Cong-Manh Tran, and Quang-Thi Nguyen. Multiple frame
integration for essential matrix-based visual odometry. In 2022
16th International Conference on Ubiquitous Information Man-
agement and Communication (IMCOM), pages 1–6. IEEE, 2022.
[10]
Andreas Geiger, Philip Lenz, and Raquel Urtasun. Are we ready
for autonomous driving? the kitti vision benchmark suite. In
2012 IEEE conference on computer vision and pattern recogni-
tion, pages 3354–3361. IEEE, 2012.
IV.
KẾT LUẬN
Trong bài báo này chúng tôi đã nghiên cứu cải tiến
tốc độ tính toán ma trận cho bài tóan visual odometry
bằng phương pháp chọn 2 nghiệm từ m nghiệm dựa trên
vector của 2 frame liền kề để cuối cùng chọn ra được
nghiệm có sai số nhỏ nhất. Chúng tôi chứng minh được
rằng khi sử dụng phương pháp trên thì sai số tương đối
đã được cải thiện nhiều so với phương pháp VISO2.
Tuy sai số tương đối có phần kém hơn phương pháp
MESVO_PF nhưng thời gian thực hiện thuật toán nhanh
hơn phương pháp trên khoảng 5,6%. Bên cạnh đó độ
MESVO_PF
Đề xuất
Số lượng nghiệm
4,2
2
Thời gian trung bình(ms)
58,6
55,3
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
128

















![Bài tập Đại số tuyến tính [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250930/dkieu2177@gmail.com/135x160/79831759288818.jpg)








