intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Cẩm nang cho mùa thi: Tuyển chọn 50 bài toán điển hình Min, Max - Nguyễn Hữu Biển

Chia sẻ: Phan Hùng | Ngày: | Loại File: PDF | Số trang:28

Thêm vào BST
Báo xấu
183
lượt xem 35
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Cẩm nang cho mùa thi "Tuyển chọn 50 bài toán điển hình Min, Max" giới thiệu đến các bạn hệ thống 50 bài toán tìm giá trị lớn nhất nhỏ nhất có hướng dẫn lời giải, mời các bạn cùng tham khảo để củng cố lại kiến thức và làm quen với dạng bài tập Min, Max.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Cẩm nang cho mùa thi: Tuyển chọn 50 bài toán điển hình Min, Max - Nguyễn Hữu Biển

  1. CẨM NANG CHO MÙA THI TUYỂN CHỌN 50 BÀI TOÁN ĐIỂN HÌNH MIN - MAX (ÔN THI THPT QUỐC GIA) NGUYỄN HỮU BIỂN https://www.facebook.com/ng.huubien Email: ng.huubien@gmail.com
  2. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Bài 1: Cho ba số dương x, y, z thỏa mãn: x + y + z = 1 x+ y y+z z+x Tìm giá trị nhỏ nhất của: P = + + xy + z yz + x zx + y Hướng dẫn Ta có x + y + z = 1 ⇒ x + y = 1 − z , ta có: x+ y 1− z 1− z = = xy + z xy + 1 − x − y (1 − x )(1 − y ) y+z 1− x 1− x = = yz + x yz + 1 − y − z (1 − y )(1 − z ) z+x 1− y 1− y = = zx + y zx + 1 − x − z (1 − x )(1 − z ) x+ y y+z z+x 1− z 1− x 1− y Khi đó P = + + = + + xy + z yz + x zx + y (1 − x)(1 − y ) (1 − y )(1 − z ) (1 − x )(1 − z ) 1− z 1− x 1− y ≥ 33 . . =3. (1 − x)(1 − y ) (1 − y )(1 − z ) (1 − x)(1 − z ) 1 Vậy MinP = 3 đạt được khi x = y = z = 3 Bài 2: Cho x, y, z là ba số thực tùy ý thỏa mãn x + y + z = 3. 1 1 1 x y z Chứng minh rằng với ∀a ≥ 1 ta luôn có : x + y+ z ≥ x+ y+ z. a a a a a a Hướng dẫn * Với a = 1 ta thấy BĐT đúng . * Ta xét khi a > 1. t 1 1 Hàm số y = y = t =   nghịch biến với ∀t ∈ R , khi a > 1. a a Khi đó ta có 1 1 x y x y Ta có : ( x − y )( x − y ) ≤ 0, ∀x, y ∈ R. Suy ra x + y ≤ y + x (1) a a a a a a y z z y z x x z Chứng minh tương tự y + z ≤ y + z (2) z + x ≤ z + x (3) a a a a a a a a x y z y+ z z+ x x+ y Cộng vế với vế (1) ,(2) và (3) ta được 2( x + y + z ) ≤ x + y + z (4) a a a a a a x y z Cộng 2 vế của (4) với biểu thức x + y + z ta được a a a x y z x+ y+ z x+ y+ z x+ y+ z 1 1 1 3( x + y + z)≤ x + y + z = ( x + y + z )( x + y + z ) a a a a a a a a a NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 1
  3. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 1 1 1 x y z Suy ra x + y + z ≥ x + y + z . ( do x + y + z = 3 ) a a a a a a Dấu bằng xảy ra khi chỉ khi x = y = z = 1. (đpcm) Bài 3: Cho a, b, c là ba số thực dương thỏa mãn điều kiện ab + bc + ca = 3. 1 1 1 1 Chứng minh rằng: 2 + 2 + 2 ≤ . 1 + a (b + c) 1 + b (c + a ) 1 + c (a + b) abc Hướng dẫn Áp dụng BĐT Cauchy cho 3 số dương ta có: 3 = ab + bc + ca ≥ 3 3 (abc)2 ⇒ abc ≤ 1 . 1 1 Suy ra: 1 + a 2 (b + c) ≥ abc + a 2 (b + c) = a(ab + bc + ca) = 3a ⇒ 2 ≤ (1). 1 + a (b + c) 3a 1 1 1 1 Tương tự ta có: 2 ≤ (2), 2 ≤ (3). 1 + b (c + a ) 3b 1 + c (a + b) 3c Cộng (1), (2) và (3) theo vế với vế ta có: 1 1 1 1 1 1 1 ab + bc + ca 1 2 + 2 + 2 ≤ ( + + )= = □. 1 + a (b + c) 1 + b (c + a ) 1 + c (a + b) 3 c b c 3abc abc Dấu “=” xảy ra khi và chỉ khi abc = 1, ab + bc + ca = 3 ⇒ a = b = c = 1, (a, b, c > 0). Bài 4: Cho x, y, z là các số thực thỏa mãn − 1 − 2 2 < x < −1 + 2 2 , y > 0, z > 0 và x + y + z = −1 . 1 1 1 Tìm giá trị nhỏ nhất của biểu thức P = 2 + + . ( x + y) ( x + z) 8 − ( y + z)2 2 Hướng dẫn 1 1 1 1 1 1 Ta có P = 2 + 2 + 2 = 2 + 2 + (−1 − z ) (−1 − y ) 8 − (−1 − x) (1 + y ) (1 + z ) 8 − (1 + x) 2 1 1 1 Ta sẽ chứng minh 2 + 2 ≥ (1 + y ) (1 + z ) 1 + yz 1 1 1 Thật vậy: 2 + 2 ≥ ⇔ (1 + yz)[(1 + z ) 2 + (1 + y ) 2 ] ≥ [(1 + z )(1 + y )]2 . (1 + y ) (1 + z ) 1 + yz ⇔ (1 + yz )( 2 + 2 z + 2 y + z 2 + y 2 ) ≥ (1 + zy + z + y ) 2 ⇔ 2( z + y )(1 + zy ) + 2(1 + yz ) + (1 + zy )( y − z ) 2 + 2 zy (1 + yz ) ≥ (1 + zy ) 2 + 2( z + y )(1 + zy ) + ( z + y ) 2 ⇔ (1 + zy )( y − z ) 2 + 2 + 4 yz + 2 y 2 z 2 − (1 + yz ) 2 − ( y − z ) 2 − 4 yz ≥ 0 ⇔ yz ( y − z ) 2 + (1 − yz ) 2 ≥ 0 (hiển nhiên đúng). Dấu “=” xảy ra khi y = z = 1 . 2 2 2 y+z  y+z ( −1 − x ) (1 + x) Ta lại có ≥ yz ⇒ yz ≤   = = 2  2  4 4 NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 2
  4. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 1 1 1 1 4 Do đó 2 + 2 ≥ ≥ 2 = (1 + y ) (1 + z ) 1 + yz (1 + x) 4 + (1 + x) 2 1+ 4 4 1 ⇒P≥ + 4 + (1 + x) 8 − ( x + 1) 2 2 Do − 1 − 2 2 < x < −1 + 2 2 nên ( x + 1) 2 ∈ [0;8) . 4 1 Đặt t = (1 + x) 2 ⇒ t ∈ [0;8) và P ≥ + 4+t 8−t 4 1 4 1 − 3t 2 + 72t − 240 Xét f (t ) = + với t ∈ [0;8) . 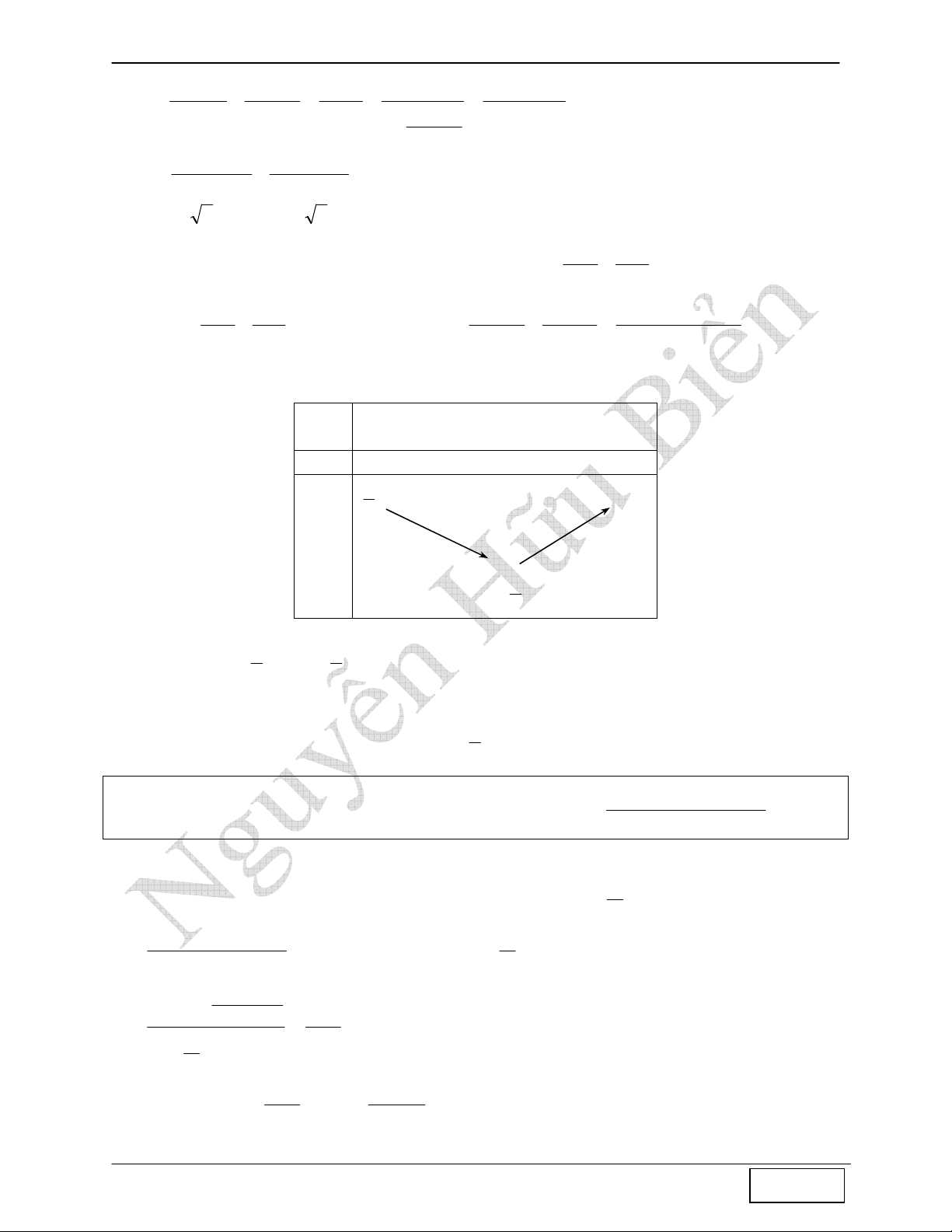f ' (t ) = − + = 4+t 8−t (4 + t ) 2 (8 − t ) 2 (4 + t ) 2 (8 − t ) 2 f ' (t ) = 0 ⇔ −3t 2 + 72t − 240 = 0 ⇔ t = 4; t = 20 (loại) Bảng biến thiên 0 4 t 8 f’(t) - 0 + 9 8 +∞ f(t) 3 4 (1 + x) 2 = 4 3 3   x = −3 Do đó P ≥ f (t ) ≥ và P = khi  y = z = 1 ⇔ 4 4  x + y + z = −1  y = z = 1  3 Vậy min P = khi x = −3, y = z = 1 4 Bài 5: Cho x,y ∈ R và x, y > 1. Tìm giá trị nhỏ nhất của P = (x 3 + y3 ) − ( x2 + y 2 ) ( x − 1)( y − 1) Hướng dẫn t2 Đặt t = x + y ; t > 2. Áp dụng BĐT 4xy ≤ (x + y)2 ta có xy ≤ 4 t 3 − t 2 − xy (3t − 2) t2 P= . Do 3t - 2 > 0 và − xy ≥ − nên ta có xy − t + 1 4 t 2 (3t − 2) t3 − t 2 − 4 t2 P≥ = t2 t−2 − t +1 4 t2 t 2 − 4t Xét hàm số f (t ) = ; f '(t ) = ; f’(t) = 0 ⇔ t = 0 v t = 4. t−2 (t − 2) 2 NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 3
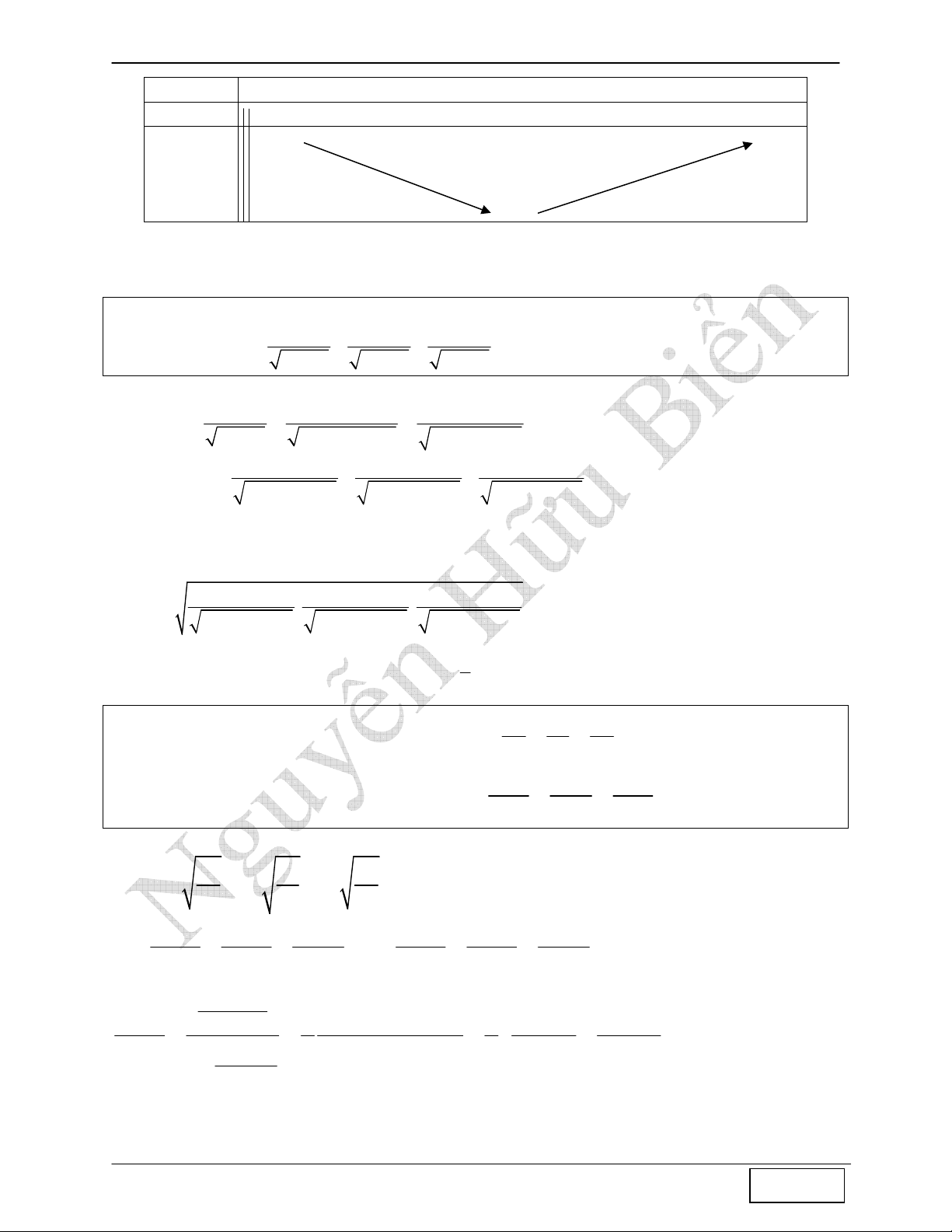
  5. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 t 2 4 +∞ f’(t) - 0 + +∞ +∞ f(t) 8 x + y = 4 x = 2 Do đó min P = min f (t ) = f(4) = 8 đạt được khi  ⇔ (2;+∞ )  xy = 4 y = 2 Bài 6 : Cho a,b,c là các số dương thỏa mãn a + b + c = 1. a +b b +c c +a Chứng minh rằng: + + ≥3 ab + c bc + a ca + b Hướng dẫn a +b 1−c 1−c * Biến đổi = = ab + c ab + 1 − b − a (1 − a )(1 − b ) 1−c 1−b 1−a * Từ đó VT = + + (1 − a )(1 − b ) (1 − c )(1 − a ) (1 − c )(1 − b ) Do a,b,c dương và a+b+c=1 nên a,b,c thuộc khoảng (0;1) => 1-a,1-b,1-c dương * Áp dụng bất đẳng thức Côsi cho ba số dương ta được 1−c 1−b 1−a VT ≥ 3. 3 . . =3 (đpcm) (1 − a )(1 − b ) (1 − c )(1 − a ) (1 − c )(1 − b ) 1 Đẳng thức xảy ra khi và chỉ khi a = b = c = 3 yz zx xy Bài 7: Cho các số thực dương x, y, z thỏa mãn: + + = 1. x y z 1 1 1 Tìm giá trị lớn nhất của biểu thức: A = + + . 1− x 1− y 1− z Hướng dẫn yz zx xy Đặt a = ,b = ,c = . Ta có a, b, c > 0 và a 2 + b 2 + c 2 = 1 . Ta có: x y z 1 1 1 bc ca ab A= + + = 3+ + + . Dễ có: 1 − bc 1 − ca 1 − ab 1 − bc 1 − ca 1 − ab ( b + c )2 2 bc 4 1 ( b + c ) 1  b2 c2  ≤ = ≤  +  1 − bc b2 + c 2 2 b2 + a 2 + c 2 + a 2 2  b2 + a 2 c 2 + a 2  1− 2 NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 4
  6. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 ca 1  c2 a2  ab 1  a2 b2  Tương tự có: ≤  +  và ≤  +  1 − ca 2  c 2 + b 2 a 2 + b 2  1 − ab 2  a 2 + c 2 b 2 + c 2  3 9 từ đó: A ≤ 3 + = . Dấu bằng xảy ra khi x = y = z =1/3 2 2 Bài 8: Cho a, b, c là các số thực dương và a + b + c = 3 . 2 abc Tìm giá trị lớn nhất của biểu thức P = +3 3 + ab + bc + ca (1 + a )(1 + b )(1 + c ) Hướng dẫn Áp dụng Bất đẳng thức: ( x + y + z ) 2 ≥ 3( xy + yz + zx) , ∀x, y , z ∈ ℜ ta có: (ab + bc + ca )2 ≥ 3abc(a + b + c) = 9abc > 0 ⇒ ab + bc + ca ≥ 3 abc Ta có: (1 + a )(1 + b)(1 + c ) ≥ (1 + 3 abc )3 , ∀a, b, c > 0 . Thật vậy: (1+ a)(1+ b)(1+ c) = 1+ (a + b + c) + (ab + bc + ca) + abc ≥1+ 33 abc + 33 (abc)2 + abc = (1+ 3 abc)3 3 2 abc Khi đó: P ≤ + = Q (1). 3(1 + abc ) 1 + 3 abc 3 Đặt abc = t ; vì a, b, c > 0 nên 0 < abc ≤  6 a+b+c  =1  3  2 t2 2t ( t − 1) ( t 5 − 1) Xét hàm số Q = + , t ∈ ( 0;1] ⇒ Q′(t ) = ≥ 0, ∀t ∈ ( 0;1] . 3(1 + t 3 ) 1 + t 2 3 2 2 2 ( )( ) 1 + t 1 + t 1 1 Do đó hàm số đồng biến trên ( 0;1] ⇒ Q = Q ( t ) ≤ Q (1) = (2). Từ (1) và (2): P ≤ . 6 6 1 Vậy maxP = , đạt được khi và và chi khi : a = b = c = 1 . 6 Bài 9: Cho a, b, c là các số dương và a + b + c = 3 . bc ca ab Tìm giá trị lớn nhất của biểu thức: P = + + 3a + bc 3b + ca 3c + ab Hướng dẫn bc bc bc bc  1 1  Vì a + b + c = 3 ta có = = ≤  +  3a + bc a (a + b + c) + bc (a + b)(a + c) 2  a+b a+c  1 1 2 Vì theo BĐT Cô-Si: + ≥ , dấu đẳng thức xảy ra ⇔ b = c a+b a+c (a + b)(a + c) ca ca  1 1  ab ab  1 1  Tương tự ≤  +  và ≤  +  3b + ca 2 b+a b+c 3c + ab 2  c+a c+b  bc + ca ab + bc ab + ca a + b + c 3 Suy ra P ≤ + + = = , 2(a + b) 2(c + a ) 2(b + c) 2 2 3 Đẳng thức xảy ra khi và chỉ khi a = b = c = 1. Vậy max P = khi a = b = c = 1. 2 NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 5
  7. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Bài 10: Cho a, b, c là các số dương và a + b + c = 3 . Tìm giá trị lớn nhất của biểu thức bc ca ab P= + + . 3a + bc 3b + ca 3c + ab Hướng dẫn bc bc bc bc  1 1  Vì a + b + c = 3 ta có = = ≤  +  3a + bc a (a + b + c) + bc (a + b)(a + c) 2  a+b a+c  1 1 2 Vì theo BĐT Cô-Si: + ≥ , dấu đẳng thức xảy ra ⇔ b = c a+b a+c (a + b)(a + c) ca ca  1 1  ab ab  1 1  Tương tự ≤  +  và ≤  +  3b + ca 2 b+a b+c 3c + ab 2  c+a c+b  bc + ca ab + bc ab + ca a + b + c 3 Suy ra P ≤ + + = = , 2(a + b) 2(c + a) 2(b + c) 2 2 3 Đẳng thức xảy ra khi và chỉ khi a = b = c = 1. Vậy max P = khi a = b = c = 1. 2 Bài 11: Cho ba số thực không âm a, b, c thỏa mãn: a2009 + b2009 + c2009 = 3. Tìm giá trị lớn nhất của biểu thức: P = a4 + b4 + c4. Hướng dẫn Áp dụng bất đẳng thức Cô-si cho 2005 số 1 và 4 số a2009 ta có: 1 + 1  + 1 + a 2009 + a 2009 + a 2009 + a 2009 ≥ 2009.2009 a 2009 .a 2009 .a 2009 .a 2009 = 2009.a 4 (1) + ...  2005 Tương tự: 1 + 1  + 1 + b 2009 + b 2009 + b 2009 + b 2009 ≥ 2009.2009 b 2009 .b 2009 .b 2009 .b 2009 = 2009.b 4 (2) + ...  2005 1 + 1  + 1 + c 2009 + c 2009 + c 2009 + c 2009 ≥ 2009.2009 c 2009 .c 2009 .c 2009 .c 2009 = 2009.c 4 (3) + ...  2005 Từ (1), (2), (3) ta được: 6015 + 4(a 2009 + b2009 + c 2009 ) ≥ 2009(a 4 + b 4 + c 4 ) ⇔ 6027 ≥ 2009(a 4 + b4 + c 4 ) . Từ đó suy ra P = a 4 + b4 + c 4 ≤ 3 Mặt khác tại a = b = c = 1 thì P = 3 nên giá trị lớn nhất của P = 3. Bài 12: Cho x, y, z ≥ 0 thoả mãn x + y + z > 0. x3 + y 3 + 16 z 3 Tìm giá trị nhỏ nhất của biểu thức P = 3 (x + y + z) Hướng dẫn 3 Trước hết ta có: x + y 3 3 ≥ ( x + y ) (biến đổi tương đương) 2 ⇔ ... ⇔ ( x − y ) ( x + y ) ≥ 0 4 3 3 ( x + y ) + 64 z 3 ( a − z ) + 64 z 3 3 Đặt x + y + z = a. Khi đó 4 P ≥ 3 = 3 = (1 − t ) + 64t 3 a a z (với t = , 0 ≤ t ≤1) a NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 6
  8. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Xét hàm số f(t) = (1 – t)3 + 64t3 với t ∈ [ 0;1] . Có 1 f '(t ) = 3 64t 2 − (1 − t )  , f '(t ) = 0 ⇔ t = ∈ [ 0;1] 2   9 Lập bảng biến thiên 64 16 ⇒ Minf ( t ) = ⇒ GTNN của P là đạt được khi x = y = 4z > 0 t∈[ 0;1] 81 81 Bài 13: Cho ba số dương x,y,z thỏa x + y + z = 4 và xyz = 2. Tìm GTNN của biểu thức: P = x4 + y4 + z4 Hướng dẫn 2 i P = ( x 2 + y 2 + z 2 ) − 2( x 2 y 2 + y 2 z 2 + z 2 x 2 ) 2 = ( x + y + z ) − 2 ( xy + yz + zx )  − 2 ( xy + yz + zx ) − 2 xyz ( x + y + z )  2 2     2 = 16 − 2 ( xy + yz + zx )  − 2 ( xy + yz + zx ) − 16  i Đặt t = xy + yz + zx = x(y + z) + yz 2 2 2 + Từ gt ⇒ y + z = 4 − x, yz = ⇒ t = x ( 4 − x ) + = − x 2 + 4 x + x x x 2 8 + Ta có: ( y + z ) 2 ≥ 4 yz ⇒ ( 4 − x ) ≥ ⇔ x 3 − 8 x 2 + 16 x − 8 ≥ 0 x 2 ( ⇔ ( x − 2 ) x − 6 x + 4 ≥ 0 (*) ) Giải BĐT (*) giao với điều kiện 0 < x < 4 ta đươc: 3 − 5 ≤ x ≤ 2 5 5 −1 + Khảo sát hàm số t theo biến x với 3 − 5 ≤ x ≤ 2 ta tìm được: 5 ≤ t ≤ 2 2 i P = (16 − 2t ) − 2(t 2 − 16) = 2t 2 − 64t + 288 5 5 −1 Khảo sát hàm số : f(t) = 2t2 – 64t + 288 với 5 ≤ t ≤ ta được: 2 5 5 −1 M inf(t ) = 383 − 165 5 khi t = , Maxf (t ) = 18 khi t = 5 2 1+ 5 Suy ra: Pmin = 383 − 165 5 đạt được chẳng hạn x = 3 − 5, y = z = 2 Pmax = 18 đạt được chẳng hạn khi x = 2, y = z = 1 Bài 14: Cho các số thực x; y thay đổi. Tìm giá trị nhỏ nhất của biểu thức: P = x 2 + y 2 + 2 x + 1 + x 2 + y 2 − 2 x + 1 + y − 2 . Hướng dẫn P = x2 + y 2 + 2 x + 1 + x2 + y2 − 2x + 1 + y − 2 Xét các điểm M(x−1; −y) , N(x+1; y). Ta có OM + ON ≥ MN ⇔ ( x − 1)2 + y 2 + ( x + 1)2 + y 2 ≥ 4 + 4 y 2 ⇒ P ≥ 2 1 + y 2 + y − 2 = f ( y) NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 7
  9. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 2y TH1: y ≤ 2: f ( y ) = 2 1 + y 2 + 2 − y ⇒ f '( y ) = −1 1 + y2 y ≥ 0 3 f '( y ) = 0 ⇔ 2 y = 1 + y 2 ⇔  2 ⇔y= 3 y = 1 3  3 Lập bảng biến thiên f(y) ⇒ min f ( y ) = f   = 2+ 3 x∈( −∞.2]  3  TH2: y ≥ 2: f ( y ) = 2 1 + y 2 + y − 2 ≥ 2 5 > 2 + 3 Vậy P ≥ 2 + 3 ∀x; y . 3 Do đó MinP = 2 + 3 khi x = 0 ; y = 3 Bài 15: Cho các số thực dương a,b,c thỏa a + b + c =3. Tính góc giá trị nhỏ nhất của biểu a 2 + bc b 2 + ca c 2 + ab thức P = + + b + ca c + ab a + bc Hướng dẫn 1 a 2 + bc b 2 + ca c2 + ab Xét P = + + 3 3b + 3ca 3c + 3ab 3a + 3bc Ta có 3b + 3ca = b(a + b + c) + 3ca = b(a + b + c) + ca + 2ca mà a 2 + c2 ≥ 2ac nên 3b + 3ca ≤ ab + b 2 + bc + ca + a 2 + c 2 Chứng minh tương tự ta có: 3c + 3ab ≤ ac + c 2 + bc + ab + a 2 + b 2 3a + 3bc ≤ a 2 + ab + ac + bc + c 2 + b 2 1 a 2 + bc + b 2 + ca + c 2 + ab Khi đó P≥ =1 ⇔ P ≥ 3 3 ab + b 2 + bc + ca + a 2 + c2 Dấu “=” xảy ra khi a = b = c = 1. Vậy MinP = 3 khi a = b = c = 1. Bài 16: Cho 3 số dương x, y, z thỏa mãn xy + yz + zx = 3xyz. xy yz zx 3 Chứng minh rằng : 3 3 2 2 + 3 3 2 2 + 3 3 2 2 ≤ x +y +x z+y z y +z +y x+z x z +x +z y+x y 4 Hướng dẫn 1 1 1 Ta có : xy + yz + zx = 3xyz ⇔ + + =3 x y z 1 1 1 1 Với x >0; y > 0; z > 0 ta có x3 + y3 ≥ xy(x + y) ; 2 2 ≤ ( + ) ;x + y ≥ 2xy x+ y 4 x y xy xy xy  1 1  3 3 2 2 ≤ 2 2 ≤  + 2 2  x + y + x z + y z xy(x + y) + (x + y )z 4  xy(x + y) (x + y )z  xy 1 1 xy  1 1 1  ⇒ 3 3 2 2 ≤  + 2 2 ≤  +  x + y + x z + y z 4  (x + y) (x + y )z  4  (x + y) 2z  NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 8
  10. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 1 1  1 1  1  1  1 1  1 ≤   + +  =  + + (1) 4  4  x y  2z  16  x y  8z Chứng minh tương tự : yz 1 1 1 1 ≤  + + (2) y 3 + z3 + y 2 x + z 2 x 16  y z  8x zx 1 1 1 1 3 3 2 2 ≤  + + (3) z + x + z y + x y 16  z x  8y Công (1) ; (2); (3) theo vế ta được đpcm Đẳng thức xảy ra khi x = y = z = 1 Bài 17: Cho các số thực dương x , y, z thỏa mãn 5(x 2 + y 2 + z 2 ) = 9(xy + 2yz + zx ) . x 1 Tìm giá trị lớn nhất của biểu thức P = 22 − . y +z (x + y + z )3 Hướng dẫn Theo giả thiết ta có 5(x 2 + y 2 + z 2 ) = 9(xy + 2yz + zx ) ⇔ 5(x + y + z )2 = 9(xy + 2yz + zx ) + 10(xy + yz + zx ) ⇔ 5(x + y + z )2 = 19x (y + z ) + 28yz ≤ 19x (y + z ) + 7(y + z )2  x  19x x ⇔ 5 + 1 ≤ +7 ⇔ ≤ 2 ⇔ x ≤ 2(y + z )  y + z  y + z y + z 1 Mặt khác ta có (y + z )2 ≤ 2(y 2 + z 2 ) ⇔ y 2 + z 2 ≥ (y + z )2 2 2(y + z ) 1 4 1 Vì vậy P ≤ − 3 = − 1 y + z 27(y + z )3 (y + z )2 ( 2(y + z ) + y + z ) 2 4 1 (6t − 1)2 (2t + 1) Đặt t = y + z > 0 ⇒ P ≤ − =− + 16 ≤ 16 t 27t 3 27t 3  x = 2(y + z )  1  x = Vậy min P = 16 ; dấu bằng đạt tại y = z ⇔  3  1 y = z = 1 y + z =  12  6 x + y +1 Bài 18: Cho các số thực dương x, y thỏa mãn 3 + ln = 9 xy − 3 x − 3 y. 3 xy 3x 3y 1 1 1 Tìm giá trị lớn nhất của biểu thức: M = + + − 2− 2⋅ y ( x + 1) x( y + 1) x + y x y Hướng dẫn Từ giả thiết ta suy ra ln( x + y + 1) + 3( x + y + 1) = ln(3 xy ) + 3.3 xy . NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 9
  11. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 1 Xét hàm số g (t ) = ln t + 3t trên (0; +∞) , ta có g '(t ) = + 3 > 0 với ∀t > 0 , suy ra g (t ) t đồng biến trên (0; +∞) , từ đó g ( x + y + 1) = g (3 xy ) ⇔ x + y + 1 = 3 xy (*) Theo (*) ta có 3 xy − 1 = x + y ≥ 2 xy . Đặt t = xy ⇒ 3t − 2 t − 1 ≥ 0 ⇒ t ≥ 1. 3x 3y 3x 2 ( y + 1) + 3 y 2 ( x + 1) 36t 2 − 27t + 3 + = = . (2) y ( x + 1) x ( y + 1) xy ( xy + x + y + 1) 4t 2 1 1 x2 + y 2 (3t − 1) 2 − 2t −36t 2 + 32t − 4 − − = − = − = (3) x2 y2 x2 y 2 t2 4t 2 1 1 1 5t − 1 1 Theo Cô si ≤ ≤ (4). Từ (2), (3), (4) ta có M ≤ + . x + y 2 xy 2 4t 2 2 5t − 1 Xét hàm số f (t ) = trên [1;+∞) , ta có 4t 2 5.4t 2 − (5t − 1)8t 2 − 5t f '(t ) = = < 0∀t ≥ 1 , suy ra f (t ) nghịch biến trên [1;+∞ ) , bởi vậy 16t 4 4t 3 3 M max = max f (t ) = f (1) = ⇔ t = 1 ⇔ x = y = 1. [1; +∞ ) 2 Bài 19: Cho x, y, z là các số thực dương và thỏa mãn: z ( z − x − y ) = x + y + 1 . x4 y4 36 Chứng minh rằng : ≤ . ( x + yz ).( y + zx ).( z + xy ) 3 4 9 Hướng dẫn Vì z ( z − x − y ) = x + y + 1 ⇒ (z + 1)( x + y) = z2 - 1 và do z > 0 nên ta có: x + y + 1 = z . x4 y4 x4 y4 Khi đó T = = 4 ( x + y ).(1 + y ).( x + y ).(1 + x ). [( x + 1)( y + 1)] 3 ( x + y ) 2 . [( x + 1)( y + 1)] Áp dụng BĐT Côsi cho các số dương x, y ta có : 4 4  3  3 (x + 1) =  x + x + x + 1 ≥  4 4 x  = 4 4 . x ; 4 3 3 3   27  27 4 4  3  3 ( y + 1) =  y + y + y + 1 ≥  4 4 y  = 4 4 . y ; 4 (x + y )2 ≥ 4 xy . 3 3 3   27  27 x 3 .y 3 49 4 4 36 Do đó ( x + y ) 2 . [( x + 1)( y + 1)]4 ≥ 4 xy. 4 8. = . x . y suy ra T ≤ (*) 36 36 49 x y = =1 Dấu “=” ở ( * ) xảy ra ⇔  3 3 ⇔ x = 3, y = 3, z = 7 .  z = x + y + 1 Vậy bất đẳng thức được chứng minh. NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 10
  12. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Bài 20: Cho x, y là hai số thực thỏa mãn điều kiện ( x + y ) 3 + 4 xy ≥ 2 . Tìm giá trị nhỏ nhất của biếu thức P = 3( x 2 + y 2 ) 2 − 2( x + y ) 2 − xy (3xy − 4) + 2015 . Hướng dẫn Với mọi số thực x, y ta luôn có (x + y)2 ≥ 4xy , nên từ điều kiện suy ra ( x + y )3 + ( x + y ) 2 ≥ ( x + y )3 + 4 xy ≥ 2 ⇒ ( x + y )3 + ( x + y )2 − 2 ≥ 0 ⇒ x + y ≥ 1 3 3 Ta biến đổi P như sau P = (x 2 + y 2 ) 2 + (x 2 + y 2 ) 2 − 2(x 2 + y 2 + 2xy) − xy(3xy − 4) + 2015 2 2 3 2 3 = (x + y 2 ) 2 + (x 4 + y 4 ) − 2(x 2 + y 2 ) + 2015 (3) 2 2 4 4 (x 2 + y 2 ) 2 9 Do x + y ≥ nên từ (3) suy ra P ≥ (x 2 + y 2 ) 2 − 2(x 2 + y 2 ) + 2015 2 4 1 Đặt x 2 + y 2 = t thì t ≥ (do x + y ≥ 1) . 2 9 1 9 1 Xét hàm số f (t) = t 2 − 2t + 2015 với t ≥ , có f '(t) = t − 2 > 0 , với t ≥ nên hàm số 4 2 2 2 1   1  32233 f(t) đồng biến trên  ; +∞  . Suy ra min f (t) = f   = . 2  1  t∈ ; +∞  2 16 2  32233 1 Do đó GTNN của P bằng , đạt được khi và chỉ khi x = y = 16 2 Bài 21: Cho a, b, c là độ dài 3 cạnh của một tam giác. a a 2a b c Chứng minh rằng: + + + + < 2. 3a + b 3a + c 2a + b + c 3a + c 3a + b Hướng dẫn +) Vì a, b, c là 3 cạnh của một tam giác nên ta có: a + b > c; b + c > a; c + a > b . a+b c+a +) Đặt x = ;y= ; z = a ( x, y, z > 0). Ta có: x + y > z; y + z > x; z + x > y . 2 2 2a 2x 2y 2z VT = a + c + a + b + = + + = x + y + z (1). 3a + b 3a + c 2a + b + c 2 y + 2 z 2 z + 2 x 2 x + 2 y y + z z + x x + y 2z z Lại có: x + y > z ⇔ z ( x + y + z ) < 2z( x + y ) ⇔ > . x+ y+z x+ y CM tương tự ta có: x < 2 x (2); y < 2 y (3). y+z x+ y+z z+x x+ y+z Từ (1),(2) và (3) ta có x y z 2x + 2 y + 2z ⇒ (đpcm). + + < =2 y+z z+x x+ y x+ y+z NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 11
  13. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Bài 22 : Cho ba số thực dương x, y, z thỏa mãn: xyz = 3. Tìm giá trị nhỏ nhất của biểu thức: P = log32 x + 1 + log32 y + 1 + log32 z + 1 Hướng dẫn NX: những dạng bài có dạng a 2 + b 2 + m 2 + n 2 rất có thể sẽ áp dụng được phương pháp BĐT vec - tơ.         - Trong mp(Oxy), gọi a = (log3 x;1), b = (log3 y;1), c = (log3 z;1) , và n = a + b + c ⇒ n = (1;3)       - Ta có: a + b + c ≥ a + b + c ⇒ log32 x + 1 + log32 y + 1 + log32 z + 1 ≥ 12 + 32    ⇒ P ≥ 10 , dấu = xảy ra khi ba vecto a , b , c cùng hướng và kết hợp điều kiện đề bài ta được x = y = z = 3 3 Vậy minP = 10 khi x = y = z = 3 3 Bài 23: Cho ba số thực a, b, c thỏa: a ∈ [ 0;1] , b ∈ [ 0;2] , c ∈ [ 0;3] . 2 ( 2ab + ac + bc ) 8− b b Tìm giá trị lớn nhất của P = + + 1 + 2a + b + 3c b + c + b (a + c) + 8 12a2 + 3b 2 + 27c 2 + 8 Hướng dẫn Ta có: a ∈ [ 0;1] , b ∈ [ 0;2] , c ∈ [ 0;3] (1 − a )( b + c ) ≥ 0 b + c ≥ ab + ac ⇒ ⇔ ⇒ 2a + b + 3c ≥ 2 ab + bc + ac ( 2 − b )( a + c ) ≥ 0 2a + 2c ≥ ab + bc 2 ( 2ab + ac + bc ) 2 ( 2ab + ac + bc ) ⇒ ≤ 1 + 2a + b + 3c 1 + 2ab + ac + bc Mặt khác b + c ≥ a ( b + c ) ( vì a ∈ [ 0;1] ) 8− b 8− b 8− b ⇒ ≤ = b + c + b ( a + c ) + 8 a ( b + c ) + b ( a + c ) + 8 2ab + bc + ac + 8 Với mọi số thực x, y, z, ta có 2 2 2 ( x − y ) + ( y − z) + ( y − x ) ≥ 0 ⇔ 2 ( x 2 + y 2 + z 2 ) ≥ 2 xy + 2 yz + 2 xz 2 ⇔ 3 ( x 2 + y 2 + z2 ) ≥ ( x + y + z ) 2 2 2 ⇒ 12a2 + 3b2 + 27c 2 = 3 ( 2 a ) + b2 + ( 3c )  ≥ ( 2a + b + 3c ) = 2 a + b + 3c ≥ 2ab + bc + ac   b b => ≤ 12a + 3b + 27c + 8 2ab + bc + ac + 8 2 2 2 Suy ra 2 ( 2ab + bc + ac ) 8−b b P≤ + + 1 + 2ab + bc + ac 2ab + bc + ac + 8 2ab + bc + ac + 8 2 ( 2 ab + bc + ac ) 8 ⇒P≤ + 1 + 2ab + bc + ac 2 ab + bc + ac + 8 Đặt t = 2ab + bc + ac ⇒ t ∈ [ 0;13] NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 12
  14. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 2t 8 Xét hàm số f ( t ) = + , t ∈ [ 0;13] t +1 t + 8 2 8 f '(t) = 2 − 2 , f '(t) = 0 ⇔ t = 6 ( t + 1) ( t + 8) 16 47 16 f ( 0 ) = 1; f ( 6 ) = ; f (13 ) = ⇒ f ( t ) ≤ ∀t ∈ [ 0;13] 7 21 7 16 2 16 16 Do đó: P ≤ . Khi a = 1; b = 2; c = thì P = . Vậy giá trị lớn nhất của P là 7 3 7 7 5 Bài 24: Cho x là số thực thuộc đoạn [ − 1, ] . 4 5 − 4x − 1 + x Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = 5 − 4x + 2 1 + x + 6 Hướng dẫn Đặt a = 5 − 4 x , b = 1 + x thì a 2 + 4b2 = 9, với a, b ≥ 0 π Do đó đặt α ∈ [0, ] với a=3sinα ,2b=3cosα . Khi đó: 2 3 a−b 3sin α − cosα 2 sin α − cosα P= = 2 = a + 2b + 6 3sin α + 3cos α + 6 2 sin α + 2 cos α + 4 2 sin x − cos x π Xét hàm số f ( x ) = với x ∈ [0, ] 2sin x + 2 cos x + 4 2 6 + 4 sin x + 8cos x π Ta có f / ( x ) = > 0, ∀x ∈ [0, ] (2 sin x + 2 cos x + 4) 2 2 π Suy ra hàm số f(x) luôn luôn đồng biến trên [0, ] 2 1 π 1 Do đó: min f ( x ) = f (0) = − ; max f ( x ) = f ( ) = π x∈[0, ] 6 x∈[0,π ] 2 3 2 2 −1 5 Vậy min P = khi x = 6 4 1 Max P = khi x = −1 3 Bài 25: Cho 3 số thực dương a, b, c thoả mãn abc = 1 . a b c Chứng minh rằng: + + ≥ 1. 2+b a 2+c b 2+a c Hướng dẫn a a a Ta có = ≥ , do 1 + a ≥ 2 a . 2 + b a 2 a + ba 1 + a + ba b b c c Tương tự: ≥ ; ≥ . 2 + c b 1 + b + bc 2 + a c 1 + c + ac Cộng các vế của các BĐT trên ta có: NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 13
  15. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 a b c a b c + + ≥ + + 2 + b a 2 + c b 2 + a c 1 + a + ba 1 + b + cb 1 + c + ac abc b cb = + + bc + bca + babc 1 + b + cb b + bc + bac 1 b cb = + + = 1 (điều phải chứng minh). bc + 1 + b 1 + b + cb b + bc + 1 Dấu bằng xảy ra khi và chỉ khi a = b = c = 1 Bài 26: Cho a, b, c là các số thực dương thoả mãn a + b + c = 3 . 2 abc Tìm giá trị lớn nhất của biểu thức P = +3 3 + ab + bc + ca (1 + a )(1 + b )(1 + c ) Hướng dẫn 2 Áp dụng Bất đẳng thức ( x + y + z ) ≥ 3 ( xy + yz + zx ) , ∀x, y, z ∈ ℝ ta có: 2 ( ab + bc + ca ) ≥ 3abc ( a + b + c ) = 9abc > 0 ⇒ ab + bc + ca ≥ 3 abc 3 ( ) Ta có: (1 + a )(1 + b )(1 + c ) ≥ 1 + 3 abc , ∀a, b, c > 0. Thật vậy: (1 + a )(1 + b )(1 + c ) = 1 + ( a + b + c ) + ( ab + bc + ca ) + abc ≥ 3 2 ( 1 + 3 3 abc + 3 3 ( abc ) + abc = 1 + 3 abc ) 3 2 abc Khi đó P ≤ + =Q (1) ( 3 1 + abc ) 1 + 3 abc 3 6 a+b+c Đặt abc = t . Vì a, b, c > 0 nên 0 < abc ≤   =1  3  2 t2 Xét hàm số Q = + , t ∈ ( 0;1] 3 (1 + t 3 ) 1 + t 2 2t ( t − 1) ( t 5 − 1) ⇒ Q '(t ) = ≥ 0, ∀t ∈ ( 0;1] 3 2 2 2 (1 + t ) (1 + t ) 5 Do hàm số đồng biến trên ( 0;1] nên Q = Q ( t ) ≤ Q (1) = ( 2) 6 5 Từ (1) và (2) suy ra P ≤ 6 5 Vậy max P = , đạt được khi và chỉ khi: a = b = c = 1 . 6 Bài 27: Cho 3 số thực x, y, z khác 0 thỏa mãn: x + y + z = 5 và x. y.z = 1 .Tìm giá trị lớn 1 1 1 nhất của biểu thức: P = + + . x y z NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 14
  16. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Hướng dẫn 1 1 1 1 y+z 1 P= + + = + = + x (5 − x) x y z x yz x 2 42 Ta có: ( y + z ) ≥ 4 yz ⇔ ( 5 − x ) ≥ ⇔ x < 0∨ 3− 2 2 ≤ x ≤ 4∨ x ≥ 3+ 2 2 x 1 1 Xét hàm số: f ( x ) = + x ( 5 − x ) ⇒ f ' ( x ) = − 2 + 5 − 2x x x Với: x < 0 ∨ 3 − 2 2 ≤ x ≤ 4 ∨ x ≥ 3 + 2 2 1 f ' ( x) = 0 ⇔ x = ∨ x = 1 − 2 ∨ x = 1 + 2 2 Lập bảng biến thiên đúng Tính được: ( ) ( ) f 1− 2 = f 3 + 2 2 = 1− 4 2 f (1 + 2 ) = f ( 3 − 2 2 ) = 1 + 4 2 Vậy giá trị lớn nhất của P bằng 1 + 4 2 Dấu “=” khi : x = y = 1 + 2, z = 3 − 2 2 hay x = z = 1 + 2, y = 3 − 2 2 hoặc x = y = 3 − 2 2, z = 1 + 2 hay x = z = 3 − 2 2, y = 1 + 2 Bài 28: Cho x, y, z là các số thực dương. 2 3 Tìm giá trị nhỏ nhất của biểu thức P = − 3 x + xy + xyz x+ y+z Hướng dẫn 1 1 Ta có x + xy + 3 xyz = x + 2 x.8 y + 3 2 x.8 y.32 z 4 8 2 x + 8 y 2 x + 8 y + 32 z 32 4 ≤ x+ + = (x + y + z) = (x + y + z) 8 24 24 3 3 2 Đặt t = x + y + z ; t ≥ 0 ⇒ P ≥ f ( t ) = 2 − 2t 3t 3 1 f ′ (t ) = − 3 + 2 ; f ′ (t ) = 0 ⇔ t = 1 t t 3 Lập bảng biến thiên của hàm f(t) ta được Pmin = − tại t=1 2  16  x = 21 x + y + z = 1    4 Dấu “=” xảy ra khi và chỉ khi 2 x = 8 y ⇒ y = 2 x = 32 z  21   1  z = 21  Bài 29: Cho a, b, c không âm và a 2 + b 2 + c 2 = 3 . Tìm giá trị lớn nhất của biểu thức P = ab + bc + ca + 5a + 5b + 5c + 4 Hướng dẫn NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 15
  17. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 2 Ta có 3 ≤ ( a + b + c ) ≤ 3 ( a 2 + b2 + c 2 ) 2 ⇔ 3 ≤ (a + b + c) ≤ 9 ⇔ 3 ≤ a+b+c ≤3 Đặt t = a + b + c với t ∈  3; 3 2 (a + b + c) − ( a 2 + b2 + c2 ) t2 − 3 Mà ab + bc + ca = = 2 2 1 5 Nên P ( t ) = t 2 + 5t + . P ' ( t ) = t + 5 > 0, ∀t ∈  3; 3 . Lập BBT ta có kết quả. 2 2 Vậy Pmax = 22 với t = 3 ⇔ a = b = c = 1 Bài 30: Cho các số thực a, b, c thỏa mãn a ≥ b ≥ c và a 2 + b 2 + c 2 = 5 . Chứng minh rằng: (a − b)(b − c)(c − a)(ab + bc + ca) ≥ −4 Hướng dẫn Ta có: (a − b)(b − c)(c − a)(ab + bc + ca) ≥ −4 ⇔ P = (a − b)(b − c)(a − c)(ab + bc + ca ) ≤ 4 Do a ≥ b ≥ c nên Nếu ab + bc + ca < 0 thì P ≤ 0 < 4 (đúng) Nếu ab + bc + ca ≥ 0 thì đặt ab + bc + ca = x ≥ 0 (a − c) 2 Áp dụng BĐT Côsi : (a − b)(b − c) ≤ 4 (a − c) 3 ⇒ (a − b)(b − c)(a − c) ≤ (1) 4 Áp dụng BĐT Bunhiacopski: 2[(a − b) 2 + (b − c) 2 ] ≥ (a − c) 2 và 4(a 2 + b 2 + c 2 − ab − bc − ca) = 2(a − b) 2 + 2(b − c) 2 + 2(a − c) 2 ⇒ 4(a 2 + b 2 + c 2 − ab − bc − ca ) ≥ (a − c) 2 + 2(a − c) 2 ⇔ 4(5 − x) ≥ 3(a − c) 2 ≥ 0 2 5− x ⇒ x ≤ 5 va ɳ a − c ≤ ( 2) 3 Từ (1) và (2) ta có: (a − c) 3 2 3 P≤ .x ≤ x (5 − x) 3 4 9 Xét hàm số f ( x) = x (5 − x) 3 ; x ∈ [0;5] 5 x = 2 f ' ( x) = 5 − x (5 − x) ; f ' ( x) = 0 ⇔  2 x = 5 Ta có: f (0) = 0 ; f ( 2) = 6 3 ; f (5) = 0 NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 16
  18. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Max f ( x) = 6 3 ⇒ f ( x) = x (5 − x) 3 ≤ 6 3 ; ∀x ∈ [0;5] [0;5 ] 2 3 ⇒P≤ .6 3 ⇔ P ≤ 4 9 x = 2 ab + bc + ca = 2 a − b = b − c b = a − 1 a = 2    Dấu "=" xảy ra ⇔  ⇔ ⇔ b = 1  a − c = 2  c = a − 2 c = 0 a 2 + b 2 + c 2 = 5 a 2 + b 2 + c 2 = 5  Bài 31:Cho các số thực dương x, y, z. yz zx xy Tìm giá trị lớn nhất của biểu thức P = + + x + 2 yz y + 2 zx z + 2 xy Hướng dẫn Áp dụng bất đẳng thức AM – GM ta có 2 yz x x = 1− ≤ 1− (1) x + 2 yz x + 2 yz x+ y+z 2 zx y y Tương tự ta có = 1− ≤ 1− (2) y + 2 zx y + 2 zx x+ y+z 2 xy z z = 1− ≤ 1− (3) z + 2 xy z + 2 xy x+ y+z Cộng 3 bất đẳng thức cùng chiều (1), (2), (3) ta được 2 P ≤ 2 ⇔ P ≤ 1 Dấu bằng xảy ra khi x = y = z. Vậy Max P = 1 khi x = y = z. Bài 32: Cho bốn số dương a, b, c, d thoả mãn a + b + c + d = 4 a b c d Chứng minh rằng: + + + ≥2 1 + b2 c 1 + c2 d 1 + d 2a 1 + a2 b Hướng dẫn NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 17
  19. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 Sử dụng bất đẳng thức Cô–si: a ab2 c ab2 c ab c ab(1 + c) ab abc =a− ≥a− =a− ≥a− =a− − (1) 1+b c 2 1+ b c 2 2b c 2 4 4 4 Dấu = xảy ra khi và chỉ khi b = c = 1 b bc 2 d bc 2 d bc d bc (1 + d ) bc bcd =b− ≥b− =b− ≥b− =b− − (2) 1+c 2 d 1 + c2 d 2c d 2 4 4 4 c cd 2 a cd 2 a cd a cd (1 + a ) cd cda =c− ≥c− =c− ≥c− =c− − (3) 1+d a 2 1+ d a 2 2d a 2 4 4 4 d da2 b da2 b da b da (1 + b ) da dab =d− ≥d− =d− ≥d− =d− − (4) 1+a 2 b 1 + a2 b 2a b 2 4 4 4 Từ (1), (2), (3), (4) suy ra: a b c d ab + bc + cd + da abc + bcd + cda + dab + + + ≥4− − 1+ b c 2 1+ c d2 1+ d a 2 1+ a b 2 4 4 Mặt khác: 2 a+c+b+d  • ab + bc + cd + da = ( a + c )( b + d ) ≤   =4 .  2  Dấu "=" xảy ra ⇔ a+c = b+d 2 2 a+b c+d • abc + bcd + cda + dab = ab ( c + d ) + cd ( b + a ) ≤   (c + d ) +   (b + a)  2   2  a+b c+d ⇔ abc + bcd + cda + dab ≤ ( a + b )( c + d )  +  = ( a + b )( c + d )  4 4  2 a+b+c+d  ⇔ abc + bcd + cda + dab ≤   = 4 . Dấu "=" xảy ra ⇔ a = b = c = d = 1.  2  a b c d 4 4 Vậy ta có: + + + ≥4− − 1 + b2 c 1 + c2 d 1 + d 2 a 1 + a2 b 4 4 a b c d ⇔ + + + ≥ 2 ⇒ đpcm. 2 2 2 1+ b c 1+ c d 1+ d a 1 + a2 b Dấu "=" xảy ra khi và chỉ khi a = b = c = d = 1. 5 Bài 33: Cho a,b là hai số thực dương thỏa 2a + b = . 4 2 1 Tìm giá trị nhỏ nhất của biểu thức F = + a 4b Hướng dẫn 2 1 2 1 2 1 Ta có : F = + = + 8a + + 4b − (8a + 4b) = + 8a + + 4b − 5 a 4b a 4b a 4b 2 1 Bất đẳng thức Côsi cho : + 8a ≥ 8 và + 4b ≥ 2 a 4b NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 18
  20. TUYỂN TẬP 50 BÀI TOÁN ĐIỂN HÌNH VỀ MIN - MAX TRONG CÁC ĐỀ THI THỬ THPT QUỐC GIA 2015 2  a = 8a   1  1 = 4b a = 2 Suy ra F ≥ 5 . MinF = 5 đạt khi  4b ⇔  5 b = 1 2a + b =  4  4 a, b > 0 Bài 34: Cho x,y ∈ R và x, y > 1. Tìm giá trị nhỏ nhất của P = (x 3 + y3 ) − ( x2 + y 2 ) ( x − 1)( y − 1) Hướng dẫn t2 Đặt t = x + y ; t > 2. Áp dụng BĐT 4xy ≤ (x + y)2 ta có xy ≤ 4 t 3 − t 2 − xy (3t − 2) t2 P= . Do 3t - 2 > 0 và − xy ≥ − nên ta có xy − t + 1 4 t 2 (3t − 2) t3 − t 2 − 4 t2 P≥ = t2 t−2 − t +1 4 t2 t 2 − 4t Xét hàm số f (t ) = ; f '(t ) = ; f’(t) = 0 ⇔ t = 0 v t = 4. t−2 (t − 2) 2 t 2 4 +∞ f’(t) - 0 + +∞ +∞ f(t) 8 x + y = 4 x = 2 Do đó min P = min f (t ) = f(4) = 8 đạt được khi  ⇔ (2;+∞ )  xy = 4 y = 2 Bài 35: Cho các số thực dương a,b,c đôi một khác nhau thỏa mãn 2a ≤ c và ab + bc = 2c 2 . a b c Tìm giá trị lớn nhất của biểu thức P = + + . a−b b−c c−a Hướng dẫn a 1 a b b a 2c ≤ ; ab + bc = 2c 2 ⇔ . + = 2 ⇔ = Theo giả thiết: 2a ≤ c nên −1 c 2 c c c c b a 1 b 4 c 3 Vì ≤ nên ≥ . Đặt t = thì 0 < t ≤ c 2 c 3 b 4 a b 1 2t 2 − t 1 1 2 7 P= c + c + = 2 + + = 1− + a b b a 2t − t − 1 1 − t 2(1 − t ) 2t + 1 6(1 − t ) − −1 1− c c c c NGUYỄN HỮU BIỂN - https://www.facebook.com/groups/nguyenhuubien Trang 19
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
7=>1