1
CÂU HỎI, ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
MÔN: XỬ LÝ TÍN HIỆU SỐ
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 1
Bài 1.1
Cho tín hiệu tương tự
()
ttttxa
π
π
π
100cos300sin1050cos3
−
+=
Hãy xác định tốc độ lấy mẫu Nyquist đối với tín hiệu này?
Bài 1.2
Cho tín hiệu
(
)
ttxa
π
100cos3=
a) Xác định tốc độ lấy mẫu nhỏ nhất cần thiết để khôi phục tín hiệu ban đầu.
b) Giả sử tín hiệu được lấy mẫu tại tốc độ 200
=
s
F Hz. Tín hiệu rời rạc nào sẽ có được
sau lấy mẫu?
Bài 1.3
Tìm quan hệ giữa dãy nhảy đơn vị u(n) và dãy xung đơn vị
(
)
n
δ
Bài 1.4
Tương tự bài trên tìm quan hệ biểu diễn dãy chữ nhật rectN(n) theo dãy nhảy đơn vị u(n).
Bài 1.5
Hãy biểu diễn dãy
()
1n
δ
+
Bài 1.6
Xác định x(n) = u(n-5)-u(n-2)
Bài 1.7
Xác định năng lượng của chuỗi
() ()
⎪
⎩
⎪
⎨
⎧
<
≥
=03
021 2
n
n
nx n
Bài 1.8
Hãy xác định năng lượng của tín hiệu
()
nj
Aenx 0
ω
=
Bài 1.9
Xác định công suất trung bình của tín hiệu nhảy bậc đơn vị u(n)
2
Bài 1.10
Xác định công suất trung bình của tín hiệu nhảy bậc đơn vị u(n)
Bài 1.11
Hãy xác định công suất trung bình của tín hiệu
()
nj
Aenx 0
ω
=
Bài 1.12
Đáp ứng xung và đầu vào của một hệ TTBB là:
()
1n 1
2n0
hn 1n1
1n2
0
=
−
⎧
⎪
=
⎪
⎪
==
⎨
⎪−=
⎪≠
⎪
⎩n
()
1n0
2n1
xn 3n2
1n3
0
=
⎧
⎪
⎪
⎪
=
=
⎨
⎪
=
⎪
≠
⎪
⎩n
Hãy xác định đáp ứng ra y(n) của hệ.
Bài 1.13
Tương tự như bài trên hãy tính phép chập x3(n) = x1(n)*x2(n) với:
a) x1(n) = 10
3
0
nn
n
⎧−≥
⎪
⎨
⎪≠
⎩
; x2(n) = rect2(n-1).
b) x1(n) =
()
1n
δ
+
+
()
2n
δ
−; x2(n) = rect3(n).
Bài 1.14
Cho HTTT bất biến có h(n) và x(n) như sau:
()
0
0
n
an
hn n
⎧≥
=⎨≠
⎩
()
0
0
n
bn
xn n
⎧≥
=⎨
≠
⎩
0 < a < 1, 0 < b < 1, a ≠ b. Tìm tín hiệu ra (đáp ứng ra)?
Bài 1.15
Hãy xác định xem các hệ có phương trình mô tả quan hệ vào ra dưới đây có tuyến tính
không:
a)
() ()
nnxny =
b)
() ()
nxny 2
=
Bài 1.16
Hãy xác định xem các hệ có phương trình mô tả quan hệ vào ra dưới đây có tuyến tính
không:
a)
()
(
)
2
nxny =
b)
() ()
BnAxny +=
3
Bài 1.17
Xác định xem các hệ được mô tả bằng những phương trình dưới đây là nhân quả hay không:
a)
() () ( )
1−
−
=nxnxny
b)
() ()
naxny =
Bài 1.18
Xác định xem các hệ được mô tả bằng những phương trình dưới đây là nhân quả hay không:
a)
() () ( )
43 ++= nxnxny ;
b)
()
(
)
2
nxny =;
c)
() ( )
nxny 2=;
d)
() ( )
nxny −=
Bài 1.19
Xét tính ổn định của hệ thống có đáp ứng xung h(n) = rectN(n).
Bài 1.20
Xác định khoảng giá trị của a và b để cho hệ TT BB có đáp ứng xung
()
⎩
⎨
⎧
<
≥
=0
0
nb
na
nh n
n
là ổn định.
Bài 1.21.
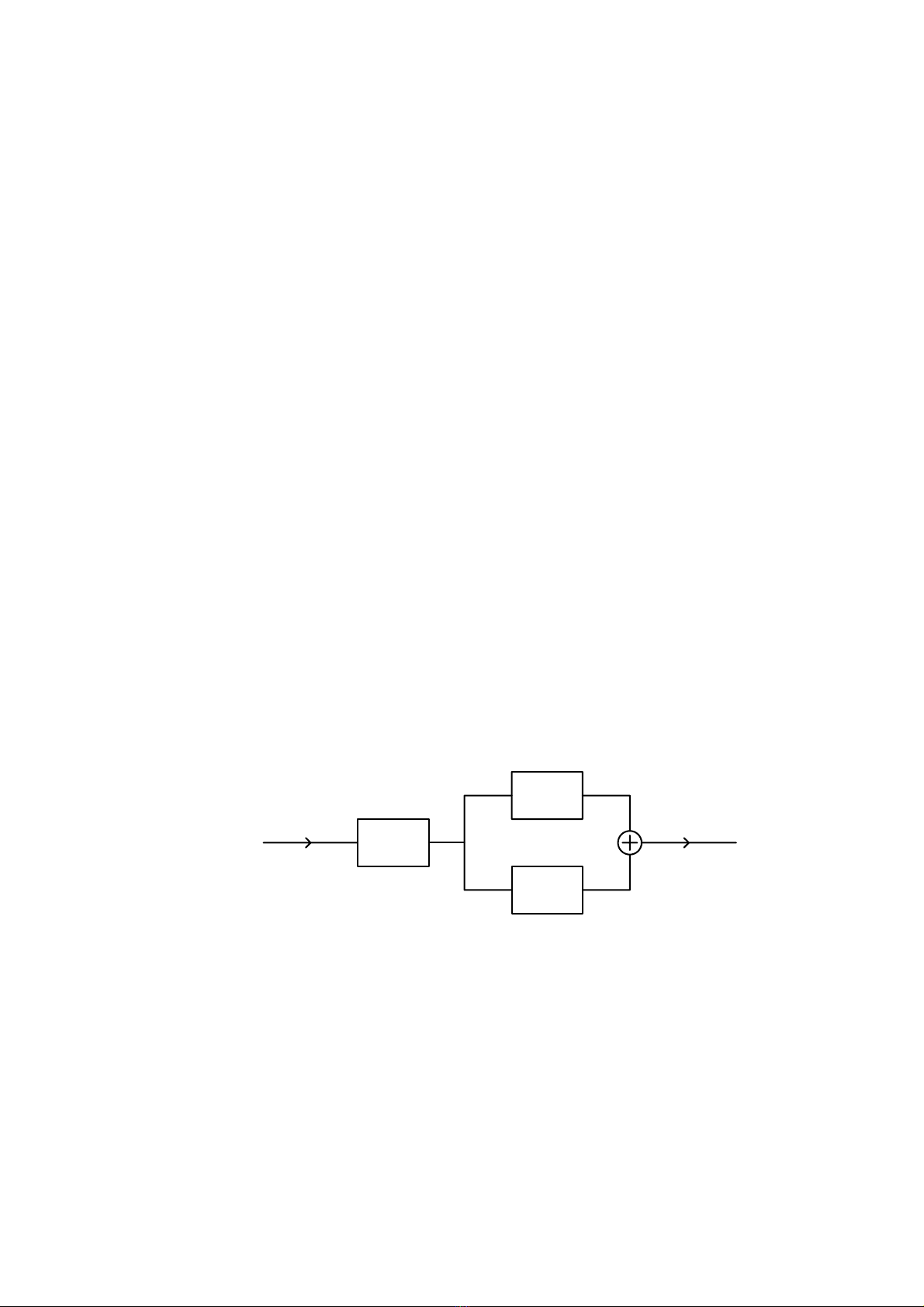
Hãy tìm đáp ứng xung h(n) của một hệ thống số được cho bởi sơ đồ sau đây:
x(n)
(
)
2
hn
(
)
3
hn
y(n)
(
)
1
hn
Bài 1.22
Cho một hệ thống tuyến tính bất biến được mô tả bằng phương trình sai phân sau đây:
() () ( )
(
)
(
)
01 2 4
124yn bxn bxn bxn bxn=+−+−+−
Hãy biểu diễn hệ thống đó.
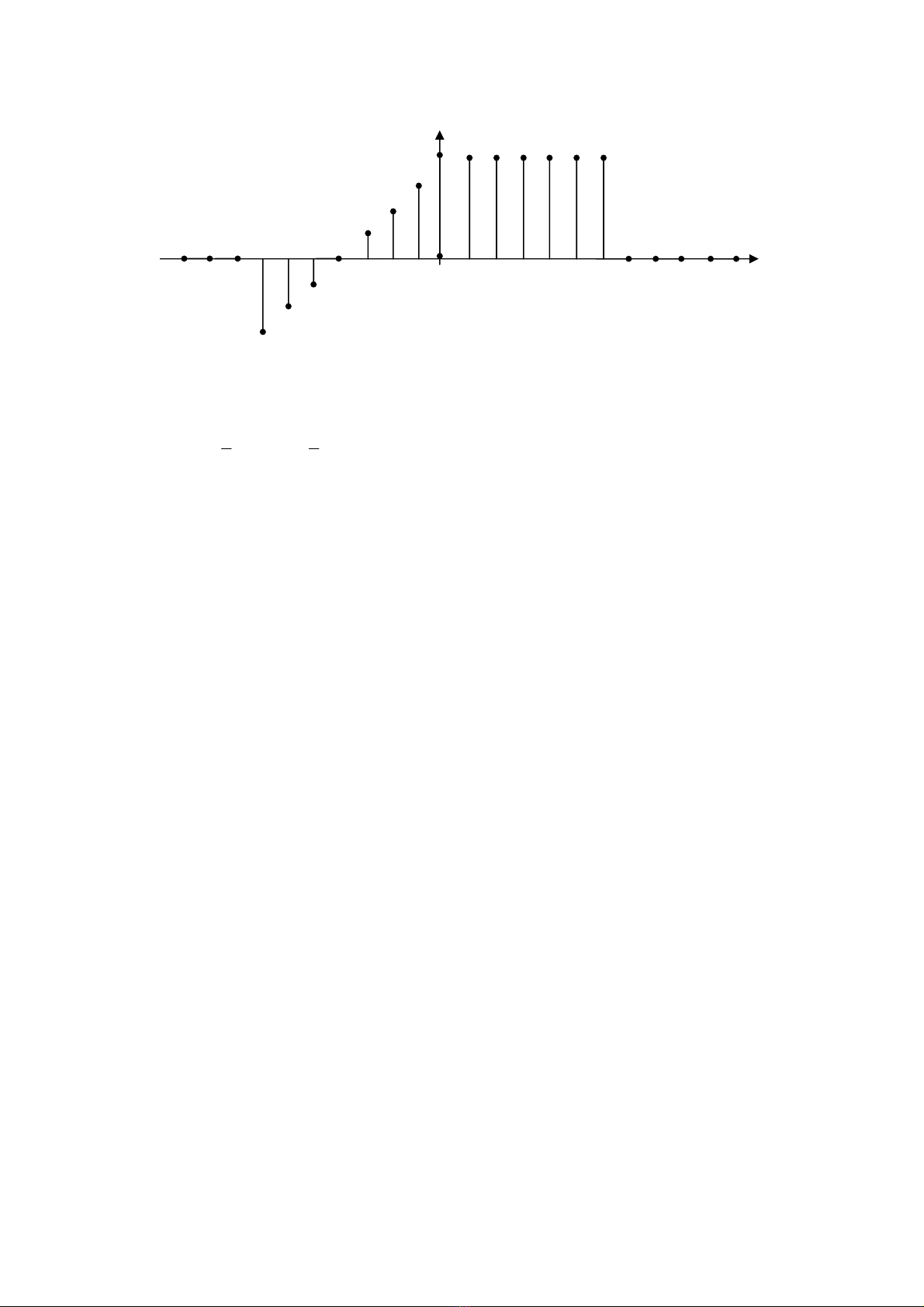
Bài 1.23
Hãy biểu diễn bằng đồ thị tín hiệu
(
)
(
)
nxny 2
=
, ở đây
(
)
nx là tín hiệu được mô tả như
sau:.
4
Bài 1.24
Hãy xác định nghiệm riêng của phương trình sai phân.
()
)()2()1( 6
1
6
5nxnynyny +−−−=
khi hàm cưỡng bức đầu vào
()
0,2 ≥= nnx n và bằng không với n khác.
Bài 1.25
Hãy giải phương trình sai phân tuyến tính hệ số hằng sau
y(n) – 3y(n-1) + 2y(n-2) = x(n) + x(n-2)
Với điều kiện đầu y(-1) = y(-2) = 0 và x(n) = 5 n
Bài 1.26
Cho x(n) = rect3(n)
Hãy xác định hàm tự tương quan Rxx(n).
Bài 1.27
Hãy cho biết cách nào sau đây biểu diễn tổng quát một tín hiệu rời rạc bất kỳ x(n)?
a) () ()( )
k
x
nxnnk
δ
+∞
=−∞
=−
∑ b)
0
() ()( )
k
x
nxknk
δ
+∞
=
=
−
∑
c) () ()( )
k
x
nxknk
δ
+∞
=−∞
=−
∑ d)
() ()( )
k
x
nxnkn
δ
+∞
=−∞
=
−
∑
Bài 1.28
Hệ thống được đặc trưng bởi đáp ứng xung h(n) nào sau đây là hệ thống nhân quả:
a) h(n) = u(n+1) b) h(n) = -u(n-1)
c) h(n) = -u(-n-1) d) h(n) = -u(n+1)
Bài 1.29
Phép chập làm nhiệm vụ nào sau đây:
a) Phân tích một tín hiệu ở miền rời rạc b) Xác định đáp ứng ra của hệ thống
-7 -6 -5 -4
-3 -2 -1 0 1 2 3 4 5 6 n
(
)
nx
4
5
c) Xác định công suất của tín hiệu d) Xác định năng lượng tín hiệu
Bài 1.30
Phương trình sai phân tuyến tính hệ số hằng mô tả hệ thống rời rạc nào sau đây:
a) Hệ thống tuyến tính bất biến. b) Hệ thống tuyến tính.
c) Hệ thống ổn định. d) Hệ thống bất biến.
ĐÁP ÁN CHƯƠNG I
Bài 1.1.
Do 2.
f
ω
π
=, tín hiệu trên có các tần số thành phần sau:
25
1=F Hz, 150
2=F Hz, 50
3
=
F Hz
Như vậy, 150
max =F Hz và theo định lý lấy mẫu ta có:
max
2 300
s
FF≥= Hz
Tốc độ lấy mẫu Nyquist là max
2FFN
=
. Do đó, 300
=
N
F Hz.
Bài 1.2
a) Tần số của tín hiệu tương tự là 50
=
F Hz. Vì thế, tốc độ lấy mẫu tối thiểu cần thiết để
khôi phục tín hiệu, tránh hiện tượng chồng mẫu là 100
=
s
F Hz.
b) Nếu tín hiệu được lấy mẫu tại 200
=
s
F Hz thì tín hiệu rời rạc có dạng
() ()
(
)
nnnx 2cos3200100cos3
π
π
=
=
Bài 1.3
Theo định nghĩa dãy nhảy đơn vị u(n) và dãy xung đơn vị
(
)
n
δ
ta có:
()
()
n
k
un k
δ
=−∞
=∑
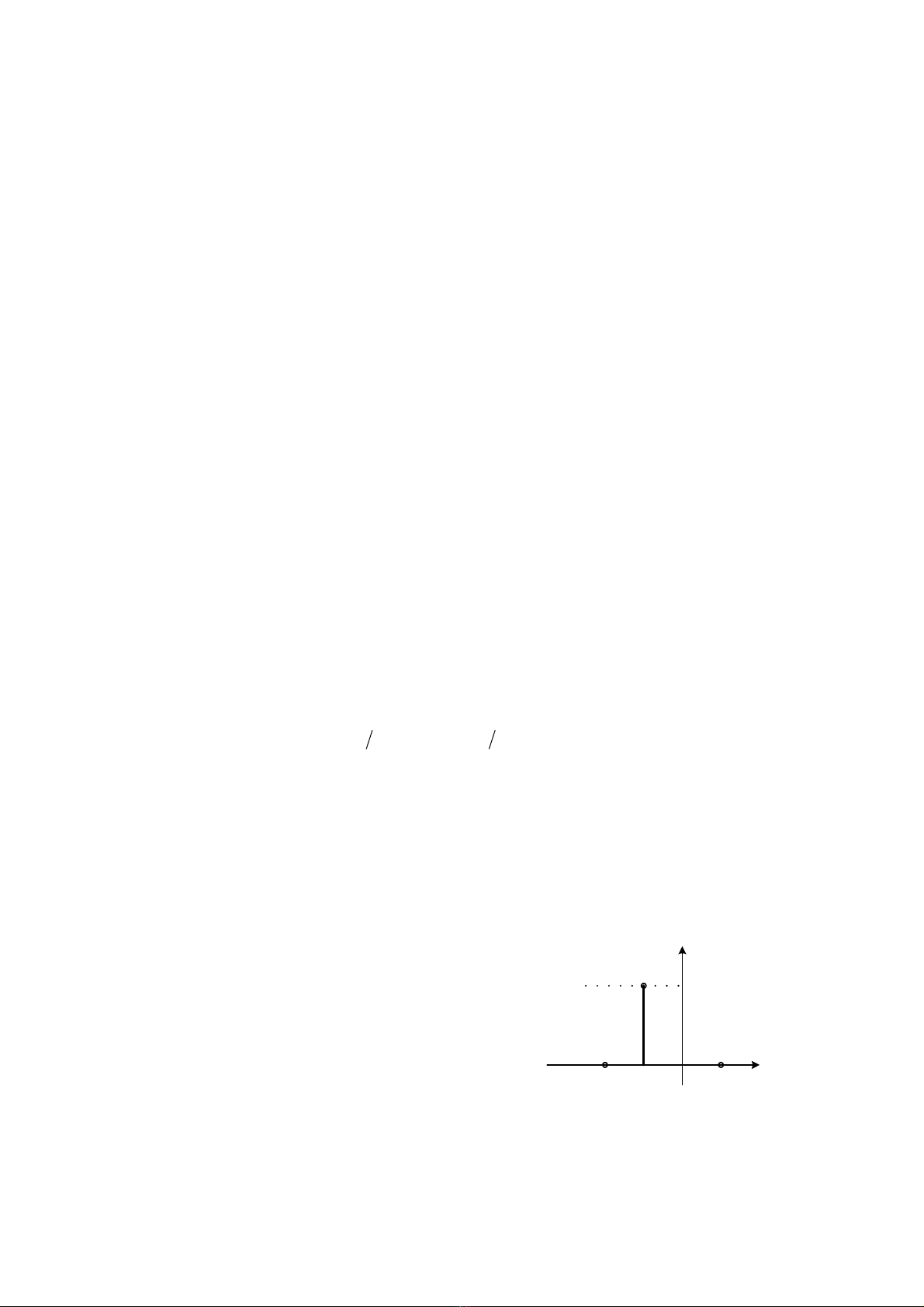
Bài 1.5
Ta có:
()
110 1
100
nn
nn
δ
+= → =−
⎧
+=
⎨≠
⎩
1
-1 0
()
1n
δ
+
n
1-2