GIÁO DỤC HỒNG PHÚC
Phú Thọ, 09/2011
(CÓ ĐÁP ÁN CHI TIẾT)
GV: Lưu Huy Thưởng
GIÁO DỤC HỒNG PHÚC
Chuyên luyện thi đại học khối A + B
Trụ sở : Thị trấn Hùng Sơn _ Lâm Thao _ Phú Thọ
Cơ sở 2 : Tứ Xã - Lâm Thao - Phú Thọ
Cơ sở 3 : Thị trấn Lâm Thao - Lâm Thao - Phú Thọ
Điện thoại: 02106.259.638
Bieån
hoïc
meânh
moâng,
laáy
chuyeân
caàn
laøm
beán!
Maây
xanh
khoâng
loái,
laáy
chí
caû
döïng
leân!
GV: Lưu Huy Thưởng 0913.283.238
GIÁO DỤC HỒNG PHÚC - NƠI KHỞI ĐẦU ƯỚC MƠ
1
PHẦN I: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Câu 1. Cho hàm số
y m x mx m x
3 2
1
3
(1)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi
m
2
.
2) Tìm tất cả các giá trị của tham số m để hàm số (1) đồng biến trên tập xác định của nó.
Giải
Tập xác định: D = R. y m x mx m
2
( 1) 2 3 2
.
(1) đồng biến trên R
y x
0,
2
2
2
( 1) 2 3 2 0,
1 2 0 1
3 2 0 11
2
1 0 2 5 2 0 2
2
( 1)(3 2) 0
m x mx m x
m m m
mmm
m
mm m m
m m m
Câu 2. Cho hàm số y x x mx
3 2
3 4
(1)
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi
m
0
.
2) Tìm tất cả các giá trị của tham số m để hàm số (1) đồng biến trên khoảng
( ;0)

.
Giải
Tập xác định: D =
;
2
' 3 6
y x x m
,
(1) đồng biến trên khoảng (-
;0)
y’
0,
x
(-
;0)
2
3 6 0
x x m
x
(-
;0)
2
3 6
x x m
x
(-
;0)
Xét hàm số f(x) =
2
3 6
x x m
trên (-
;0]
Có f’(x) = 6x + 6; f’(x) = 0
x = -1
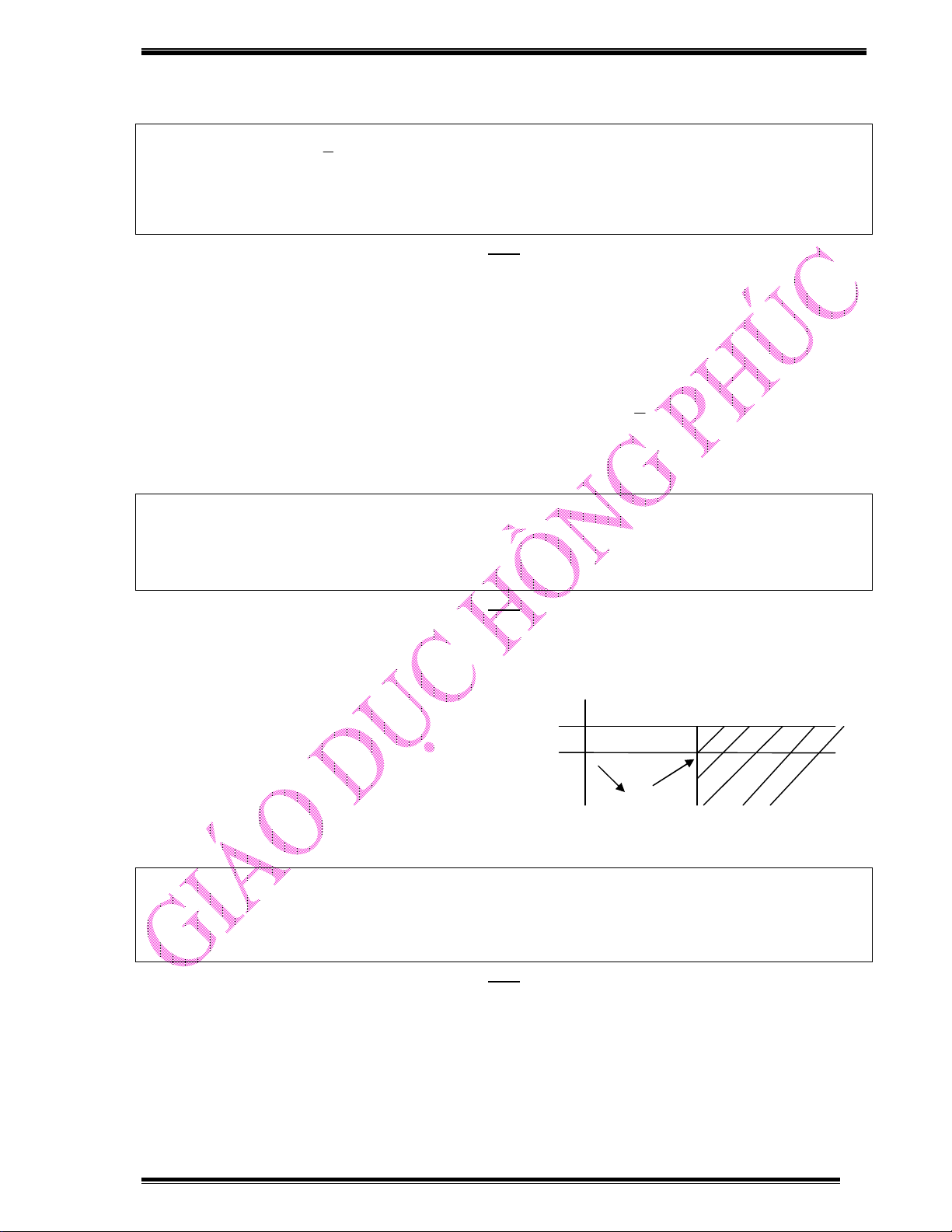
Từ bảng biến thiên:
m
3
Câu 3. Cho hàm số
y x m x m m x
3 2
2 3(2 1) 6 ( 1) 1
có đồ thị (Cm).
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 0.
2) Tìm m để hàm số đồng biến trên khoảng
(2; )

Giải
Tập xác định: D =
y x m x m m
2
' 6 6(2 1) 6 ( 1)
có m m m
2 2
(2 1) 4( ) 1 0
x m
yx m
' 0
1
Ta có: y’
0,
x (-
;m) và (m + 1; +
)
Do đó: hàm số đồng biến trên
(2; )

m
1 2
m
1
+
-
-
+
-3
0
x
f’(x)
x
f(x)
-
+
0 -1
GV: Lưu Huy Thưởng 0913.283.238
GIÁO DỤC HỒNG PHÚC - NƠI KHỞI ĐẦU ƯỚC MƠ
2
Câu 4. Cho hàm số3 2
(1 2 ) (2 ) 2
y x m x m x m
.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
2) Tìm m để hàm đồng biến trên
0;

.
Giải
Tập xác định: D =
2
3 (1 2 (2
) 2 )
y x m x m
Hàm đồng biến trên
(0; )

y x m x m
2
3 (1 2 ) (22
) 0
với
x
0 )
(
;

x
f x m
x
x
223
( )
4 1
2
với
x
0 )
(
;

Ta có:
22
2
2(2
( ) 0 2
(4
1
)1
1
1) 0
1
2
x
xxx
x
f x x
x
Lập bảng biến thiên của hàm
f x
( )
trên
(0; )

, từ đó ta đi đến kết luận:
1 5
2 4
f m m
Câu 5. Cho hàm số 4 2
2 3 1
y x mx m
(1), (m là tham số).
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1.
2) Tìm m để hàm số (1) đồng biến trên khoảng (1; 2).
Giải
Tập xác định: D =
Ta có 3 2
' 4 4 4 ( )
y x mx x x m
+
0
m
,
0,
y x
0
m
thoả mãn.
+
0
m
,
0
y có 3 nghiệm phân biệt:
, 0,
m m
.
Hàm số (1) đồng biến trên (1; 2) khi chỉ khi
1 0 1
m m . Vậy
;1
m

.
Câu 6. Cho hàm số mx
y
x m
4
(1)
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi
m
1
.
2) Tìm tất cả các giá trị của tham số m để hàm số (1) nghịch biến trên khoảng
( ;1)

.
Giải
Tập xác định: D = R \ {–m}. m
y
x m
2
2
4
( )
.
Hàm số nghịch biến trên từng khoảng xác định
y m
0 2 2
(1)
Để hàm số (1) nghịch biến trên khoảng
( ;1)

thì ta phải có
m m
1 1
(2)
Kết hợp (1) và (2) ta được:
m
2 1
.
GV: Lưu Huy Thưởng 0913.283.238
GIÁO DỤC HỒNG PHÚC - NƠI KHỞI ĐẦU ƯỚC MƠ
3
Câu 7. Chứng minh rằng, hàm số 2
sin cos
y x x
đồng biến trên đoạn
0;
3
và nghịch biến trên
đoạn
;
3
Giải
Hàm số đã cho xác định trên
0;
Ta có:
' sin (2cos 1), (0; )
y x x x
Vì
(0; ) sin 0
x x
nên trên
1
(0; ) : ' 0 cos
2 3
y x x
+ Trên khoảng
0; : ' 0
3y
nên hàm số đồng biến trên đoạn
0;
3
+ Trên khoảng
; : ' 0
3y
nên hàm số nghịch biến trên đoạn
;
3
Câu 8. Cho hàm số 3 2
3
y x x mx m
. Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 1
Giải
Hàm số đã cho xác định trên
Ta có: 2
' 3 6
y x x m
có
' 9 3
m
+ Nếu m
3 thì y’
0,
x
, khi đó hàm số đồng biến trên
, do đó m
3 không thỏa mãn.
+ Nếu m < 3, khi đó: y’ = 0 có hai nghiệm phân biệt
1
x
,
2
x
1 2
( )
x x
và hàm số nghịch biến
trong đoạn:
1 2
;
x x
với độ dài l =
2 1
x x
Theo Vi-ét ta có: 1 2 1 2
2,
3
m
x x x x
Hàm số nghịch biến trên đoạn có độ dài bằng 1
l = 1
22
2 1 1 2 1 2
4 9
1 ( ) 4 1 4 1
3 4
x x x x x x m m