ĐẠO HÀM VÀ VI PHÂN.
( DERIVATIVE AND DIFFERENTIATION )
ĐẠO HÀM TẠI 1 ĐIỂM
Cho y = f (x) xác định trong (a, b) x0, xét tỷ số
0 0 0 0
0
( ) ( ) ( ) ( ) ( )f x f x f x f x x f x
x x x x
Nếu tỷ số trên có giới hạn hữu hạn khi x →x0 hay x → 0 thì
f có đạo hàm (derivative) tại x0.
0
0
0
( 0)
( )
( ) lim
x x
x
f x
f x x
: ,x increment of argument:f increment of function
Công thức đạo hàm hàm một biến
1
2
2
ln
1
ln
sin cos
cos sin
1
tan 1 tan
cos
x x
x x
a a a
e e
xx
x x
x x
x x
x x
x

Công thức đạo hàm hàm một biến
2
2
2
2
1
arcsin 1
1
arccos 1
1
arctan 1
1
arccot 1
x
x
x
x
xx
x


2
2
cosh sinh
sinh cosh
1
tanh cosh
1
coth sinh
x x
x x
xx
xx

0
( )
tan f x
x
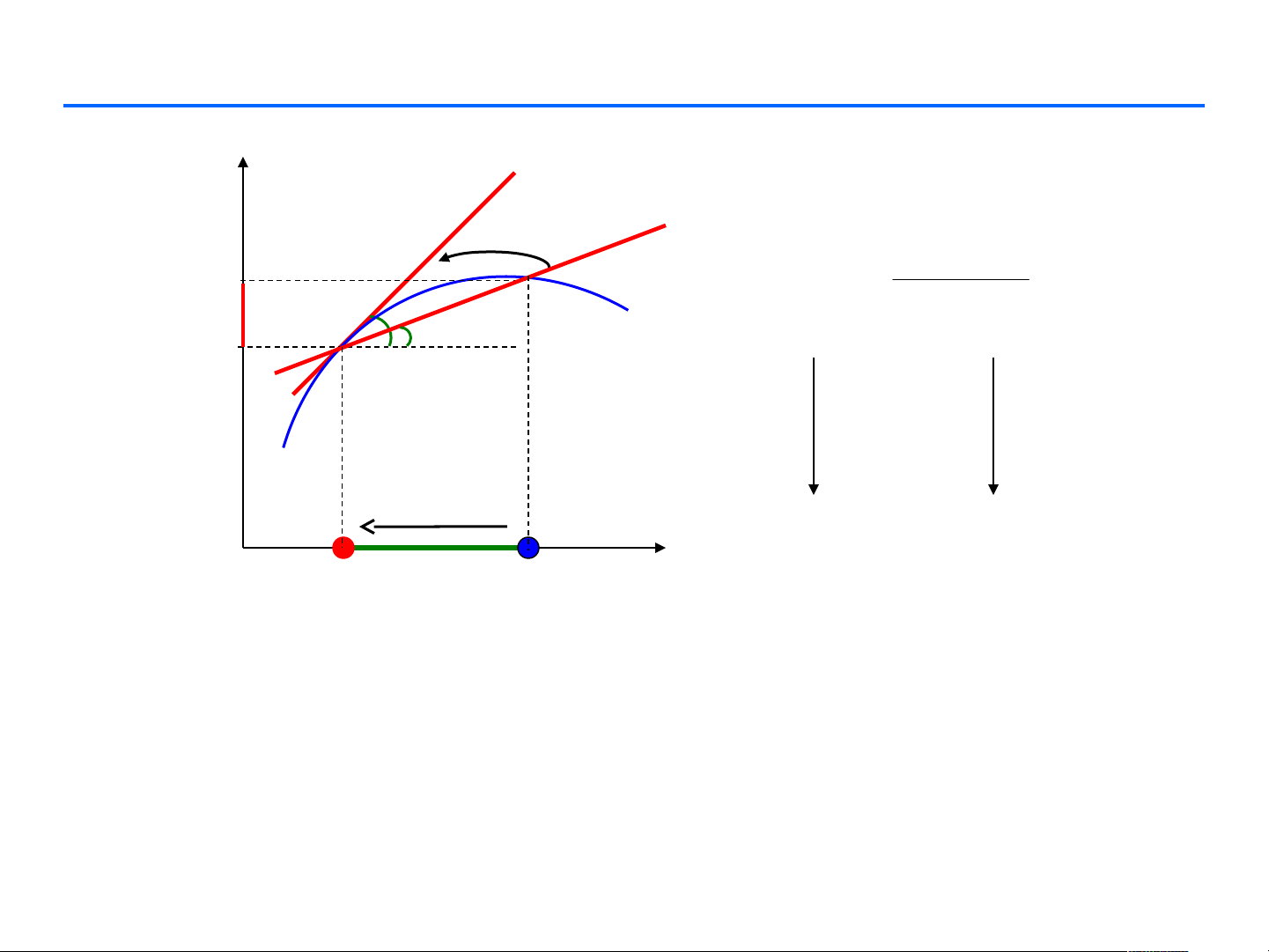
Ý nghĩa hình học của đạo hàm
0
tan ( )f x
x x0
f (x0) là hệ số góc (slope) tiếp tuyến (tangent line) của đường
cong (C): y = f (x) tại tiếp điểm M(x0, f (x0))
x
f (x0)
x0x