Cấu trúc tinh thể
Trong khoáng vật học và tinh thể học, một cấu trúc tinh thể là một sự sắp xếp đặc biệt
của các nguyên tử trong tinh thể. Một cấu trúc tinh thể gồm có một ô đơn vị và rất nhiều
các nguyên tử sắp xếp theo mộ
Cấu trúc và đối xứng của tinh thể có vai trò rất quan trọng với các tính chất liên kết, tính
chất điện, tính chất quang,... của của tinh thể.
Ô đơn vị
Ô đơn vị là một cách sắp xếp của các nguyên tử trong không gian ba chiều, nếu ta lặp lại
nó thì nó sẽ chiếm đầy không gian và sẽ tạo nên tinh thể. Vị trí của các nguyên tử trong ô
đơn vị được mô tả bằng một hệ đơn vị hay còn gọi là một hệ cơ sở bao gồm ba thông số
tương ứng với ba chiều của không gian (x,y,z)
i i i .
Đối với mỗi cấu trúc tinh thể, tồn tại một ô đơn vị quy ước, thường được chọn để mạng
tinh thể có tính đối xứng cao nhất. Tuy vậy, ô đơn vị quy ước không phải luôn luôn là lựa
chọn nhỏ nhất. Ô nguyên tố mới là một lựa chọn nhỏ nhất mà từ đó ta có thể tạo nên tinh
thể bằng cách lặp lại ô nguyên tố. Ô Wigner-Seitz là một loại ô nguyên tố mà có tính đối
xứng giống như của mạng tinh thể.
Hệ tinh thể
Hệ tinh thể là một nhóm điểm của các mạng tinh thể (tập hợp các phép đối xứng quay và
đối xứng phản xạ mà một điểm của mạng tinh thể không biến đối). Hệ tinh thể không có
các nguyên tử trong các ô đơn vị. Nó chỉ là những biểu diễn hình học mà thôi. Có tất cả
bảy hệ tinh thể. Hệ tinh thể đơn giản nhất và đối xứng cao nhất là hệ lập phương, các hệ
tinh thể khác có tính đối xứng thấp hơn là: hệ sáu phương, hệ bốn phương, hệ ba phương
(còn gọi là hình mặt thoi), hệ thoi, hệ một nghiêng, hệ ba nghiêng. Một số nhà tinh thể
học coi hệ tinh thể ba phương là một phần của hệ tinh thể sáu phương.
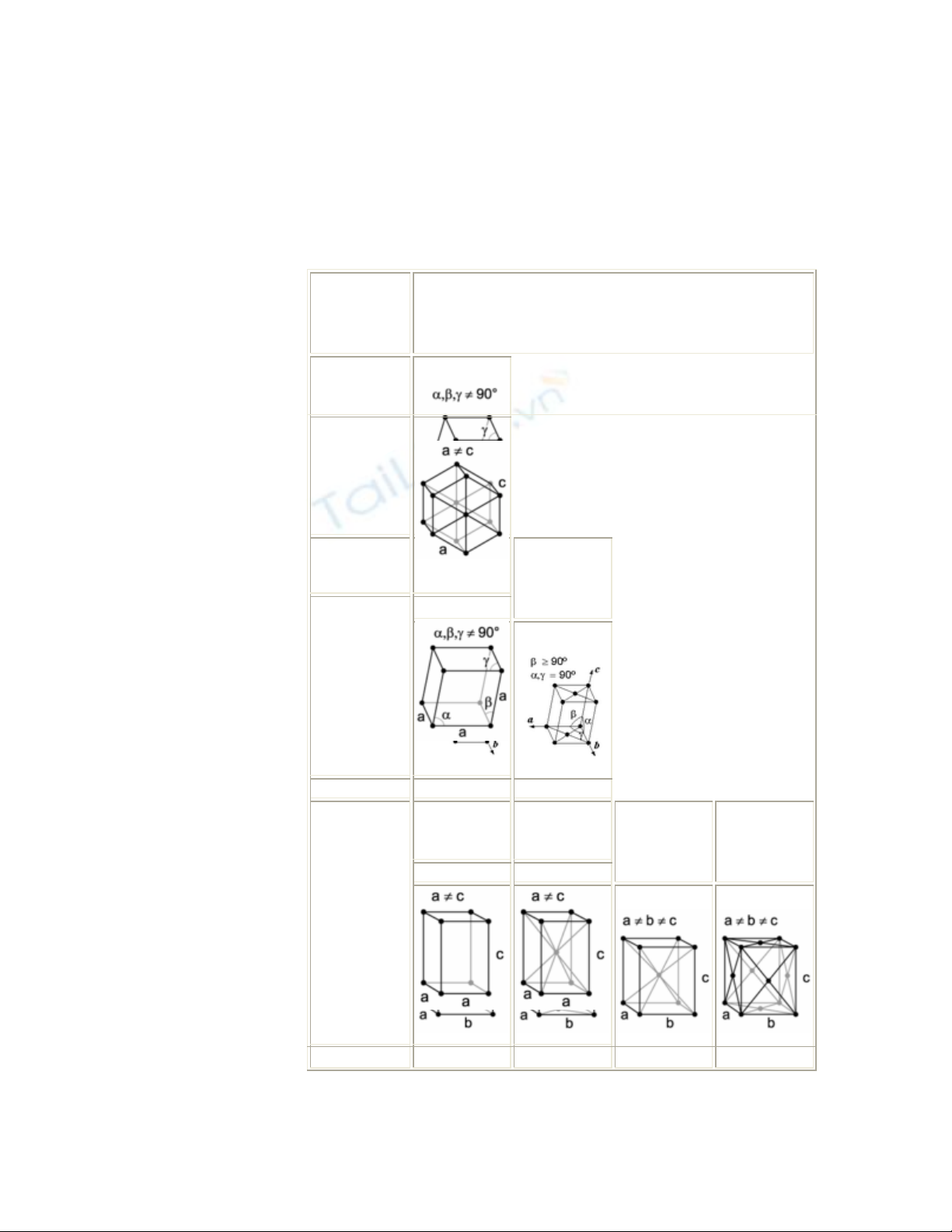
Phân loại
các loại
mạng tinh
thể
Hệ tinh thể Mạng tinh thể
Ba nghiêng
đơn giản tâm đáy
Một nghiêng
đơn giản tâm đáy tâm khối tâm mặt
Trực thoi
Sáu phương
Ba phương
đơn giản tâm khối
Bốn phương
Mạng Bravais là
một tập hợp các
điểm tạo thành từ
một điểm duy nhất
theo các bước rời
rác xác định bởi
các véc tơ cơ sở.
Trong không gian
ba chiều có tồn tại 14 mạng Bravais (phân biệt với nhau bởi các nhóm không gian). Tất
các các vật liệu có cấu trúc tinh thể đều thuộc vào một trong các mạng Bravais này
(không tính đến các giả tinh thể). 14 mạng tinh thể được phân theo các hệ tinh thể khác
nhau được trình bày ở phía bên phải của bảng.
đơn giản tâm khối tâm mặt
Lập phương
Cấu trúc tinh thể là một trong các mạng tinh thể với một ô đơn vị và các nguyên tử có
mặt tại các nút mạng của các ô đơn vị nói trên.
Nhóm điểm và nhóm không gian
Nhóm điểm tinh thể học hoặc lớp tinh thể là một tập hợp các phép đối xứng không tịnh
tiến mà dưới tác dụng của các phép đối xứng đó, tinh thể trở lại vị trí như cũ. Có tất cả 32
lớp tinh thể.
Nhóm không gian của một cấu trúc tinh thể được tạo thành từ các phép đối xứng tịnh tiến
bổ sung vào các phép đối xứng của các nhóm điểm. Có tất cả 230 nhóm không gian như
vậy.
Sai hỏng mạng
Các tinh thể thực thường có các sai hỏng mạng hoặc là các điểm bất thường có mặt trong
cấu trúc tinh thể lý tưởng nói ở trên. Các sai hỏng này có vai trò quyết định đến tính chất
cơ và điện của các tinh thể thực. Đặc biệt là bất định xứ trong tinh thể cho phép tinh thể
biến dạng dễ dàng hơn nhiều so với tinh thể hoàn hảo.