ĐI N H CỆ Ọ
A/ Các lo i m ch đi n:ạ ạ ệ
I/ Các ph ng pháp v l i m ch đi nươ ẽ ạ ạ ệ
1/ Tr i m ch đi nả ạ ệ
2/ Quy t c đi n thắ ệ ế
II/ M t s ph ng pháp gi i m ch đi n c b nộ ố ươ ả ạ ệ ơ ả
1/ Quy t c nút đi n thắ ệ ế
2/ Quy t c chia dòngắ
3/ Quy t c chia thắ ế
III/ Các lo i m ch đi n c b n:ạ ạ ệ ơ ả
1/ M ch c uạ ầ
a/ M ch gi c uạ ả ầ
b/ m ch c uạ ầ
c/ m ch liên c uạ ầ
2/ M ch vô h nạ ạ
3/ M ch tu n hoànạ ầ
4/ M ch đi x ngạ ố ứ
IV/Thi t k m ch đi n theo yêu c uế ế ạ ệ ầ
1/ Tìm s đi n tr thích h p cho 1 m ch đi nố ệ ở ợ ạ ệ
2/ M c m ch đi n có đi n tr t ng đng cho tr cắ ạ ệ ệ ở ươ ươ ướ
3/ M c m ch đi n cho các thi t b đi n ho t đng theo yêu c u cho tr cắ ạ ệ ế ị ệ ạ ộ ầ ướ
4/ m c m ch đi n đi x ng v i các đènắ ạ ệ ố ứ ớ
B/ M ch đi n có d ng c đo:ạ ệ ụ ụ
1/ Vai trò c a vôn k và ampe k trong m ch đi nủ ế ế ạ ệ
2/ M r ng thang đo cho vôn k và ampe kở ộ ế ế
3/ Cách m c các d ng c đo trong m ch đi nắ ụ ụ ạ ệ
C/ Bài toán v s bi n đi các đi l ng trong m ch đi n – giá tr l n nh t và nh nh tề ự ế ổ ạ ượ ạ ệ ị ớ ấ ỏ ấ
1/ Xét s bi n đng c a m t đi l ng trong m ch đi nự ế ộ ủ ộ ạ ượ ạ ệ
2/ Tìm min – max c a các đi l ng trong m t m ch đi nủ ạ ượ ộ ạ ệ
D/ Bài toán nhi t – đi n:ệ ệ
1/ Bài toán không có s trao đi nhi t v i bên ngoàiự ổ ệ ớ
2/ Bài toán có s trao đi nhi t v i bên ngoài.ự ổ ệ ớ
E/ Bài toán đ thồ ị
F/ Bài toán m ch đi n ch a ngu nạ ệ ứ ồ
1/ Ch a 1 ngu nứ ồ
2/ Ch a nhi u ngu n n i ti p, song songứ ề ồ ố ế
3/ Ch a ngu n xung điứ ồ ố
G/ Bài toán th c nghi mự ệ
H/ Bài toán h p đenộ
N I DUNG C THỘ Ụ Ể
A/ Các lo i m ch đi n:ạ ạ ệ
I/ Các ph ng pháp v l i m ch đi nươ ẽ ạ ạ ệ
1/ Tr i m ch đi nả ạ ệ
PP:
+ Nh ng đi m đc n i v i nhau b i nh ng đo n dây n i có đi n tr không đáng k đc ch p l i ữ ể ượ ố ớ ở ữ ạ ố ệ ở ể ượ ậ ạ
v i nhau. nh ng đo n m ch có đi n tr r t l n s đc b kh i m ch đi nớ ữ ạ ạ ệ ở ấ ớ ẽ ượ ỏ ỏ ạ ệ
+ Ghi nh ng đi m trên m ch đi n sau khi đã đc ch p ho c sau khi đã b nh ng đo n m ch theo ữ ể ạ ệ ượ ậ ặ ỏ ữ ạ ạ
nguyên t c: Nh ng đi m hai đu là ngu nắ ữ ể ầ ồ
+ D a vào m ch đi n sau khi đã bi n đi đ v l i m ch đi n. ự ạ ệ ế ổ ể ẽ ạ ạ ệ
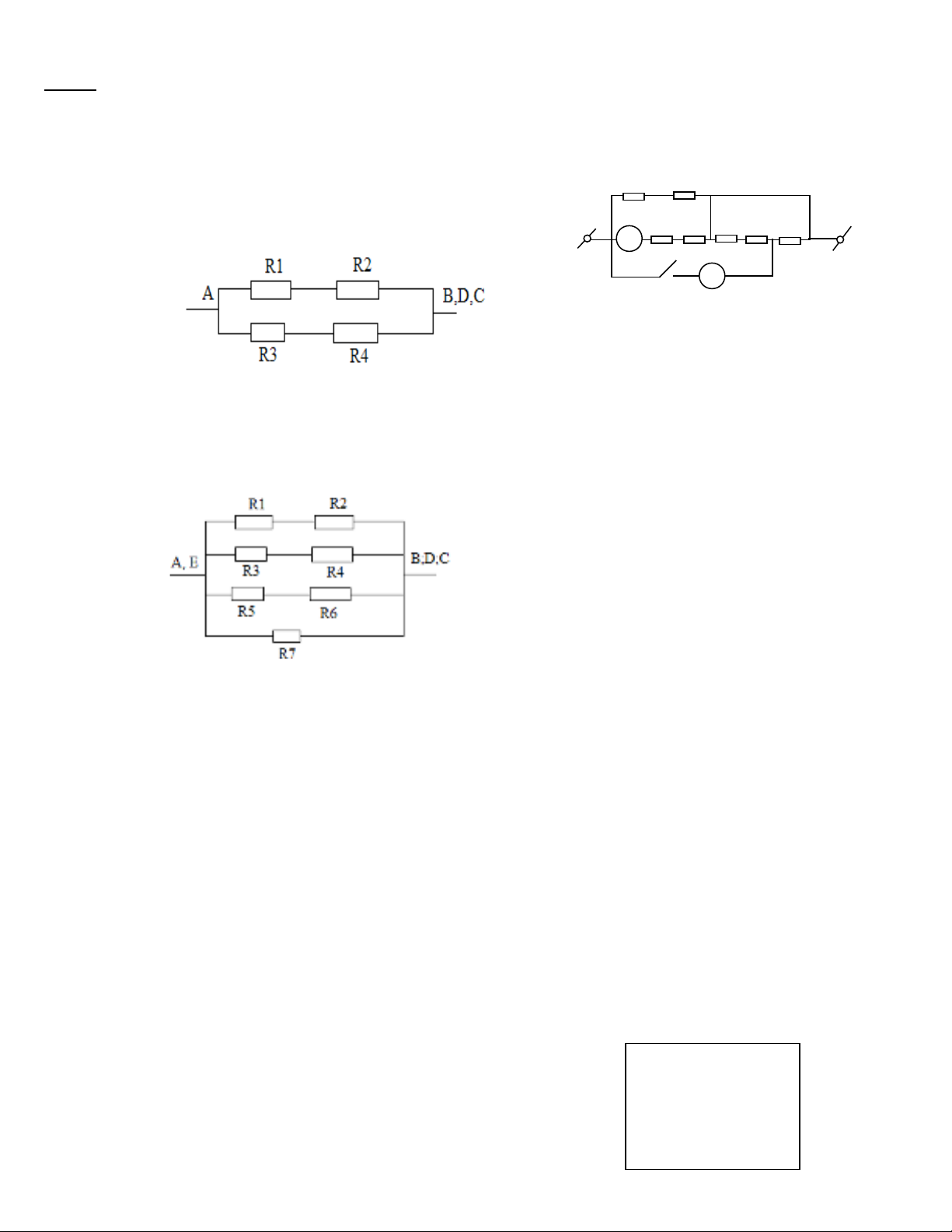
Bài 1: Cho m ch đi n nh hình v bên, các đi n tr Rạ ệ ư ẽ ệ ở 1 = R2 = R3 = R4 = R5 = R6 = R7 = 20.Đt gi a 2 đi m A,ặ ữ ể
B m t hi u đi n th không đi Uộ ệ ệ ế ổ AB = 40V, các ampe k Aế1, A2, khoá K và các dây n i có đi n tr không đángố ệ ở
k .Tính đi n tr c a đo n m ch AB và s ch c a các Ampe k trong 2 tr ng h p sau:ể ệ ở ủ ạ ạ ố ỉ ủ ế ườ ợ
a) Khoá K mở
b) Khoá K đóng
Gi i:ả
a/ Khi K m . Ch p các đi m B, D, C v i nhau. ở ậ ể ớ
M ch đi n đc v l i:ạ ệ ượ ẽ ạ
T đó d dàng tính đc đi n tr t ng đng c a m ch đi n.ừ ễ ượ ệ ở ươ ươ ủ ạ ệ
b/Khi K đóng: Ch p A và E, Ch p B, D và C. M ch đi n đc ậ ậ ạ ệ ượ
v l i nh sau:ẽ ạ ư
T đó d dàng tính đc đi n tr t ng đng c a m ch đi n.ừ ễ ượ ệ ở ươ ươ ủ ạ ệ
2/ Quy t c đi n thắ ệ ế
+ các m ch đi n có tính đi x ng, ngoài vi c ch p các nút có cùng đi n th ho c b các đi n tr trên Ở ạ ệ ố ứ ệ ậ ệ ế ặ ỏ ệ ở
các đo n m ch n i gi a hai đi m có cùng đi n th . Đôi khi ta ph i tách các nút đ bi n đi m ch đi n.ạ ạ ố ữ ể ệ ế ả ể ế ổ ạ ệ
Vi c tác các nút ph i đc th a mãn các yêu c u sau.ệ ả ượ ỏ ầ
a/ Ch tác các nút có t 4 đu n i dây tr lênỉ ừ ầ ố ở
b/ sau khi tách, các nút m i ph i có cùng đi n th .ớ ả ệ ế
+ Vi c xác đnh các nút có cùng đi n th ph thu c vào tính đi x ng c a t ng m ch đi n.ệ ị ệ ế ụ ộ ố ứ ủ ừ ạ ệ
Bài 1: tính đi n tr các m ch đi n sau:ệ ở ạ ệ
a/ cho m ch đi n nh hình v : ạ ệ ư ẽ
Các đo n dây n i có đi n tr nh nhau và có giá tr b ng r.ạ ố ệ ở ư ị ằ
xác đnh đi n tr :ị ệ ở
RAC; RAC’ ; RAB.
A
R1R2
R3R5
R4
K
B
R6R7
A1
C
D
E
A2
B
A
C
D
A’
D’ C’
B’
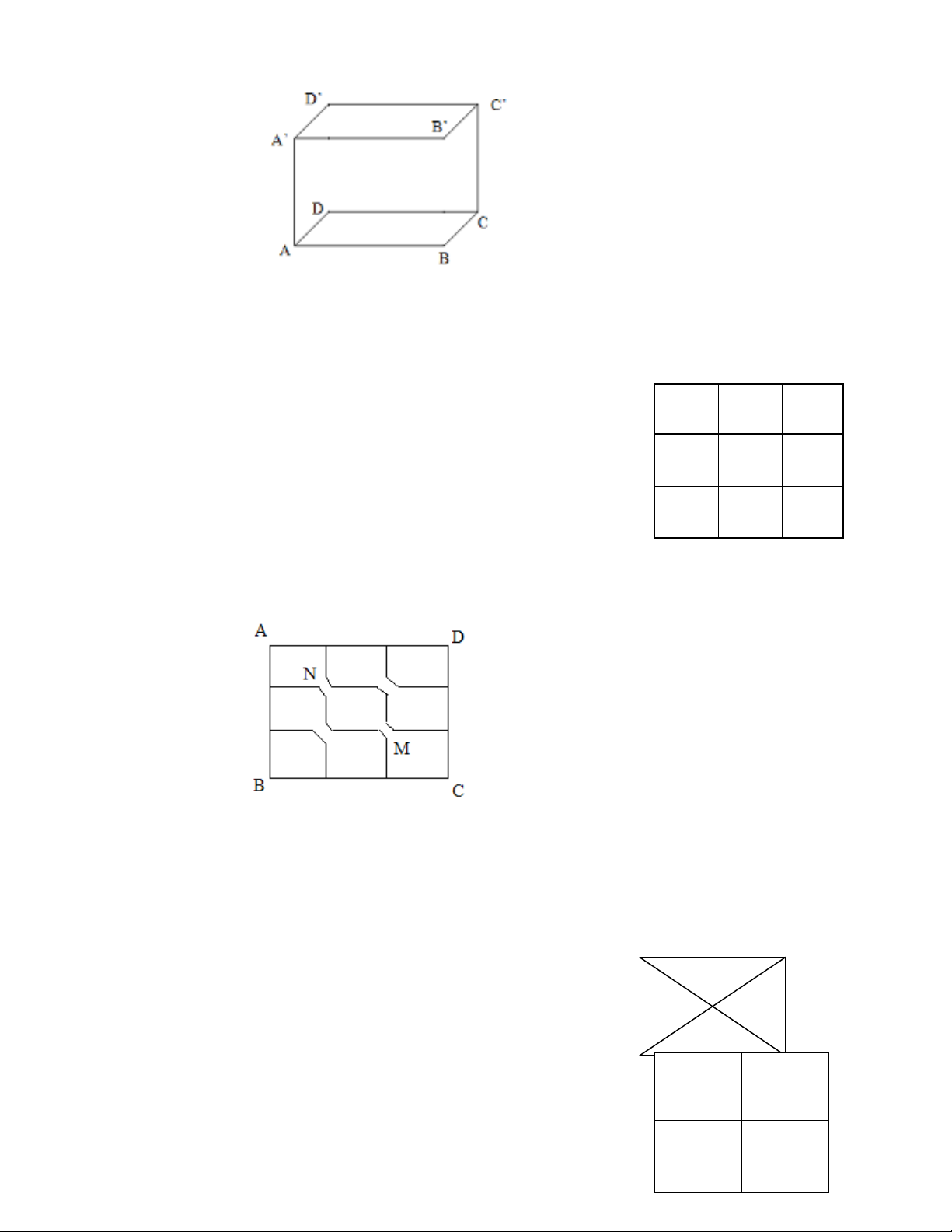
HD: Vì B, B’ có cùng đi n th . D, D’ có cùng đi n th . Nên ta có th b đo n BB’ và CC’ ra kh i m ch đi n. ệ ế ệ ế ể ỏ ạ ỏ ạ ệ
M ch đi n m i: ạ ệ ớ
Dùng ph ng pháp tr i m ch đi n, d dàng tính đc đi n tr t ng đng c a m ch đi nươ ả ạ ệ ễ ượ ệ ở ươ ươ ủ ạ ệ
b/ Cho m ch đi n nh hình v . Các đo n dây n i có đi n tr nh nhau và cóạ ệ ư ẽ ạ ố ệ ở ư
giá tr b ng r. Xác đinh đi n tr :ị ằ ệ ở
RAC; RMN
HD: Th c hi n tách các nút thành các nút m i có cùng đi n th . ta đc m ch đi n m iự ệ ớ ệ ế ượ ạ ệ ớ
Dùng ph ng pháp tr i m ch đi n. d dàng tính đc đi n tr t ng đng c a m ch đi nươ ả ạ ệ ễ ượ ệ ở ươ ươ ủ ạ ệ
b/ Cho m ch đi n nh hình v . Các đo n dây n i có đi n tr nh nhau. ạ ệ ư ẽ ạ ố ệ ở ư
và có giá tr b ng r. Xác đnh đi n tr :ị ằ ị ệ ở
RAC; RAB; RAO
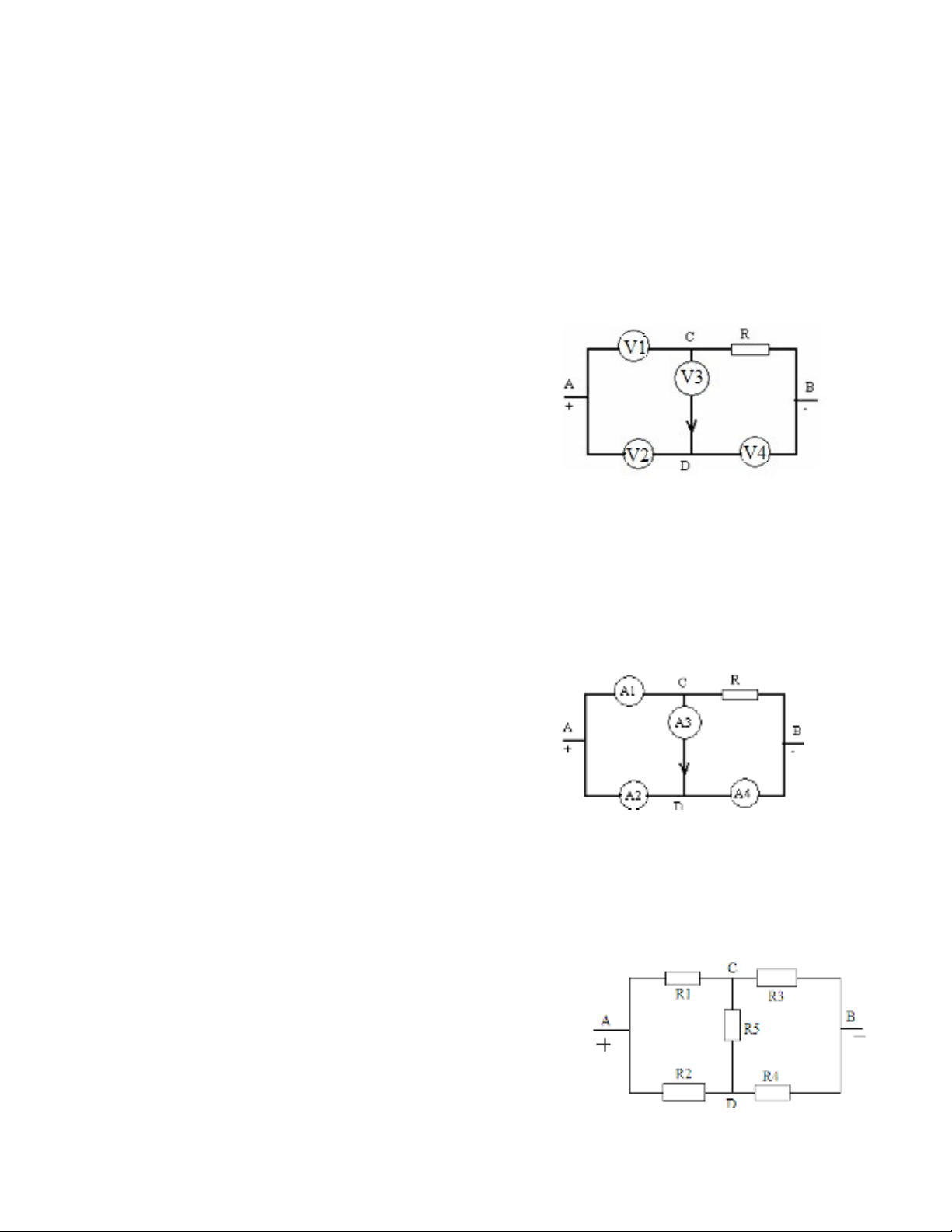
c/ Cho m ch đi n nh hình v . Các đo n dây n i có đi n tr nh nhauạ ệ ư ẽ ạ ố ệ ở ư
và có giá tr b ng r. xác đnh đi n tr :ị ằ ị ệ ở
RAC; RAB; RAO ; RMN.
AD
CB
O
A
B
D
C
O
M
N
P
Q
A
B
D
C
N
M
II/ M t s ph ng pháp gi i m ch đi n c b nộ ố ươ ả ạ ệ ơ ả
1/ Quy t c nút đi n thắ ệ ế
2/ Quy t c chia dòng và quy t c chia th :ắ ắ ế
+ T ng các dòng đi n đi vào 1 nút b ng t ng các dòng đi n đi ra t nút y:ổ ệ ằ ổ ệ ừ ấ
+ T ng đ gi m hi u đi n th trên m t đo n m ch kín b ng 0ổ ộ ả ệ ệ ế ộ ạ ạ ằ
Bài 1: Cho m ch đi n nh hình v . Các vôn k gi ng nhau.ạ ệ ư ẽ ế ố
S ch các vôn k V2 và V4 l n l t là 1V và 3V. ố ỉ ế ầ ượ
Dòng đi n qua đi n tr R có c ng đ là 1A. ệ ệ ở ườ ộ
Xác đnh s ch V1, V2 và giá tr đi n tr Rị ố ỉ ị ệ ở
HD: T i nút D ta có: Iạ4 = I3 + I2. Nhân 2 v v i Rế ớ v ta đc: ượ
Rv I4 = Rv I3 + Rv I2 hay: U4 = U3 + U2 t đó ta có: Uừ3 = U4 – U2 = 2V
L i có: Uạ1 = U3 – U2 = 1V.
UR = U3 + U4 = 5V nên R = 5
Ω
Bài 2: Cho m ch đi n nh hình v :ạ ệ ư ẽ
Các ampe k gi ng nhau. Aế ố 1 ch 3A; Aỉ2 ch 4Aỉ
1/ Xác đnh s ch Aị ố ỉ 3; A4; IR
2/ Bi t RếA = kR; Tính k.
HD: 1/ Có: U2 = U1 + U3
RAI2 = RAI1 + RAI3
I2 = I1 + I3 t nên Iừ3 = I2 – I1 = 1A
L i có: Iạ4 = I2 + I3 = 5A
2/ Có: IR = I1 – I3
IR = 2A
Mà: U3 + U4 = UR
kR + 5kR = 2R
K = 1/3
III/ Các lo i m ch đi n c b n:ạ ạ ệ ơ ả
1/ M ch c uạ ầ
A/ Các ph ng trình c b n c a m ch c u:ươ ơ ả ủ ạ ầ
Xét m ch c u nh hình v :ạ ầ ư ẽ
Các ph ng trình sau đc g i là ph ng trình c b n:ươ ượ ọ ươ ơ ả
+ Ph ng trình nút t i C, Dươ ạ
+ UAC + UCB = UAD + UDB
+ UAC + UCD + UDB = UAD + UDC + UCB
+ Ph ng trình t i các m t ACD và BCDươ ạ ắ
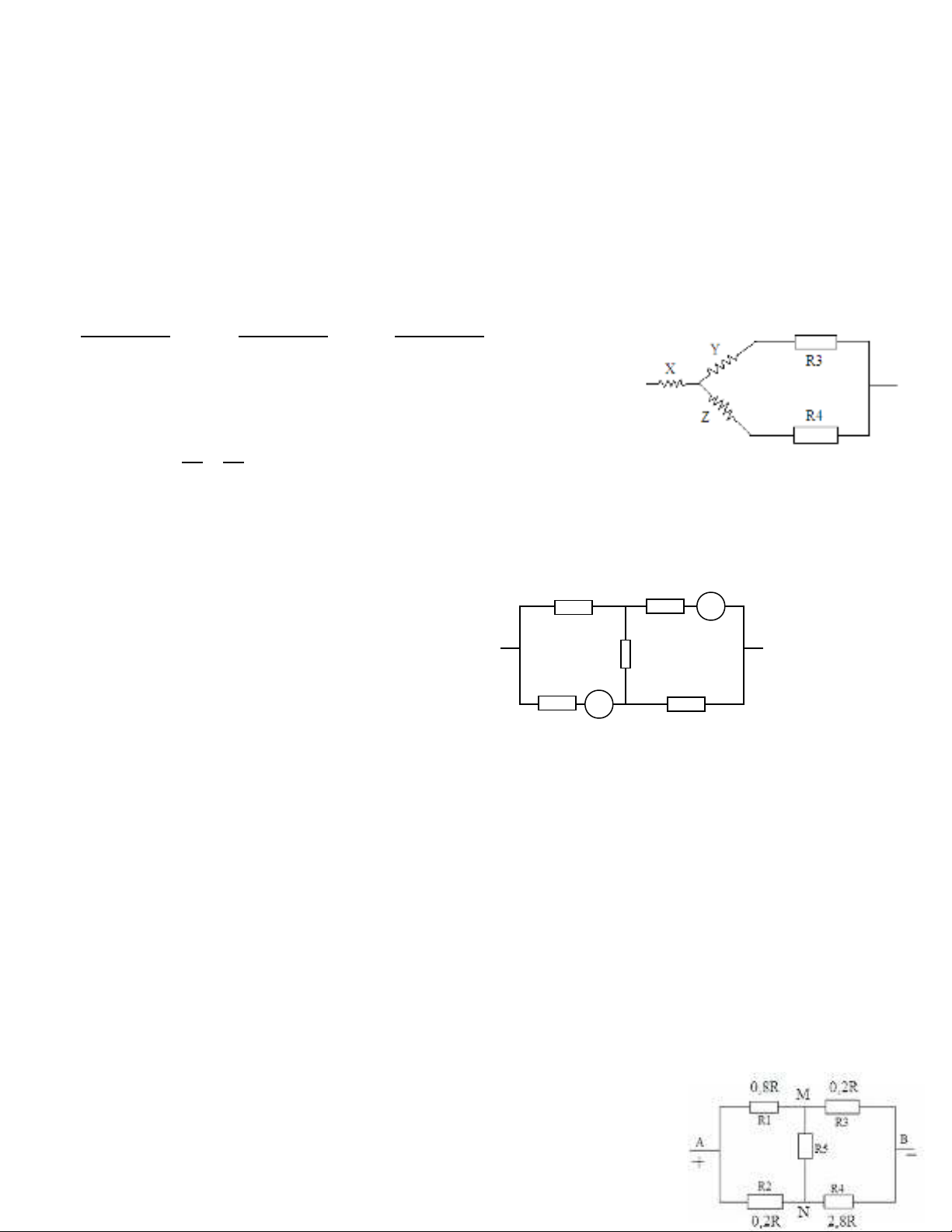
B/ Ph ng pháp chuy n m ch: ươ ể ạ
Thông th ng s d ng ph ng pháp chuy n m ch tam giác thành m ch sao đ tính đi n tr t ng ườ ử ụ ươ ể ạ ạ ể ệ ở ươ
đng:ươ
X =
1 2
1 2 5
R R
R R R+ +
Y =
1 5
1 2 5
R R
R R R+ +
Z =
2 5
1 2 5
R R
R R R+ +
T đó tính đc đi n tr đo n m ch.ừ ượ ệ ở ạ ạ
Chú ý: S d ng ph ng trình nút t i C, D cũng tính đc đi n tr c a nó.ử ụ ươ ạ ượ ệ ở ủ
C/ M ch c u có ạ ầ
3
1
2 4
R
R
R R
=
thì không có dòng đi n qua Rệ5. Khi đó m ch đc g i là m ch c u cân b ngạ ượ ọ ạ ầ ằ
Bài toán 1: Cho m ch đi n nh hình v :ạ ệ ư ẽ
R1 = 3R; R2 = R3 = R4 = R5 = R
Bi t ampe k Aế ế 1 ch Iỉ1.
H i ampe k Aỏ ế 2 ch bao nhiêu?ỉ
B qua đi n tr c a ampe k và các dây n i.ỏ ệ ở ủ ế ố
Gi i:ả Xét t i nút A và B ta có: Iạ1+I3 = I2 +I4 (1)
M t khác: UặAB = (I3+I2)R = (3I1 +I4)R I3 +I2 = 3I1 + I4 (2)
T (1) và (2) ta đc: Iừ ượ 2 = 2I1
V y s ch c a ampe k Aậ ố ỉ ủ ế 2 là 2I1
Bài toán 2: t m t cu n dây đng ch t ti t di n đu, làm b ng h p kim có đi n tr su t l n, ng i ta c t ra ừ ộ ộ ồ ấ ế ệ ề ằ ợ ệ ở ấ ớ ườ ắ
hai đo n dây dài lạ1 = 1 m và l2 = 3 m. r i m c chúng song song v i nhau vào m t ngu n đi n. G i hai đi m nút ồ ắ ớ ộ ồ ệ ọ ể
là A, B. ng i ta đánh d u đi m M trên dây th nh t mà MB=0,2 m. và đi m N trên dây th hai mà AN = 0,2 m.ườ ấ ể ứ ấ ể ứ
r i n i M, N b ng m t đo n dây th 3 có chi u dài lồ ố ằ ộ ạ ứ ề x đc c t ra t cu n dây trên.ượ ắ ừ ộ
Tính t s c ng đ dòng đi n trong hai đo n dây AM và NB.ỷ ố ườ ộ ệ ạ
HD: M ch đi n g m các dây d n sau khi n i thì tr thành m t m ch c u. Kí hi u các đo n dây đi nạ ệ ồ ẫ ố ở ộ ạ ầ ệ ạ ệ
tr nh hình v .ở ư ẽ
G i đi n tr c a 0,1 m chi u dài dây d n là R. thì giá tr đi n tr c a các đo n dây nh hình v :ọ ệ ở ủ ề ẫ ị ệ ở ủ ạ ư ẽ
Ta có: U1 + U3 = U2 + U4
0,8I1 + 0,2I3 = 0,2I2 + 2,8I4
4I1 + I3 = I2 + 14I4 (1)
M t khác, ta cũng có: Iặ1 + I2 = I3 + I4 (2)
A1
A2
R3R2
R1
R5
R4
A
+
B
_