Fly Education Thầy Hải Toán
K/82/10/22 Nguyễn Văn Linh – Hải Châu – Đà Nẵng
SĐT: 0905958921
PHƯƠNG TRÌNH
LƯ
Ợ
NG GIÁC
TÀI LIỆU LƯU HÀNH NỘI BỘ
2021
Nơi Đâu Có Ý Chí Ở Đó Có Con Đường
MỤC LỤC
Chương1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 1
§0 – Công thức lượng giác cần nhớ 1
§1 – HÀM SỐ LƯỢNG GIÁC 3
AA KIẾN THỨC CẦN NHỚ...........................................................................................................................3
BB PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN.......................................................................................4
|Dạng 1. Tìm tập xác định của hàm số lượng giác......................................................................4
|Dạng 2. Tính chẵn lẻ của hàm số...................................................................................................7
|Dạng 3. Tìm giá trị lớn nhất - giá trị nhỏ nhất ..........................................................................8
CC BÀI TẬP TRẮC NGHIỆM.....................................................................................................................13
§2 – PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN 17
AA KIẾN THỨC CẦN NHỚ........................................................................................................................17
BB PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN....................................................................................19
|Dạng 1. Giải các phương trình lượng giác cơ bản....................................................................19
|Dạng 2. Giải các phương trình lượng giác dạng mở rộng.......................................................21
|Dạng 3. Giải các phương trình lượng giác có điều kiện xác định..........................................22
|Dạng 4. Giải các phương trình lượng giác trên khoảng (a;b)cho trước............................24
CC BÀI TẬP TRẮC NGHIỆM.....................................................................................................................26
§3 – MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP 29
AA KIẾN THỨC CẦN NHỚ........................................................................................................................29
BB PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN....................................................................................30
|Dạng 1. Giải phương trình bậc nhất đối với một hàm số lượng giác...................................30
|Dạng 2. Giải phương trình bậc hai đối với một hàm số lượng giác .....................................33
|Dạng 3. Giải phương trình bậc nhất đối với sinx và cosx.......................................................37
|Dạng 4. Phương trình đẳng cấp bậc hai đối với sinx và cosx................................................41
|Dạng 5. Phương trình chứa sin x±cos xvà sin x·cos x...........................................................43
CC BÀI TẬP TRẮC NGHIỆM.....................................................................................................................45
§4 – MỘT SỐ PHƯƠNG PHÁP GIẢI PT LƯỢNG GIÁC 48
AA PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN....................................................................................48
|Dạng 1. Biến đổi đưa phương trình về dạng phương trình bậc hai (ba) đối với một hàm
số lượng giác.............................................................................................................................................48
|Dạng 2. Biến đổi asinx + bcosx....................................................................................................49
/63 i/63 pTh.S Phạm Hùng Hải – Ô0905.958.921
Gv Ths: Phạm Hùng Hải
MỤC LỤC Gv Chuyên Toán 10 - 11 - 12 & LTĐH
ii
|Dạng 3. Biến đổi đưa về phương trình tích................................................................................50
|Dạng 4. Một số bài toán biện luận theo tham số.....................................................................51
BB BÀI TẬP TỰ LUYỆN.............................................................................................................................55
§5 – ĐỀ ÔN TẬP CUỐI CHƯƠNG 57
AA Đề số 1.......................................................................................................................................................57
BB Đề số 2.......................................................................................................................................................60
§6 – ĐÁP ÁN TRẮC NGHIỆM CÁC CHỦ ĐỀ 63
/63 ii/63 pTh.S Phạm Hùng Hải – Ô0905.958.921
Nơi Đâu Có Ý Chí Ở Đó Có Con Đường
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
1
C
h
ư
ơ
n
g
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
BÀI 0. CÔNG THỨC LƯỢNG GIÁC CẦN NHỚ
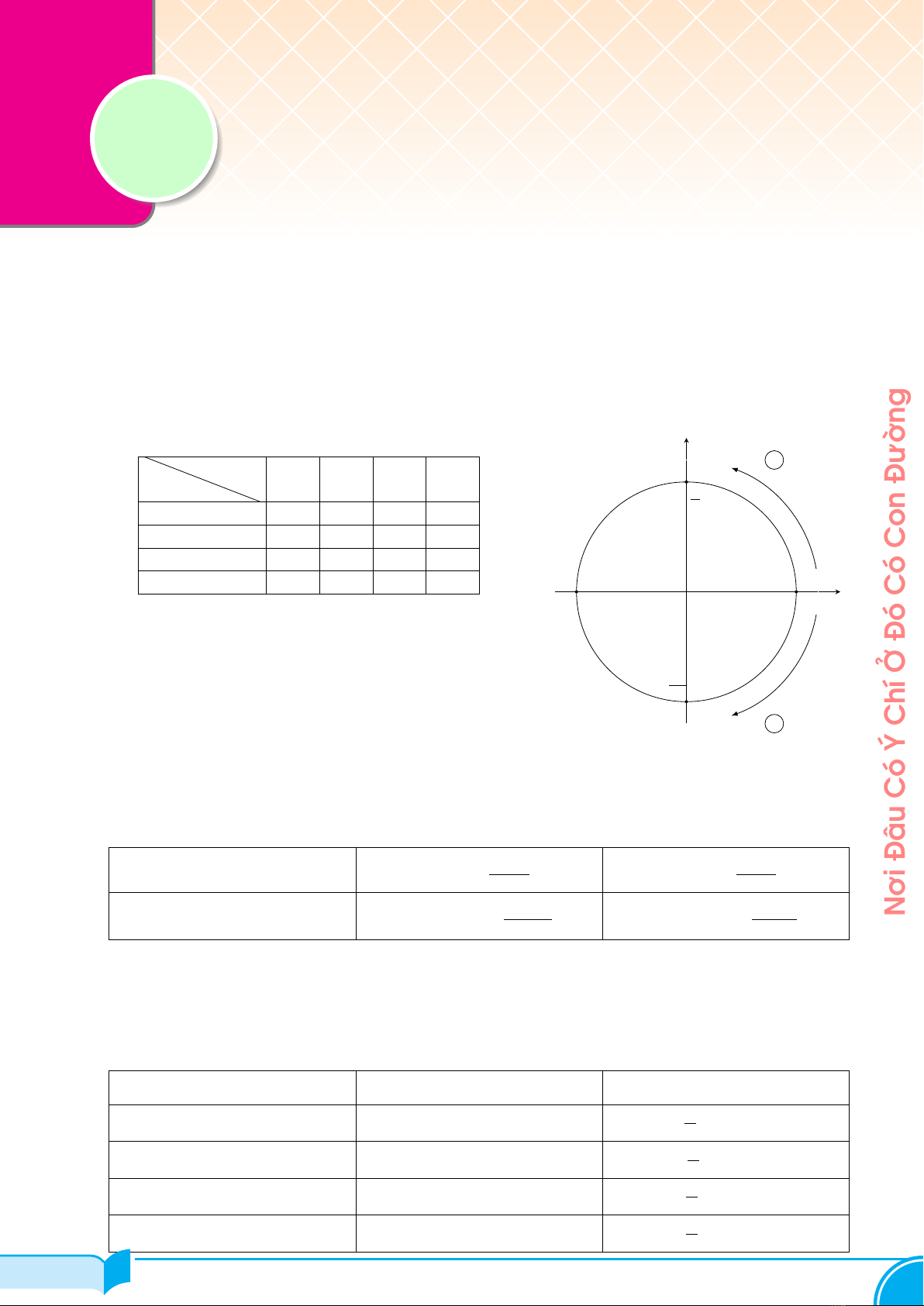
1) Đường tròn lượng giác và dấu của các giá trị lượng giác
GTLG Góc (I) (II) (III) (IV )
sin α++− −
cos α+− − +
tan α+−+−
cot α+−+−
(Nhất cả - Nhị sin - Tam tan - Tứ cos)x
cos x
y
sin x
O1
−1
1
−1
(I)(II)
(III) (IV )
2π
0
π
2
3π
2
π
+
−
2) Công thức lượng giác cơ bản
sin2α+cos2α=1 tan α=sin α
cos αcot α=cos α
sin α
tan α·cot α=1 1 +tan2α=1
cos2α1+cot2α=1
sin2α
3) Cung góc liên kết
Cung (góc) đối nhau Cung (góc) bù nhau Cung (góc) phụ nhau
cos(−α) = cos αsin(π−α) = sin αsin π
2−α=cos α
sin(−α) = −sin αcos(π−α) = −cos αcos π
2−α=sin α
tan(−α) = −tan αtan(π−α) = −tan αtan π
2−α=cot α
cot(−α) = −cot αcot(π−α) = −cot αcot π
2−α=tan α
/63 1/63 pTh.S Phạm Hùng Hải – Ô0905.958.921
Gv Ths: Phạm Hùng Hải
0. Công thức lượng giác cần nhớ Gv Chuyên Toán 10 - 11 - 12 & LTĐH
2
Cung (góc) hơn kém πCung (góc) hơn kém π
2
cos(π+α) = −cos αsin π
2+α=cos α
sin(π+α) = −sin αcos π
2+α=−sin α
tan(π+α) = tan αtan π
2+α=−cot α
cot(π+α) = cot αcot π
2+α=−tan α
4) Công thức cộng
sin (a±b) = sin a·cos b±cos a·sin bcos (a±b) = cos a·cos b∓sin a·sin b
tan (a+b) = tan a+tan b
1−tan a·tan btan (a−b) = tan a−tan b
1+tan a·tan b
Hệ quả: tan π
4+x=1+tan x
1−tan xvà tan π
4−x=1−tan x
1+tan x
5) Công thức nhân đôi - hạ bậc - nhân ba
Nhân đôi Hạ bậc Nhân ba
sin 2α=2 sin α·cos αsin2α=1−cos 2α
2sin 3α=3 sin α−4 sin3α
cos 2α=cos2α−sin2α
=2 cos2α−1
=1−2 sin2α
cos2α=1+cos 2α
2cos 3α=4 cos3α−3 cos α
tan 2α=2 tan α
1−tan2αtan2α=1−cos 2α
1+cos 2αtan 3α=3 tan α−tan3α
1−3 tan2α
cot 2α=cot2α−1
2 cot αcot2α=1+cos 2α
1−cos 2α
6) Công thức biến đổi tổng thành tích
cos a+cos b=2 cos a+b
2·cos a−b
2cos a−cos b=−2 sin a+b
2·sin a−b
2
sin a+sin b=2 sin a+b
2·cos a−b
2sin a−sin b=2 cos a+b
2·sin a−b
2
tan a+tan b=sin(a+b)
cos a·cos btan a−tan b=sin(a−b)
cos a·cos b
cot a+cot b=sin(a+b)
sin a·sin bcot a−cot b=sin(b−a)
sin a·sin b
Đặc biệt
sin x+cos x=√2 sin x+π
4
=√2 cos x−π
4
sin x−cos x=√2 sin x−π
4
=−√2 cos x+π
4
7) Công thức biến tích thành tổng
cos a·cos b=1
2[cos(a−b) + cos(a+b)] sin a·sin b=1
2[cos(a−b)−cos(a+b)]
sin a·cos b=1
2[sin(a−b) + sin(a+b)]
/63 2/63 pTh.S Phạm Hùng Hải – Ô0905.958.921