MỤC LỤC
MỤC LỤC
CHƯƠNG 1 HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 1
1. HÀMSỐLƯỢNGGIÁC........................................................ 1
A KIẾNTHỨCCẦNNHỚ............................................... 1
B PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN ..... ... ... ...... ...... ..... 2
Dạng 1. Tìm tập xác định của hàm số lượng giác....................... 2
Dạng 2. Tính chẵn lẻ của hàm số...................................... 3
Dạng 3. Tìm giá trị lớn nhất - giá trị nhỏ nhất ......................... 4
C BÀITẬPTRẮCNGHIỆM............................................. 4
2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN.. ... ... ...... ...... ................... 8
A KIẾNTHỨCCẦNNHỚ............................................... 8
B PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN .. ... ... ... ...... ...... ..... 10
Dạng 1. Giải các phương trình lượng giác cơ bản ....................... 10
Dạng 2. Giải các phương trình lượng giác dạng mở rộng ................ 11
Dạng 3. Giải các phương trình lượng giác có điều kiện xác định.......... 11
Dạng 4. Giải các phương trình lượng giác trên khoảng (a;b)cho trước... 11
C BÀITẬPTRẮCNGHIỆM............................................. 12
3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP.. ... ... ... ...... ...... 15
A KIẾNTHỨCCẦNNHỚ............................................... 15
B PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN .. ... ... ... ...... ...... ..... 16
Dạng 1. Giải phương trình bậc nhất đối với một hàm số lượng giác .. ... . 16
Dạng 2. Giải phương trình bậc hai đối với một hàm số lượng giác........ 17
Dạng 3. Giải phương trình bậc nhất đối với sinx và cosx................. 17
Dạng 4. Phương trình đẳng cấp bậc hai đối với sinx và cosx............. 18
Dạng 5. Phương trình chứa sin x±cos xvà sin x·cos x................... 19
C BÀITẬPTRẮCNGHIỆM............................................. 20
4. MỘT SỐ PHƯƠNG PHÁP GIẢI PT LƯỢNG GIÁC .. ... ... ...... ...... .......... 23
A PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN .. ... ... ... ... ... ... ... ... .. 23
Dạng 1. Biến đổi đưa phương trình về dạng phương trình bậc hai (ba) đối
với một hàm số lượng giác ............................................ 23
Dạng 2. Biến đổi asinx + bcosx ....................................... 24
Dạng 3. Biến đổi đưa về phương trình tích ............................. 24
Dạng 4. Một số bài toán biện luận theo tham số ....................... 25
B BÀITẬPTỰLUYỆN................................................. 26
5. ĐỀÔNTẬPCUỐICHƯƠNG................................................... 28
A Đềsố1.............................................................. 28
B Đềsố2.............................................................. 31
6. ĐÁP ÁN TRẮC NGHIỆM CÁC CHỦ ĐỀ .. ... ... ... ... ... ... ...... ...... ........ 34
Trang i
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
CHƯƠNG
1HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG
TRÌNH LƯỢNG GIÁC
§1. HÀM SỐ LƯỢNG GIÁC
AA KIẾN THỨC CẦN NHỚ
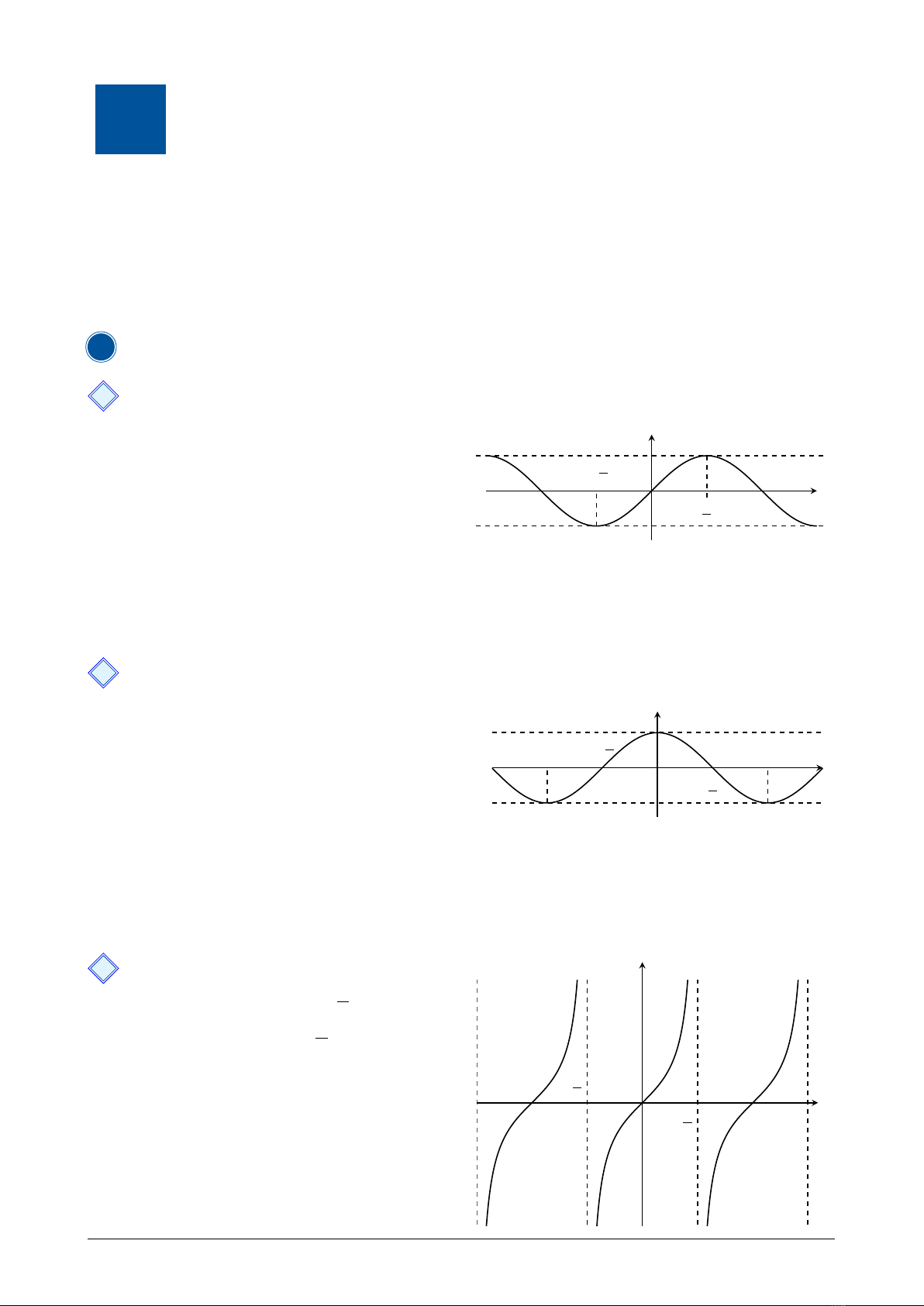
11 Hàm số y=sin x
•Tập xác định: D=R.
•Tập giác trị: [−1; 1], tức là −1≤sin x≤1,
∀x∈R.
•Hàm số y=sin xlà hàm số lẻ nên đồ thị hàm
số nhận gốc tọa độ Olàm tâm đối xứng.
•Hàm số y=sin xtuần hoàn với chu kì T=
2π, nghĩa là sin(x+k2π) = sin x, với k∈Z.
x
Đồ thị hàm số y=sin x
y
−ππ
−π
2
π
2
22 Hàm số y=cos x
•Tập xác định: D=R.
•Tập giác trị: [−1; 1], tức là −1≤cos x≤1,
∀x∈R.
•Hàm số y=cos xlà hàm số chẵn nên đồ thị
hàm số nhận trục Oy làm trục đối xứng.
•Hàm số y=cos xlà hàm số tuần hoàn với chu
kì T=2π, nghĩa là cos(x+k2π) = cos x, với
k∈Z.
x
Đồ thị hàm số y=cos x
y
−ππ
−π
2
π
2
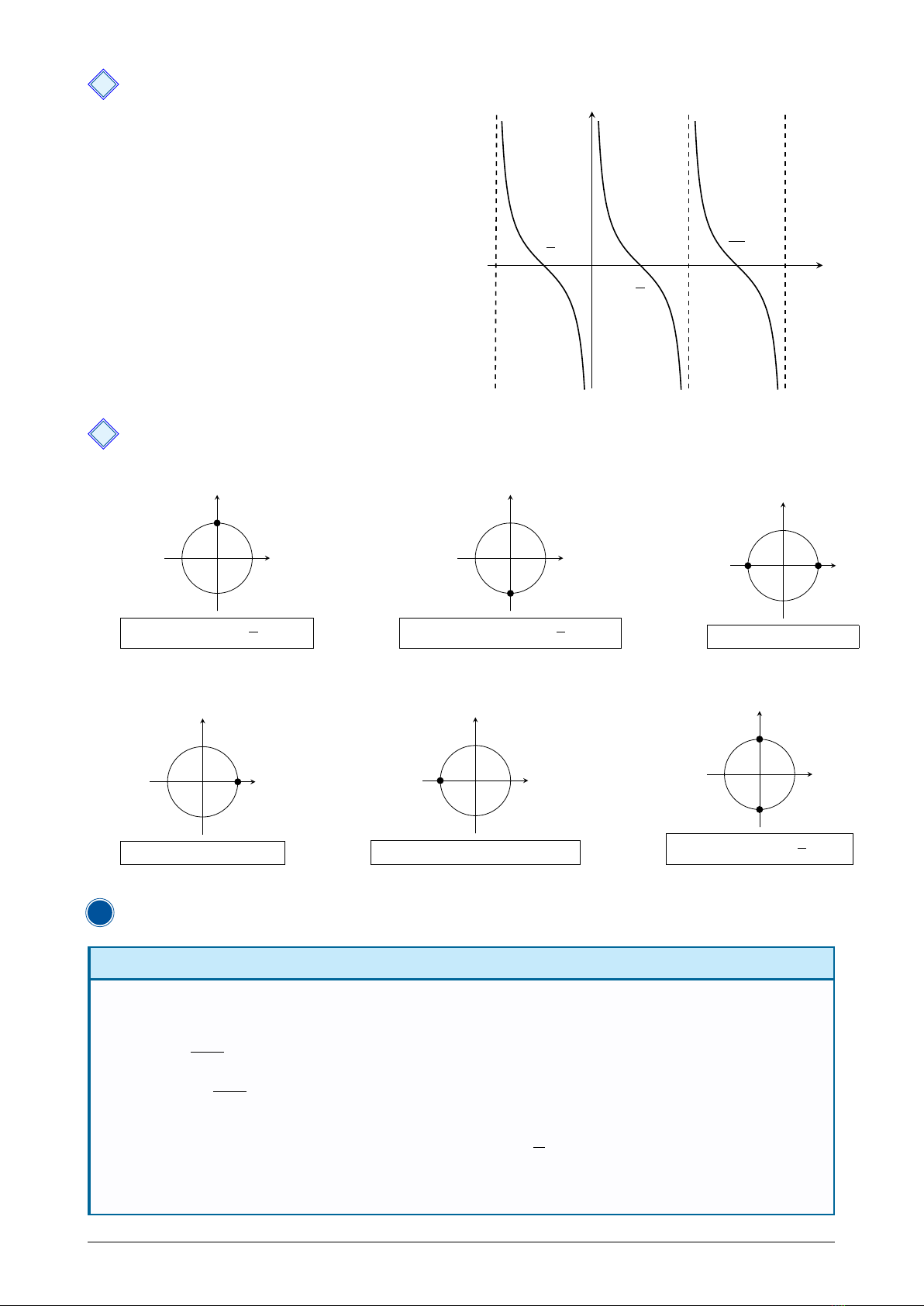
33 Hàm số y=tan x
•Điều kiện cos x6=0⇔x6=π
2+kπ,k∈Z.
Tập xác định: D=R\nπ
2+kπ,k∈Zo.
•Tập giá trị: R.
•Là hàm số lẻ.
•Là hàm số tuần hoàn với chu kì T=π, nghĩa
là tan(x+kπ) = tan x, với k∈Z.
x
y
O
−π
π
−π
2
π
2
Trang 1
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
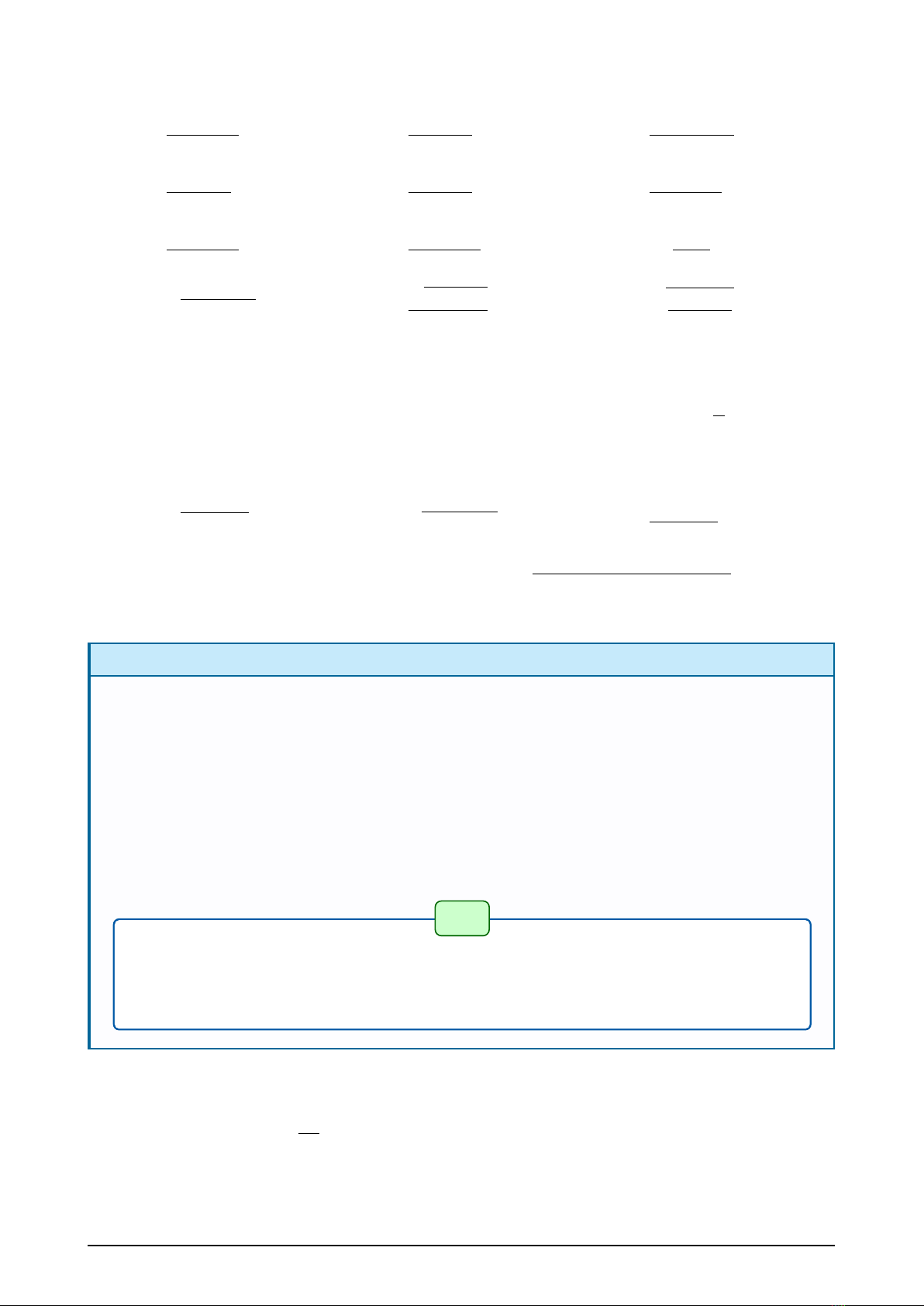
44 Hàm số y=cot x
•Điều kiện sin x6=0⇔x6=kπ,k∈Z.
Tập xác định: D=R\{kπ,k∈Z}.
•Tập giá trị: R.
•Là hàm số lẻ.
•Là hàm số tuần hoàn với chu kì T=π,
nghĩa là cot(x+kπ) = cot x, với k∈Z.x
y
O
−π
π
−π
2
π
2
3π
2
55 Một số trường hợp đặc biệt
Các trường hợp đặc biệt cho hàm y=sin x
cos
sin
O
B
sin x=1⇔x=π
2+k2π
cos
sin
O
B′
sin x=−1⇔x=−π
2+k2π
cos
sin
O
AA′
sin x=0⇔x=kπ
Các trường hợp đặc biệt cho hàm y=cos x
cos
sin
O
A
cos x=1⇔x=k2π
cos
sin
O
A′
cos x=−1⇔x=π+k2π
cos
sin
O
B
B′
cos x=0⇔x=π
2+kπ
BB PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
{DẠNG 1. Tìm tập xác định của hàm số lượng giác
Phương pháp giải. Ta chú ý một số điều kiện sau:
1. y=f(x)
g(x)xác định ⇔g(x)6=0.
2. y=2n
pf(x)xác định ⇔f(x)>0, trong đó n∈N∗.
3. y=tan [u(x)] xác định ⇔u(x)xác định và u(x)6=π
2+kπ,k∈Z.
4. y=cot [u(x)] xác định ⇔u(x)xác định và u(x)6=kπ,k∈Z.
Trang 2
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
#Ví dụ 1. Tìm tập xác định của các hàm số sau đây:
y=2 sin x+3
cos x
a) y=1+cos x
1−cos x
b) y=2+3 cos 2x
sin x
c)
y=1+cos x
1+sin x
d) y=sin x−3
cos x+1
e) y=2 sin x+3
cos x+2
f)
y=2 sin x+3
sin x−1
g) y=2 sin x−3
2 sin x+3
h) y=sin x−1
x+2.i)
y=√3−2 cos x.j) y=√cos x−2
1+cos x
k) y=…1+cos x
1−cos x
l)
#Ví dụ 2. Tìm tập xác định của các hàm số sau đây:
y=2 tan x+3a) y=2 tan 2x−4 sin xb) y=cot x+π
4+1c)
#Ví dụ 3. Tìm tất cả các giá trị của mđể hàm số sau có tập xác định R.
y=√m−cos xa) y=√2 sin x−mb) y=sin x−1
cos x+m
c)
#Ví dụ 4. Tìm tất cả các giá trị của mđể hàm số y=pcos2x−(2+m)cos x+2mcó tập xác
định R.
{DẠNG 2. Tính chẵn lẻ của hàm số
Phương pháp giải. Ta thực hiện các bước sau:
1. Tìm tập xác định Dcủa hàm số – Tập Dphải đối xứng.
2. Tính f(−x)(chỗ nào có biến x, ta thay bởi −x) và thu gọn kết quả. Khi đó
•Nếu f(−x) = f(x): hàm số đã cho là hàm chẵn.
•Nếu f(−x) = −f(x): hàm số đã cho là hàm lẻ.
•Nếu không rơi vào 2 trường hợp trên, ta kết luận hàm số không chẵn, không lẻ.
CHÚ Ý
Hàm số y=sin xlà hàm số lẻ.①Hàm số y=cos xlà hàm số chẵn.②
Hàm số y=tan xlà hàm số lẻ.③Hàm số y=cot xlà hàm số lẻ.④
#Ví dụ 5. Xét tinh chẵn lẻ của hàm số
y=f(x) = sin Å2x+9π
2ã;a) y=f(x) = tan x+cot x.b)
#Ví dụ 6. Xét tính chẵn lẻ của hàm số y=tan72x·sin 5x.
Trang 3