ThS. Lê 
07/2013
Chuyên 
M – Logarit
–
E m a i l : v a n d o a n _ a u t o m o b i l e @ y a h o o . c o m . v n
MC LC
Trang
A – Công thc m & logarit cn nh .................................................................................... 1
B – Phương trình & Bt phương trình m ........................................................................... 3
Dng toán 1. Gii bng cách a v cùng c! s" ho#c logarit hóa ..................................... 3
Các thí d$ ................................................................................................... 3
Bài t%p t!ng t& ......................................................................................... 16
Dng toán 2. Gii bng cách #t 'n ph$ .......................................................................... 25
Các thí d$ ................................................................................................... 25
Bài t%p t!ng t& ......................................................................................... 67
Dng toán 3. Gii bng cách s( d$ng tính !n iu c)a hàm s" ....................................... 77
Các thí d$ ................................................................................................... 77
Bài t%p t!ng t& ......................................................................................... 88
C – Phương trình & Bt phương trình logarit ..................................................................... 92
Dng toán 1. Gii bng cách a v cùng c! s" ............................................................... 92
Các thí d$ ................................................................................................... 93
Bài t%p t!ng t& ......................................................................................... 124
Dng toán 2. Gii bng cách #t 'n ph$ .......................................................................... 138
Các thí d$ ................................................................................................... 138
Bài t%p t!ng t& ......................................................................................... 154
Dng toán 3. S( d$ng tính !n iu hàm s" & B*t ng th+c .......................................... 164
Các thí d$ ................................................................................................... 165
Bài t%p t!ng t& ......................................................................................... 175
D – H phương trình & H bt phương trình m – logarit ................................................. 180
Dng toán 1. Gii h bng phép bi,n -i t!ng !ng .................................................... 180
Các thí d$ ................................................................................................... 180
Bài t%p t!ng t& ......................................................................................... 192
Dng toán 2. Gii h bng cách #t 'n ph$ ...................................................................... 197
Các thí d$ ................................................................................................... 197
Bài t%p t!ng t& ......................................................................................... 206
Dng toán 3. S( d$ng tính !n iu hàm s" & B*t ng th+c .......................................... 216
Các thí d$ ................................................................................................... 216
Bài t%p t!ng t& ......................................................................................... 226
E – Bài toán cha tham s m – logarit ................................................................................ 230
Các thí d$ ................................................................................................... 231
Bài t%p t!ng t& ......................................................................................... 250
www.MATHVN.com
www.DeThiThuDaiHoc.com
. . PT – BPT – HPT – HBPT /0123 451.67
Page - 1 -
A –  !"#$
%&'()*+,-'(./89:4"3&;!<=>4"3&3?5




%&'(),&/01'
: Cho

.

  

  
233%@@A
 
  
 

233&.B@B
 
 

  



 
 







 
*2*–,&/01'+3(*
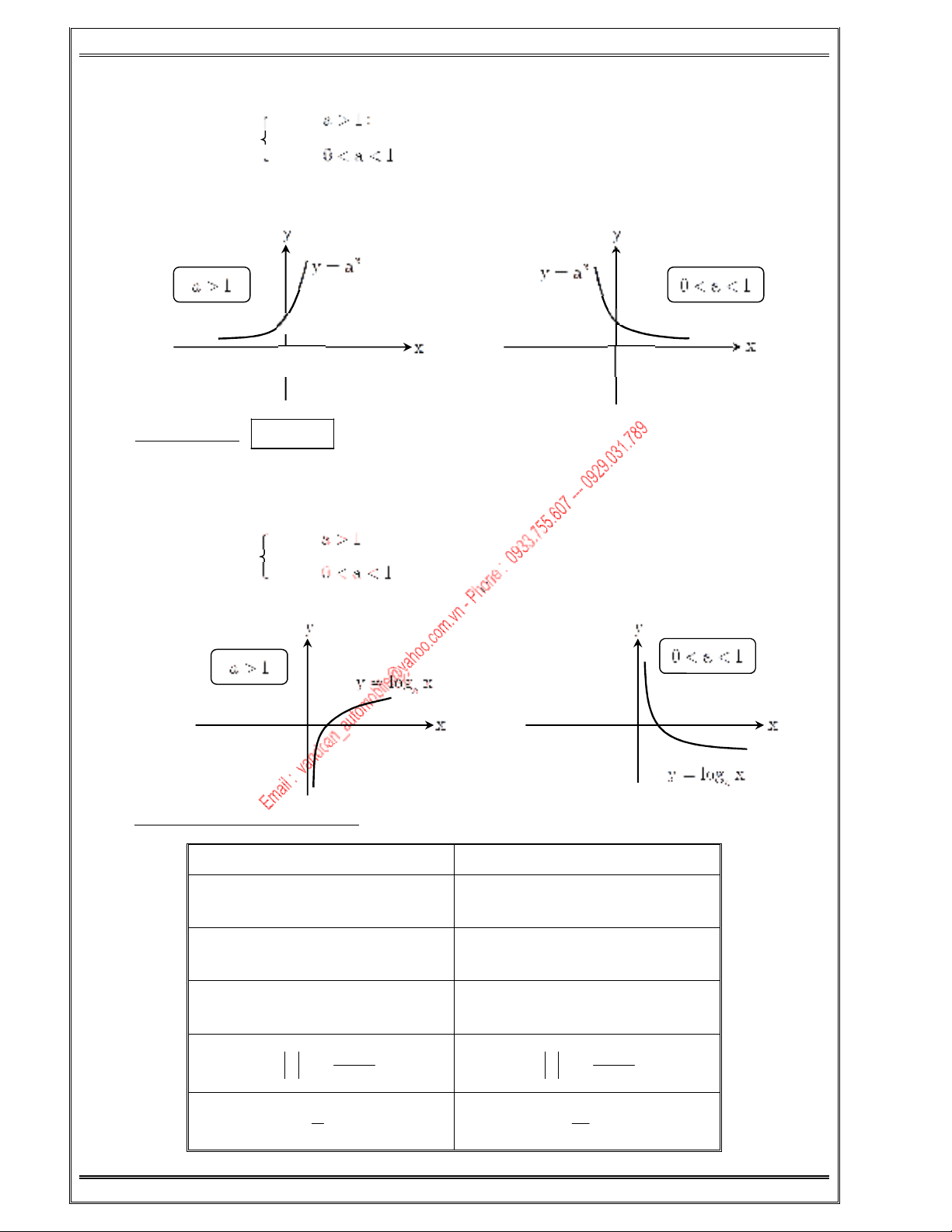
a/ Hàm s" m0
.
T%p xác Cnh:
.
n
4"
D

www.MATHVN.com
www.DeThiThuDaiHoc.com
. . –E–F–FE/0123 451.67
Page - 2 -
T%p giá trC:

.
Tính !n iu
Nh%n tr$c hoành làm tim c%n ngang.
Dng G thC:
b/ Hàm s" logarit
 .
T
%
p xác
C
nh:

.
T
%
p giá tr
C
:
.
Tính
!
n
i
u
Nh
%
n tr
$
c tung làm ti
m c
%
n
+
ng.
D
ng
G
th
C
c/
H)HH023

o hàm hàm s
"
s
!
c
*
p

o hàm hàm s
"
h
I
p
.








J Khi
hàm s" Gng bi,n.
J Khi : hàm s" nghCch bi,n.
J Khi : hàm s" Gng bi,n.
J Khi : hàm s" nghCch bi,n.
1
1
O O
O
1
O
1
www.MATHVN.com
www.DeThiThuDaiHoc.com
. . PT – BPT – HPT – HBPT /0123 451.67
Page - 3 -
B – 456!7–89456!7

I – :;<=68>
II – ?:@
(ABCDE K@!32L8
 
E3HM
J M8
.
JN8

nên:
 
.  !"#$"%
ư/+)F&)ơ2:
4(ươ&'0G(*:
:3+H003O ; .
6P 3L .
2QI@!4"N+'3L8 .
8'H(ươ&'0G(*:
:3+H003O ; .
, 3L .
, 3L .
2QI@!4"N+'3L .
&/01'(I/: .
1?
8R@!32L
<9*3@!32L
S#3 MT@!32LN
U5VM=S44:H3%@HP MT
%H3%@H3WI@5
www.MATHVN.com
www.DeThiThuDaiHoc.com