PHÒNG GD&ĐT HUY N BÌNH XUYÊNỆ
TR NG THCS THANH LÃNGƯỜ
CHUYÊN Đ NÂNG CAO CH T L NG THI TUY N SINH VÀO L P 10Ề Ấ ƯỢ Ể Ớ
MÔN:TOÁN
NĂM H C: 2021 - 2022Ọ
I. Tác gi chuyên đ, ch c v và đn v công tác:ả ề ứ ụ ơ ị
- H và tên: Nguy n Th Thu Huy nọ ễ ị ề
- Ch c v : Giáo viênứ ụ
- Đn v công tác: Tr ng THCS Thanh Lãng, TT Thanh Lãng, huy n Bình Xuyên, t nh Vĩnh ơ ị ườ ệ ỉ
Phúc.
II. Tên chuyên đ:ềGÓC VÀ T GIÁC N I TI PỨ Ộ Ế
III. Th c tr ng ch t l ng thi tuy n sinh vào 10 c a tr ng THCS Thanh Lãng năm h c ự ạ ấ ượ ể ủ ườ ọ
2021-2022:
Trong kì thi vào 10 năm h c 2021 - 2022, tr ng THCS Thanh Lãng có đi m xét tuy n x pọ ườ ể ể ế
th 36/145 c a t nh và x p th 2/14 c a huy n (sau tr ng Lý T Tr ng). Có th nói v i k tứ ủ ỉ ế ứ ủ ệ ườ ự ọ ể ớ ế
qu nh v y thì r t đáng t hào v i các em h c sinh khóa v a qua. ả ư ậ ấ ự ớ ọ ừ
Tuy nhiên, xét riêng môn Toán thì x p th 53/145 tr ng trên toàn t nh và th 2/14 tr ngế ứ ườ ỉ ứ ườ
c a huy n Bình Xuyên. Th t này so v i các tr ng THCS c a các huy n, thành ph lân c nủ ệ ứ ự ớ ườ ủ ệ ố ậ
nh Yên L c, Phúc Yên, Vĩnh Yên, … thì v n top cu i.ư ạ ẫ ở ố
Nguyên nhân chính là do h c sinh ch a xác đnh rõ m c tiêu h c t p, ch a c g ng h tọ ư ị ụ ọ ậ ư ố ắ ế
s c đ giành đc đi m đúng v i năng l c c a mình nên còn b r i r t đi m m t s ph nứ ể ượ ể ớ ự ủ ị ơ ớ ể ở ộ ố ầ
ki n th c và kĩ năng c b n.ế ứ ơ ả
IV. Đi t ng, d ki n s ti t d y:ố ượ ự ế ố ế ạ
- Đi t ng: H c sinh l p 9.ố ượ ọ ớ
- D ki n s ti t d y:12 ti tự ế ố ế ạ ế
V. H th ng (phân lo i, d u hi u nh n bi t đc tr ng) các d ng bài t p đc tr ng c a ệ ố ạ ấ ệ ậ ế ặ ư ạ ậ ặ ư ủ
chuyên đ:ề
1. D ng 1: Tính s đo các góc– s đo cungạ ố ố
2. D ng 2: Ch ng minh tam giác đng d ng, đng th c…thông qua ch ng minh các góc b ng ạ ứ ồ ạ ẳ ứ ứ ằ
nhau.
3. D ng 3: Ch ng minh t giác n i ti pạ ứ ứ ộ ế
VI. H th ng các ph ng pháp c b n, đc tr ng đ gi i các d ng bài t p trong chuyên ệ ố ươ ơ ả ặ ư ể ả ạ ậ
đ.ề
1. D ng 1: Tính s đo các góc – s đo cungạ ố ố
C n nh n di n đúng góc c n tính thu c lo i góc nào, m i quan h gi a t ng lo i góc v i s đo ầ ậ ệ ầ ộ ạ ố ệ ữ ừ ạ ớ ố
c a cung b ch n.ủ ị ắ
a) Góc tâm:ở
có đnh trùng v i tâm đng tròn đc g i là ỉ ớ ườ ượ ọ góc tâmở.
Cung n m bên trong góc đc g i là ằ ượ ọ cung b ch nị ắ .
Chú ý: Góc b t ch n n a đng tròn.ẹ ắ ử ườ
(s đo c a cung nh b ng s đo c a góc tâm ch n cung ố ủ ỏ ằ ố ủ ở ắ đó).
m
n
B
A
O
b) Góc n i ti p:ộ ế
có đnh n m trên đng tròn và hai c nh là hai dây cung đc g i ỉ ằ ườ ạ ượ ọ
là góc n i ti pộ ế .
Cung n m bên trong góc đc g i là ằ ượ ọ cung b ch nị ắ .
(s đo c a góc n i ti p b ng n a s đo c a cung b ch nố ủ ộ ế ằ ử ố ủ ị ắ ).
C
B
A
O
Tính ch tấ: Trong m t đng tròn:ộ ườ
Các góc n i ti p b ng nhau thì ch n các cung b ng nhau.ộ ế ằ ắ ằ
Các góc n i ti p cùng ch n m t cung ho c ch n các cung b ng nhau thì b ng nhau.ộ ế ắ ộ ặ ắ ằ ằ
Góc n i ti p (nh h n ho c b ng ) có s đo b ng n a s đo c a góc tâm cùng ch n m t ộ ế ỏ ơ ặ ằ ố ằ ử ố ủ ở ắ ộ
cung.
Góc n i ti p ch n n a đng tròn là góc vuông.ộ ế ắ ử ườ
c) Góc t o b i tia ti p tuy n và dây cung:ạ ở ế ế
ho c có đnh là ti p đi m, m t c nh là tia ti p tuy n và ặ ỉ ế ể ộ ạ ế ế
c nh còn l i là dây cung đc g i là ạ ạ ượ ọ góc t o b i tia ti p ạ ở ế
tuy n và dây cungế.
Cung đc g i là ượ ọ cung b ch n c a .ị ắ ủ
Cung đc g i là ượ ọ cung b ch n c a ị ắ ủ
(s đo c a góc t o b i ti p tuy n và dây cung b ng n a s ố ủ ạ ở ế ế ằ ử ố
đo c a cung b ch nủ ị ắ ).
Tính ch t: Trong m t đng tròn, góc t o b i tia ti p tuy n ấ ộ ườ ạ ở ế ế
và dây cung và góc n i ti p cùng ch n m t cung thì b ng ộ ế ắ ộ ằ
nhau.
d) Góc có đnh bên trong đng tròn:ỉ ở ườ
có đnh n m trong đng tròn , đc g i là ỉ ằ ườ ượ ọ góc có đnh bên ỉ ở
trong đng trònườ .
ch n hai cung và .ắ
.
(s đo c a góc có đnh bên trong đng tròn b ng n a t ng s đo ố ủ ỉ ở ườ ằ ử ổ ố
hai cung b ch n)ị ắ
n
m
E
D
C
O
A
B
e) Góc có đnh bên ngoài đng tròn:ỉ ở ườ
có đnh n m ngoài đng tròn , đc g i là ỉ ằ ườ ượ ọ góc có đnh bên ỉ ở
ngoài đng trònườ .
ch n hai cung và .ắ
.
(s đo c a góc có đnh bên ngoài đng tròn b ng n a hi u s ố ủ ỉ ở ườ ằ ử ệ ố
đo hai cung b ch n)ị ắ
2. D ng 2: Ch ng minh tam giác đng d ng, đng th c…thông qua ch ng minh các góc ạ ứ ồ ạ ẳ ứ ứ
b ng nhau:ằ
- Ch ng minh đc các góc b ng nhau d a trên m i quan h c a các lo i góc v i đng tròn,ứ ượ ằ ự ố ệ ủ ạ ớ ườ
m i quan h c a hai đng th ng song song, tam giác cân, hình thang cân, hình bình hành, hìnhố ệ ủ ườ ẳ
thoi, …. đ ch ng minh đc các c p tam giác đng d ng hay các đng th c gi a các đo nể ứ ượ ặ ồ ạ ẳ ứ ữ ạ
th ng, …ẳ
3. D ng 3: Ch ng minh t giác n i ti p:ạ ứ ứ ộ ế
D a vào các d u hi u c b n nh n bi t t giác n i ti p:ự ấ ệ ơ ả ậ ế ứ ộ ế
+ T giác có t ng hai góc đi b ng 180°.ứ ổ ố ằ
+ T giác có góc ngoài t i m t đnh b ng góc trong c a đnh đi di n.ứ ạ ộ ỉ ằ ủ ỉ ố ệ
+ T giác có b n đnh cách đu m t đi m (mà ta có th xác đnh đc). Đi m đó là tâm c aứ ố ỉ ề ộ ể ể ị ượ ể ủ
đng tròn ngo i ti p t giác đó.ườ ạ ế ứ
+ T giác có hai đnh k nhau cùng nhìn m t c nh ch a hai đnh còn l i d i m t góc .αứ ỉ ề ộ ạ ứ ỉ ạ ướ ộ
Chú ý: Đ ch ng minh m t t giác là t giác n i ti p ta có th ch ng minh t giác đó là m tể ứ ộ ứ ứ ộ ế ể ứ ứ ộ
trong các hình sau: Hình ch nh t, hình vuông, hình thang cân.ữ ậ
VII. H th ng các ví d , bài t p c th cùng l i gi i minh h a cho chuyên đ.ệ ố ụ ậ ụ ể ờ ả ọ ề
1. D ng 1: Tính s đo các góc – s đo cungạ ố ố
Ví d 1:ụ Cho hình v sau, tính s đo góc cung nh AB, bi t r nglà trung đi m.ẽ ố ỏ ế ằ ể
Gi i:ả
Tam giác vuôngcólà trung tuy n ng v i c nh huy nnên.ế ứ ớ ạ ề
Do đó là tam giác đu . Suy ra s đo cung nh là .ề ố ỏ
Ví d 2:ụ Cho hình v sau:ẽ
Tính s đo cung nh và t đó so sánh hai đo n th ngvà.ố ỏ ừ ạ ẳ
Gi i:ả
Xét tam giác vuông t icó nên .ạ
là góc ngoài c a tam giác cânnên .ủ
Xét có .
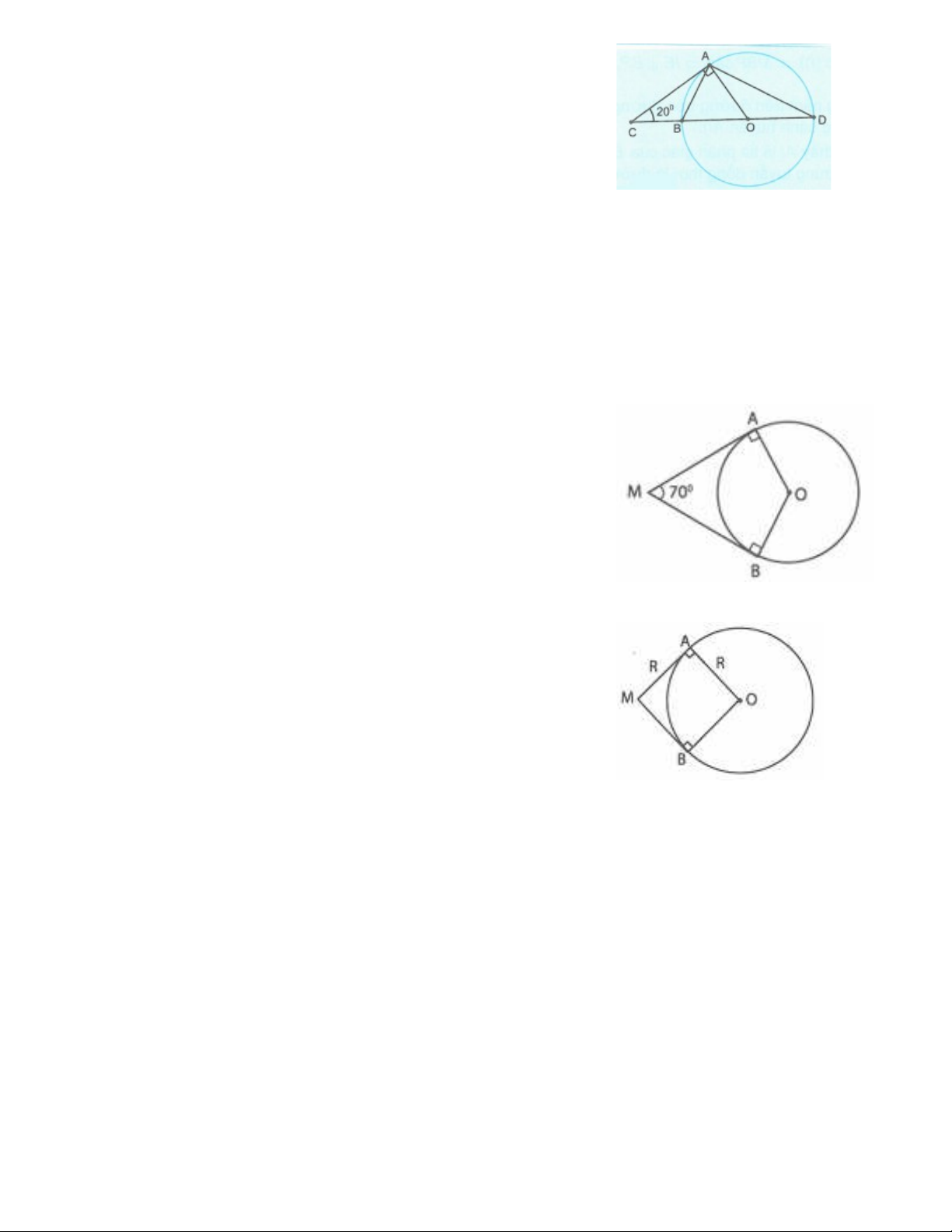
Ví d 3: ụCho đng tròn (O; R) và đi m M n m ngoài đng tròn đó. G i MA, MB là hai ti p ườ ể ằ ườ ọ ế
tuy n v i đng tròn t i A và B. Tính s đo c a góc tâm t o b i hai bán kính OA và OB n u:ế ớ ườ ạ ố ủ ở ạ ở ế
a) b) c)
Gi i:ả
Vì MA và MB là các ti p tuy n c a đng tròn (O) t i A và B nên: .ế ế ủ ườ ạ
Suy ra
a)
Xét t giác MAOB có:ứ
V y s đo góc tâm t o b i hai bán kính OA, OB b ng ậ ố ở ạ ở ằ
110°.
b)
Xét ∆MAO có: và
∆MAO vuông cân t i A.ạ
Do MA, MB là hai ti p tuy n c t nhau t i M nênế ế ắ ạ
V y s đo góc tâm t o b i hai bán kính OA, OB b ng 90°.ậ ố ở ạ ở ằ
c)
Xét ∆MAO vuông t i A có: ạ
Do MA, MB là hai ti p tuy n c t nhau t i M nênế ế ắ ạ
V y s đo góc tâm t o b i hai bán kính OA, OB b ng ậ ố ở ạ ở ằ
120°.
Ví d 4: ụ
Xem hình v (hai đng tròn có tâm là B, C và đi m B n m ẽ ườ ể ằ
trên đng tròn tâm C).ườ
a) Bi t . Tính ế
b) N u = 136ế0 thì có s đo là bao nhiêu?ố
Gi i:ả
a) Đng tròn tâm B cólà góc n i ti p ch n cungườ ộ ế ắ MN; là góc
tâm ch n cungở ắ MN nên
Đng tròn tâm C cóườ là góc n i ti p ch n cungộ ế ắ PQ; là góc tâm ch n cungở ắ PQ nên:
b) Ta có: nên = : 4 = 1360 : 4 = 340.
2. D ng 2: Ch ng minh tam giác đng d ng, đng th c…thông qua ch ng minh các góc ạ ứ ồ ạ ẳ ứ ứ
b ng nhau.ằ
Ví d 1: ụ
Cho đng tròn (O) và đi m M n m bên ngoài đng tròn đó. Qua đi m M k ti p tuy n MT ườ ể ằ ườ ể ẻ ế ế
và cát tuy n MAB.Ch ng minh MTế ứ 2 = MA.MB.
Gi i:ả
là góc t o b i tia ti p tuy n và dây cung ch n cung AT c a ạ ở ế ế ắ ủ
đng tròn (O); haylà góc n i ti p ch n cung AT c a đngườ ộ ế ắ ủ ườ
tròn (O), do đó:
và cóvàchung nên
(g - g)
hay(đpcm)
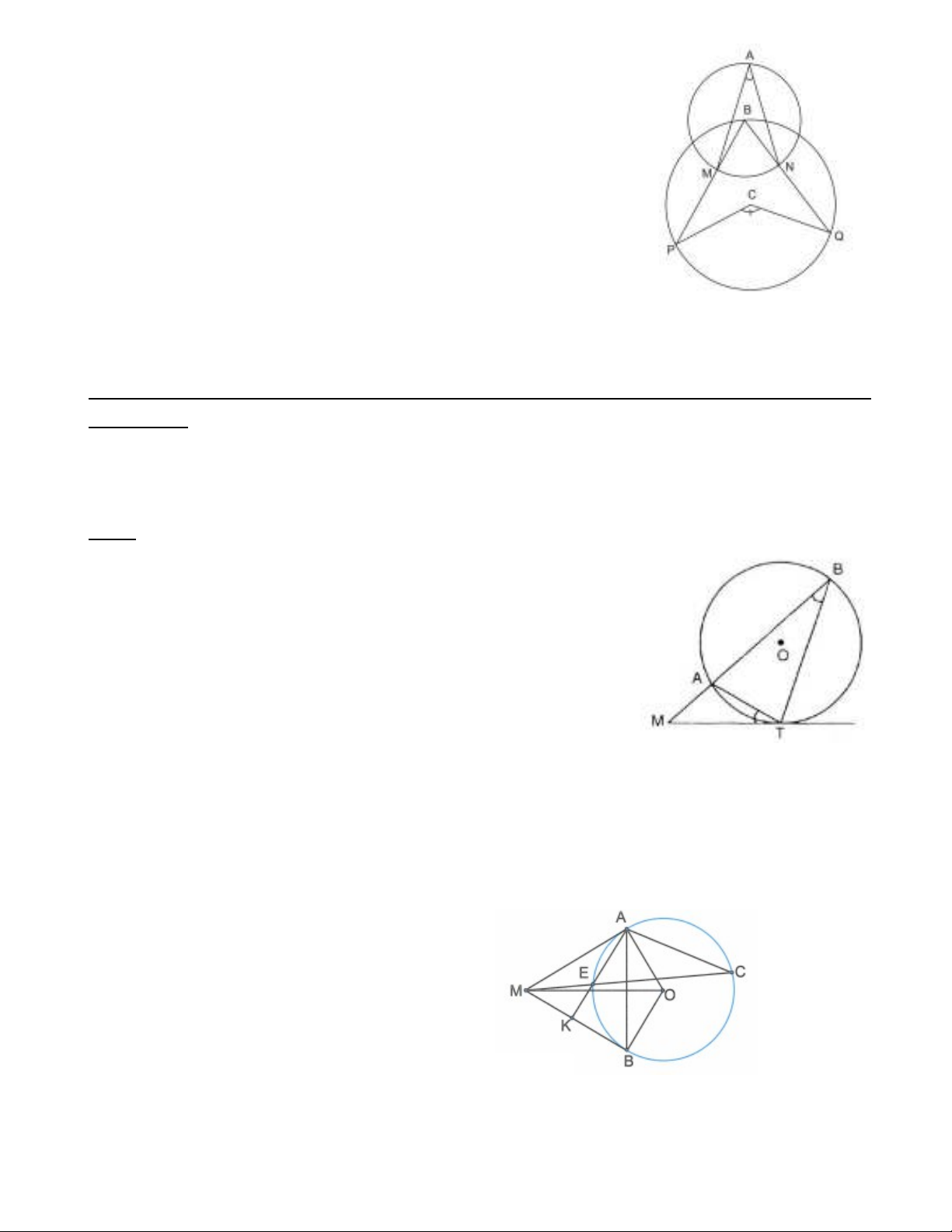
Ví d 2:ụ Gi s vàlà hai đi m phân bi t trên đng tròn. Các ti p tuy n c a đng tròn ả ử ể ệ ườ ế ế ủ ườ
t ivàc t nhau t i đi m. T k đng th ng song song v i c t đng trònt i . c t đng tròn ạ ắ ạ ể ừ ẻ ườ ẳ ớ ắ ườ ạ ắ ườ
t i . Các tiavà c t nhau t i. ạ ắ ạ
Ch ng minh r ng và .ứ ằ
Gi i:ả
Do nên (hai góc so le trong).
Ta l i có(góc n i ti p và góc t o b i tia ti p ạ ộ ế ạ ở ế
tuy n và dây cung cùng ch n).ế ắ
Do đó .
Xét và có: (ch ng minh trên); chung.ứ
Suy ra
(đpcm) (1)
Ta th y (góc n i ti p và góc t o b i tia ti p tuy n và dây cung cùng ch n ).ấ ộ ế ạ ở ế ế ắ
T đó (2)ừ
T (1) và (2) suy ra nghĩa là (đpcm).ừ