tr−êng §H hång ®øc
Khoa Khoa häc tù nhiªn
§¸p ¸n - thang ®iÓm
®Ò thi thö ®¹i häc, cao ®¼ng – n¨m 2009
§Ò Thi chÝnh thøc
M«n TOÁN, Khèi B
(§¸p ¸n – Thang ®iÓm cã 5 trang)
Câu I: (2 điểm)
Ý Nội dung Điểm
1) Khảo sát và vẽ đồ thị hàm số
42
yx 2=− +4x 1,0
+) Tập xác định +) Đạo hàm
\32
8x=−
x = 0
y4x
′
⇔
hoặc x = 2±
y' = 0 0,25
+) Bảng biến thiên
x
+
−
∞ - 2 2
0 ∞
y’ - 0 + 0 - 0 +
+
∞ 2
+
∞
y
-2 -2
0,5
+) Đồ thị: Đồ thị nhận 0y làm trục đối xứng.
-2 -1 1 2
x
y
0
1
2
-2
42
y
x4x+2
=
2
2−
-1
−
0,25
2) Tìm m để có ba điểm cực trị lập thành một tam giác có một góc 12 .
422
yx 2mx m m=+ + + 0D1,0
Ta có ;
3
=+
()
y4x4mx
′2x 0
y0 4xx m 0 xm
=
⎡
′=⇔ + =⇔
⎢
=
±−
⎣ (m<0) 0,25
Gọi A(0; m2+m); B( m−m−
; m); C(- ; m) là các điểm cực trị.
2
AB ( m; m )=−−
G
JJJ
; 2
( m; m )=−− −
JJJG
0D
l
A
AC . Tam giác ABC cân tại A nên góc 12 chính là . 0,25
l
A120=D
l
4
4
1AB.AC 1 m.mm 1
cosA 22mm2
AB . AC
−− − +
⇔=−⇔ =−⇔ =−
−
JJJG JJJG
JJJG JJJG 0,25
4
444
4
3
m0
mm 1 2m 2m m m 3m m 0 1
m
mm 2 3
=
⎡
+⎢
⇔=−⇒+=−⇔+=⇔
⎢=−
−⎢
⎣
(lo¹i do ®k m<0)
Vậy m= thỏa mãn bài toán.
0,25
3
1
3
−
Câu II: (2 điểm)
Ý Nội dung Điểm
1) Giải bpt:
()
(
11 x 2+ +x-3
)
2
x3 x 4+− − ≥ (1) 1,0
Điều kiện .
≥x1
Nhân hai vế của bpt với x3 x1++ −, ta được
(1)
2
()
()
22
4. 1 x 2 4. x 3 x 1 1 x 2 x 3 x 1x-3 x-3⇔++ ≥ ++−⇔++ ≥++−
0,25
22 22
x2 2x2 2 2 x x-2
x-2 x-3 x+2 x-3 - 4 0 x2
2x
≤
⎡
++ +≥ + +⇔ ≥⇔
⎢≥
⎣ 0,5
Kết hợp với điều kiện x ta được . ≥1x2≥0,25
2) Giải pt:
()
41sin2x 1
cos x
⎜⎟
⎝⎠
+=
2sin x
tanx
π
⎛⎞
−
+ (2) 1,0
Điều kiện co .
s x 0 x k , k
2
π
≠⇔≠ +π∈]
Ta có (1)
()
2
cosx sinx cosx sinx
cos x sin x
cosx cosx
−+
⇔+=
0,25
()()()
cosx sinx cosx sinx cosx sinx 1 0
⎡⎤
⇔+ − +−=
⎣⎦
)
)
x sin x cos 2 1 0xcos
⇔
+−=
0,25
cos x sin x 0 tan x 1 xm
4
cos 2 1 0 cos 2 1 m
xx
x
π
⎡
+= =− =− + π
⎡⎡
⎢
⇔⇔⇔
⎢⎢
⎢
−= =
⎣⎣
=π
⎢
⎣
,m∈].
Dễ thấy họ nghiệm trên thỏa mãn điều kiện. Đáp số: xm
,m
4
mx
π
⎡=− + π
⎢
∈
⎢=π
⎢
⎣
].
0,25
Câu III: (1 điểm)
Ý Nội dung Điểm
Tính tích phân:
2
ex 2009+
1
Ilnxdx
x
=∫. 1,0
Đặt tx= x 1 e2
2
txdx2t.dt⇒=⇒ = t 1 e
0,25
e2
t 2009+
=
()
1
2 t 2009 .ln t.dt+
∫
1
I2 .t.lnt.dt
t
∫=
e
20,25
Đặt
()
23
dv t 2009 dt t
v3
=+
⎪⎪
⎩=+
⎪
⎩
dt
du
ulnt t
2009t
⎧=
=
⎧⎪
⎪⎪
⇒
⎨⎨
, ta có:
e
32
tt
I 2 2009t ln t 2 2009 .dt
33
⎛⎞⎛
=+ − +
⎜⎟⎜
⎜⎟⎜
∫
1
⎞
⎟
⎟
⎝⎠⎝⎠
e
33
e
1
1
et
2 2009e 2 2009t
39
⎛⎞
⎛⎞
⎜⎟
=+ − +
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
0,5
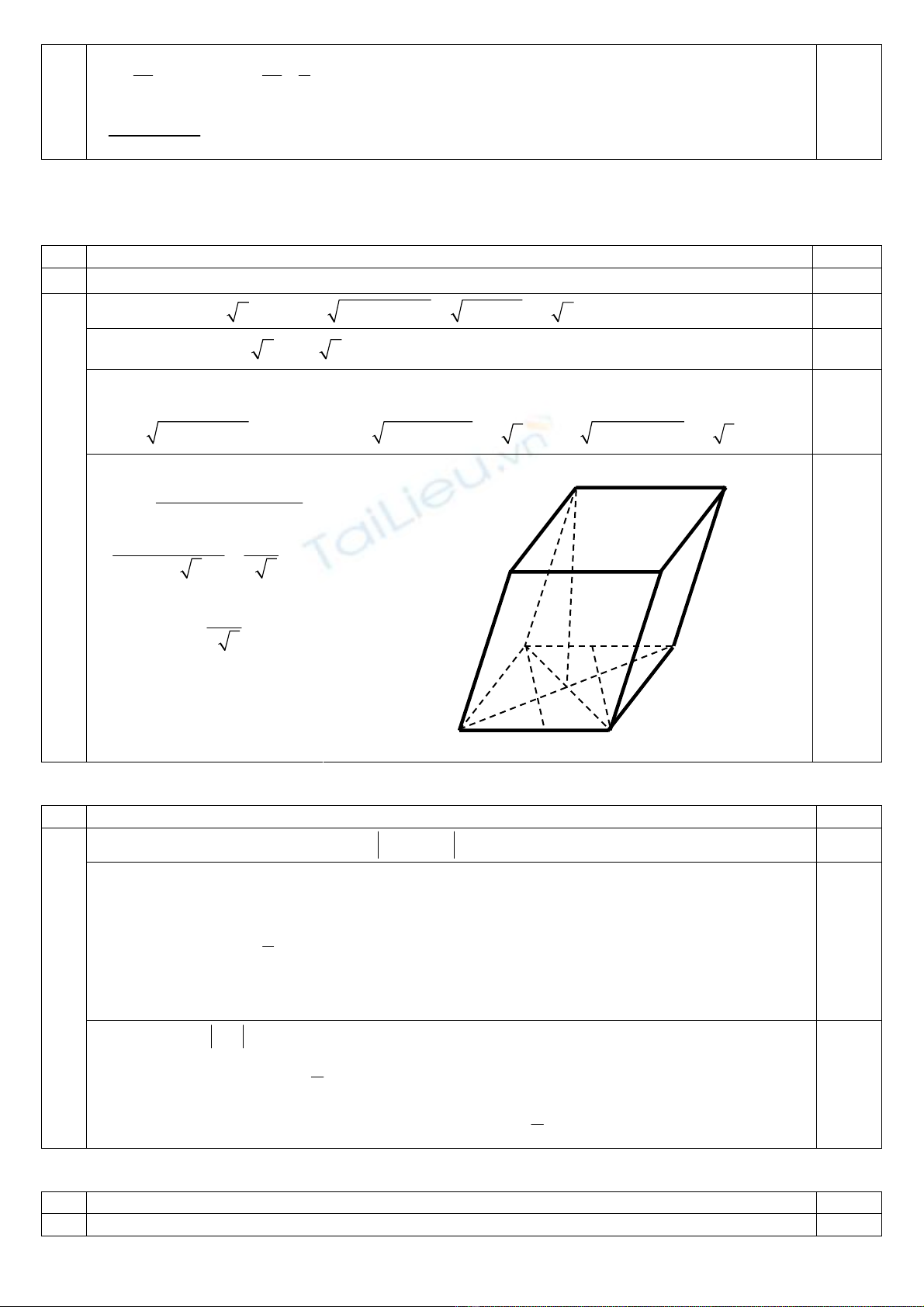
33
ee1
⎛⎞⎛
2 2009e 2 2009e 2009
399
⎞
=+ −−+ −
⎜⎟⎜ ⎟
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
=
3
4e 36164
9
+
Câu IV: (1 điểm)
Ý Nội dung Điểm
Hình học không gian 1,0
Ta có AO=OC=a 22
AO 4 a 2
222
AA a -2a
′′
− = =AO⇒= 0,25
Suy ra V=B.h= 42
2
42
3
a=a.a (đvtt) 0,25
Tính góc giữa AM và AC
′
. Gọi N là trung điểm AD, suy ra //CN.
AM
ACN
′
Xét tam giác ta có
222
AC OC 2 BM a 5; AN a 3
′′ ′ ′
=+= += =−=
222
A O a; CN=AM= AB AAAN .
0,25
Suy ra
3
22 2
222
CA CN A N
cos C 2.CA .CN
53 30
.a 5 2 5
′′
+−
=′
+−
==>
4a a a
a
AC
′
2.2
Vậy cosin của góc giữa AM
và bằng 3
25
.
A
′
D′
B
′
C 2a
′
A N D
2a
O
B C
M
0,25
Câu V: (1 điểm)
Ý Nội dung Điểm
Đặt với
tsi=
[
nx
]
t1,1∈− ta có 32
A= 5t -9t +4 . 0,25
Xét hàm số với f(t) 32
5t -9t +4=
[
]
t1,1∈−
(5t-6)
.
Ta có f (t) 1 2
5t -18t=3t
′=
6
f(t) 0 t 0 t
′=⇔=∨=
5
f( 4−= =
(loại)
1) 10,f(1) 0,f(0)− = .
Vậy .
10 f (t) 4−≤ ≤
0,5
Suy ra 0A f(t)10≤= ≤. Vậy GTLN của A là 10 đạt được khi
t1sinx1x 2
π
=− ⇔ =− ⇔ =− +k2π
và GTNN của A là 0 đạt được khi t1 sinx1 x k2
2
π
=⇔ =⇔ = + π
.
0,25
Câu VIa: (2 điểm)
Ý Nội dung Điểm
1) Hình học phẳng
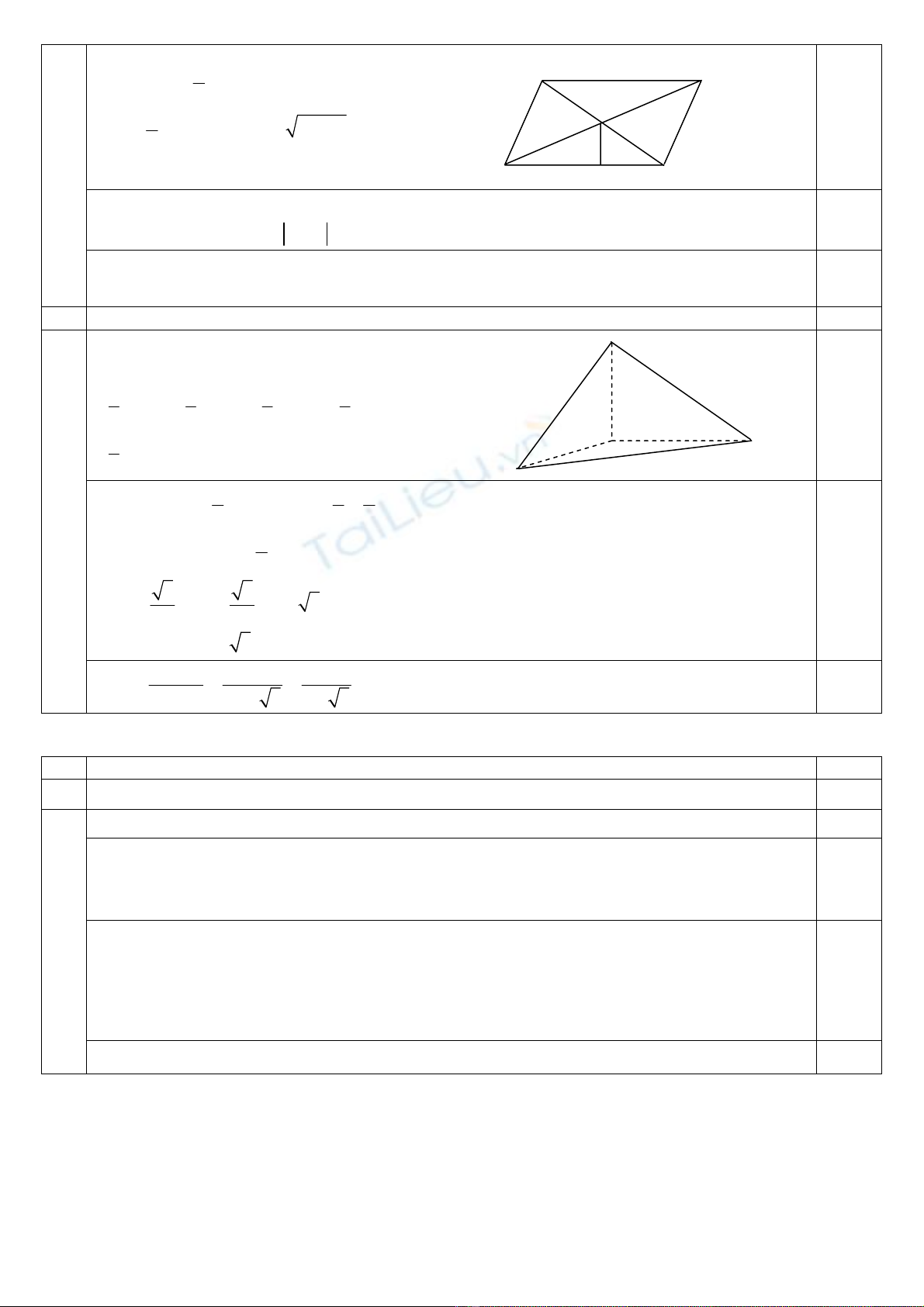
IAB ABC
1
Ta có SS. Mặt khác
4D=1=
4
IAB
1
S.IH.IB=2 với AB= 22
10 1+=
H
.
Suy ra IH=2.
D
C
I
A B
0,25
Gọi vì I thuộc đường thẳng y=x+1, ta có phương trình đường thẳng AB là y=0;
II
I(x , x 1)+
IH=2 I
d(I/ AB) 2 x 1 2.⇔=⇔+=
0,25
TH1:
I
I
x 3 I( 3; 2);C( 8; 4);D( 9; 4).=− ⇒ − − − − − −
x 1 I (1; 2) ; C( 0; 4); D ( 1; 4) .=⇒ −
TH2: 0,5
2) Hình học không gian
Gọi I là mặt cầu nội tiếp tứ diện OABC ta có:
OABC I
VV
OAB IOBC OCA ABC
+V +V +V=
=OAB
.r.S OBC OCA ABC
1111
.r.S .r.S .r.S
3333
+++
=TP
1.r.S
3.
C
O
B
A
0,25
Lại có OABC
18
V .OA.OB.OC
66
==
4
3
=
(đvtt)
OAB OBC OCA
1
SSS .OA.
2
=== OB2=
(đvdt)
2
ABC
33
SAB.823
===
44 (đvdt)
Suy ra TP 23=+S6 (đvdt)
0,5
Do đó OABC
TP
3V 42
S623 3 3
==
++
(đv độ dài) 0,25
Câu VIIa: (1 điểm)
Ý Nội dung Điểm
Chứng minh
010 1 9 91 100 10
10 20 10 20 30
C.C C.C C++=
10 20 10 20
C.C C.C++"
Ta có (1)
30 10 20
(1 x ) (1 x ) .(1 x ) , x+=+ +∀∈\0,25
Lại có .
n
30
x ) k k
30
k1
(1 C .x , x
=
+= ∀∈
∑\
10
x30
(1 x )+10
10 30
aC=
Vậy hệ số của khai triển của là .
10
a
0,25
Lại có
() )
10 20
0 1 9 9 10 10 0 20 20
10 10 10 20 10 20 20 10 20
(1 x ) .(1 x )
C Cx Cx Cx C Cx Cx Cx Cx Cx
++=
⎡⎤
= + ++ + + ++ + + ++
⎣⎦
"""
010 1 9 91 100
10 20 10 20 10 20 10 20
C.C C.C C.C C.C++++"
()(
1 10 10 11 11 12 12
10
Hệ số của x10 trong khai triển này là b10 =
0,25
Do (1) đúng với mọi x nên . Suy ra điều phải chứng minh.
10 10
ab=0,25
Theo chương trình nâng cao
Câu VIIb: (2 điểm)
Ý Nội dung Điểm
1) Hình học phẳng
Đường tròn đã cho có tâm I(1;2) và bán kính
R= 10 . Suy ra AI
2.IH=
JJG JJG
H
12(X 1) 37
=−
⎧⎛⎞
H
H;
32(Y 2) 22
⇔⇔
⎨⎜⎟
=− ⎝⎠
⎩
ABCΔ
Gọi H là trung điểm BC, ta có I là trọng tâm
tam giác ABC vì là tam giác đều.
A
I*
B H C
0,25
Pt BC đi qua H và vuông góc với AI là: (BC): 37
1. x 3. y 0
22
⎛⎞⎛⎞
−
+−=
⎜⎟⎜⎟
⎝⎠⎝⎠
x3y120⇔+ − =
0,25
Vì B, C thuộc đường tròn đã cho nên tọa độ của B, C lần lượt là các nghiệm của hệ pt:
22 22
xy2x-4y-5=0
x+3y-12=0
+− xy2x-4y-5=0
x=12 - 3y
⎧⎧
+−
⇔
⎨⎨
⎩⎩
0,25
Giải hpt trên ta được: 3337 3 3337 3
B;;C;
⎛⎞⎛⎞
−+ +−
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠
22 22
⎝⎠
hoặc ngược lại. 0,25
2) Hình học không gian
Gọi I(t; -t; 0)∈, chọn M(5; -2; 0)∈ ta có
1
d2
d;t 2;0)−IM (5 t=−
J
JJG
Vector chỉ phương của đường thẳng d2 là 2
d
u ( 2; 0;1)=−
G
Suy ra
2
d
IM, u (t 2;t 5;2t 4)
⎡⎤
=− − −
⎣⎦
JJJGG 0,25
Do đó 2
2
6t 30t 45
2
d
2
d
IM, u
I / d ) 5
u
⎡⎤ −+
⎣⎦
==
JJJGG
G
d( 0,25
Theo bài ra d( 2
2
6t 30t 45 3
5
−+=2
6t 30t 0I / d ) 3=
⇔
⇔
−= 0,25
()( )
⎡⇒
=
⎡⎢
⇔⇔
⎢=⎢
⎣−⇒
⎣
222
22
2
I(0;0; 0) pt mÆt cÇu (S):x +y +z =25
t0
t5 I(5; 5;0)
p
t mÆt cÇu (S): x-5 +
y
+5 +z =25
0,25
Câu VIb: (1 điểm)
Ý Nội dung Điểm
Ta có
()
10 5
10 5
10 5
10 10
10
(1 i3) 44
2.cos isin
33
77
2 . cos isin .2 . cos isin
(1 i) ( 3 i) 44 66
z
π
πππ
⎛⎞⎛⎞
++
⎜⎟⎜⎟
−+ ⎝⎠⎝⎠
==
−− ππ
⎛⎞
+
⎜⎟
⎝⎠
0,5
10
10
35 35 5 5 55 55
2 . cos isin . cos i sin cos i sin
2266 33
cos 5 sin 5 1
40 40
40 40 cos i sin
2.cos isin 33
33
ππππ
⎛⎞⎛⎞
ππ
++ +
⎜⎟⎜⎟
⎝⎠⎝⎠
===π+π=−
ππ
ππ
⎛⎞ +
+
⎜⎟
⎝⎠
Vậy z là số thực.
0,5
------------------------------- Hết -----------------------------
5