Đ c ng ôn t p lý thuy t đi u khi n t đ ngề ươ ậ ế ề ể ự ộ
I. Lý thuy tế
Câu 1: Th nào là h th ng đi u khi n? C u trúc h th ng đi u khi n?ế ệ ố ề ể ấ ệ ố ề ể
L y các ví d v các h th ng đi u khi n ( Phân tích các thành ph nấ ụ ề ệ ố ề ể ầ
h th ng, đ u vào đ u ra, ph n h i mà không quan tâm đ n hàm truy n).ệ ố ầ ầ ả ồ ế ề
Câu 2: Mô hình toán h c là gì ? Các ph ng pháp mô hình toán h c họ ươ ọ ệ
th ng đi u khi n?ố ề ể
Câu 3: Hãy trình bày v phép bi n đ i laplace? Các tính ch t c a phépề ế ổ ấ ủ
bi n đ i laplace. T i sao th ng dùng phép bi n đ i laplace thay ph ngế ổ ạ ườ ế ổ ươ
trình vi phân trong tính toán?
Câu 4: T i sao h th ng n đ nh khi các nghi m n m bên trái c a m tạ ệ ố ổ ị ệ ằ ủ ặ
ph ng ph c. Tín hi u ra c a h th ng dao đ ng khi nào?ẳ ứ ệ ủ ệ ố ộ
Câu 5: Phân tích s khác nhau gi a tiêu chu n n đ nh t n s và tiêuự ữ ẩ ổ ị ầ ố
chu n n đ nh đ i s ? ẩ ổ ị ạ ố
Câu 6: Trình bày ph ng pháp v bi u đ bode và bi u đ Nyquist c aươ ẽ ể ồ ể ồ ủ
h th ng? Hãy nêu tiêu chu n n đ nh bode và tiêu chu n n đ nhệ ố ẩ ổ ị ẩ ổ ị
Nyquist?
Câu 7: Các ch tiêu đánh giá ch t l ng c a khâu quán tính b c nh t?ỉ ấ ượ ủ ậ ấ
Câu 8: Nêu các tiêu chu n t i u hóa đáp ng quá đ , trong các tiêuẩ ố ư ứ ộ
chu n trên thì tiêu chu n nào đ c s d ng nhi u nh t? vì sao.ẩ ẩ ượ ử ụ ề ấ
Câu 9: Hãy phân tích tác d ng c a b đi u khi n? Nêu nh h ng c aụ ủ ộ ề ể ả ưở ủ
khâu hi u ch nh s m pha, tr pha, s m tr pha t i h th ng đi u khi n?ệ ỉ ớ ễ ớ ễ ớ ệ ố ề ể
Câu 10: Hãy phân tích các tác đ ng c a các khâu P,PI, PD, PID t i hộ ủ ớ ệ
th ng đi u khi n?ố ề ể
II. Bài t p: ậ
Câu 1: Th c hi n các phép bi n đ i Laplace ng c đ i v i các h th ngự ệ ế ổ ượ ố ớ ệ ố
có hàm truy n nh sau:ề ư
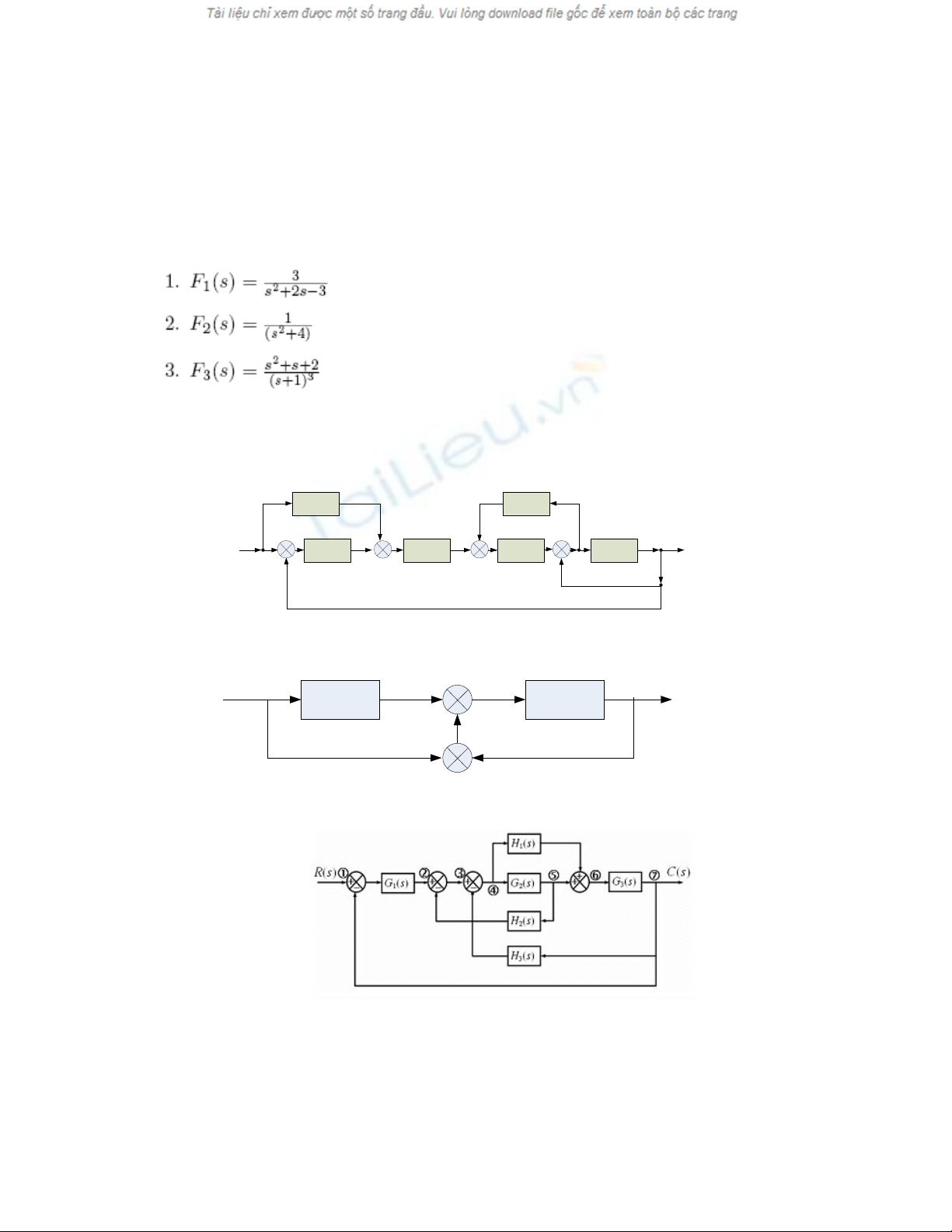
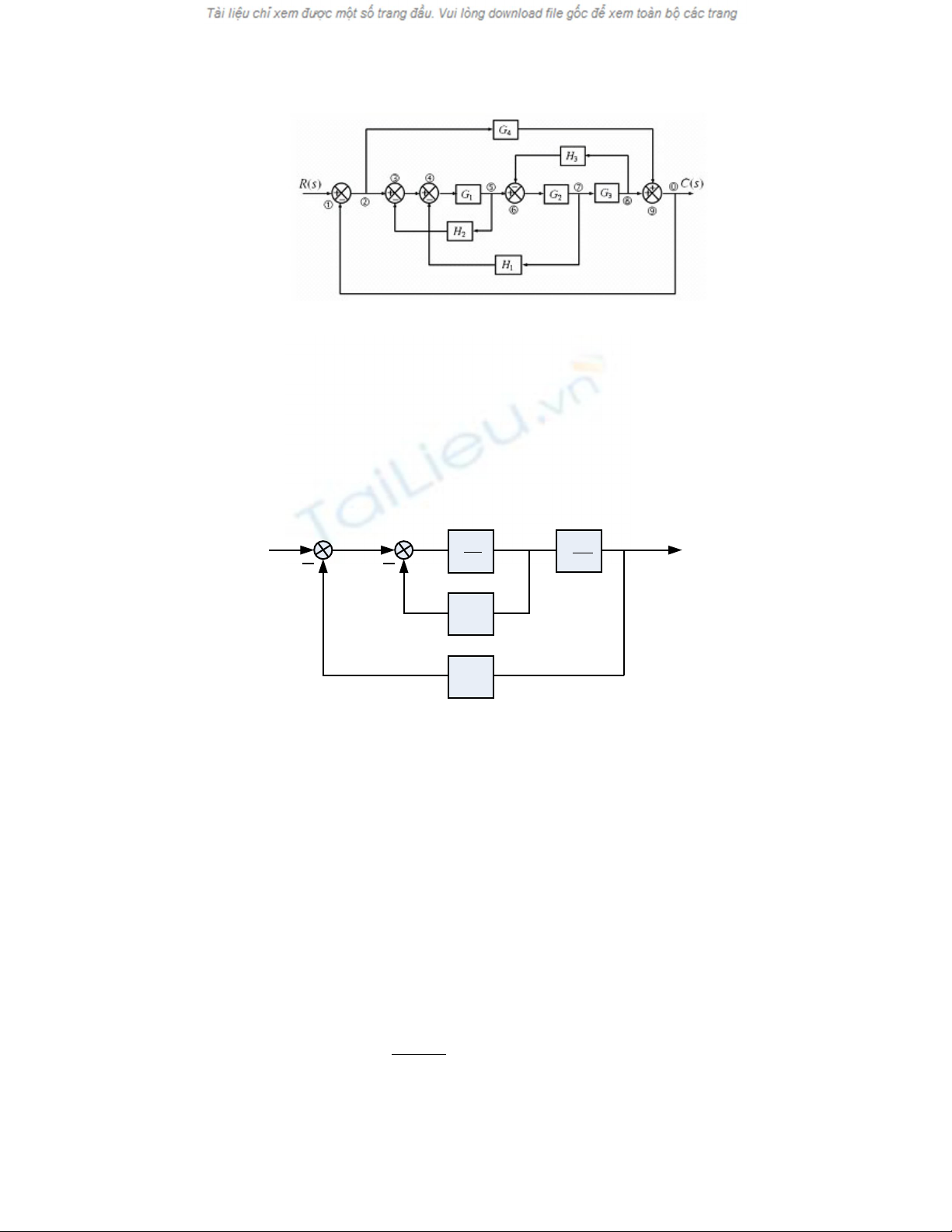
Câu 2: S d ng ph ng pháp bi n đ i s đ kh i và s đ dòng tín hi uử ụ ươ ế ổ ơ ồ ố ơ ồ ệ
(áp d ng công th c Mason) tìm hàm truy n c a các h th ng sau:ụ ứ ề ủ ệ ố
a.
b.
c.
d.
Y
1H
2H
3H4H5H
6H
+
+
+
+
+
−
+
−
X
+
+
X
Y
2H
−
−
Câu 3: S d ng tiêu chu n Routh – Hurwitz đ xét s n đ nh c a hử ụ ẩ ể ự ổ ị ủ ệ
th ng có ph ng trình đ c tính sau: ố ươ ặ
a.
03482
234
=++++
ssss
b.
0243
2345
=+++++
sssss
Câu 4: Cho h th ng có K1=1; K2=4; K3=2; K4=6ệ ố
R(s)
K3
s
K1
s
K2
K4
E(s) Y(s)
U(s)
Hình 5: S đ kh i h th ngơ ồ ố ệ ố
a. Tìm hàm truy n m ch kín: Y(s)/U(s)ề ạ
b. Xác đ nh tín hi u đ u ra khi tín hi u đ u vào U(s) là m t hàm xungị ệ ầ ệ ầ ộ
đ n vơ ị
c. S d ng tiêu chu n Routh – Hurwitz kh o sát tính n đ nh h th ng ử ụ ẩ ả ổ ị ệ ố
Câu 5: V bi u đ bode và kh o sát n đ nh h th ng theo tiêu chu nẽ ể ồ ả ổ ị ệ ố ẩ
bode các tr ng h p sau: ườ ợ
1. G(s) =
)1(
1
+ss
2. G(s) =
)1(
1
2+ss
3. G(s) =
10
1
2++
+
ss
s
4. G(s) =
10
1
+
+
s
s
5. G(s) =
)1)(10010(
1
2+++ sss
6. G(s) =
)10010)(1(
)11.0(1000
2+++
+
ssss
s
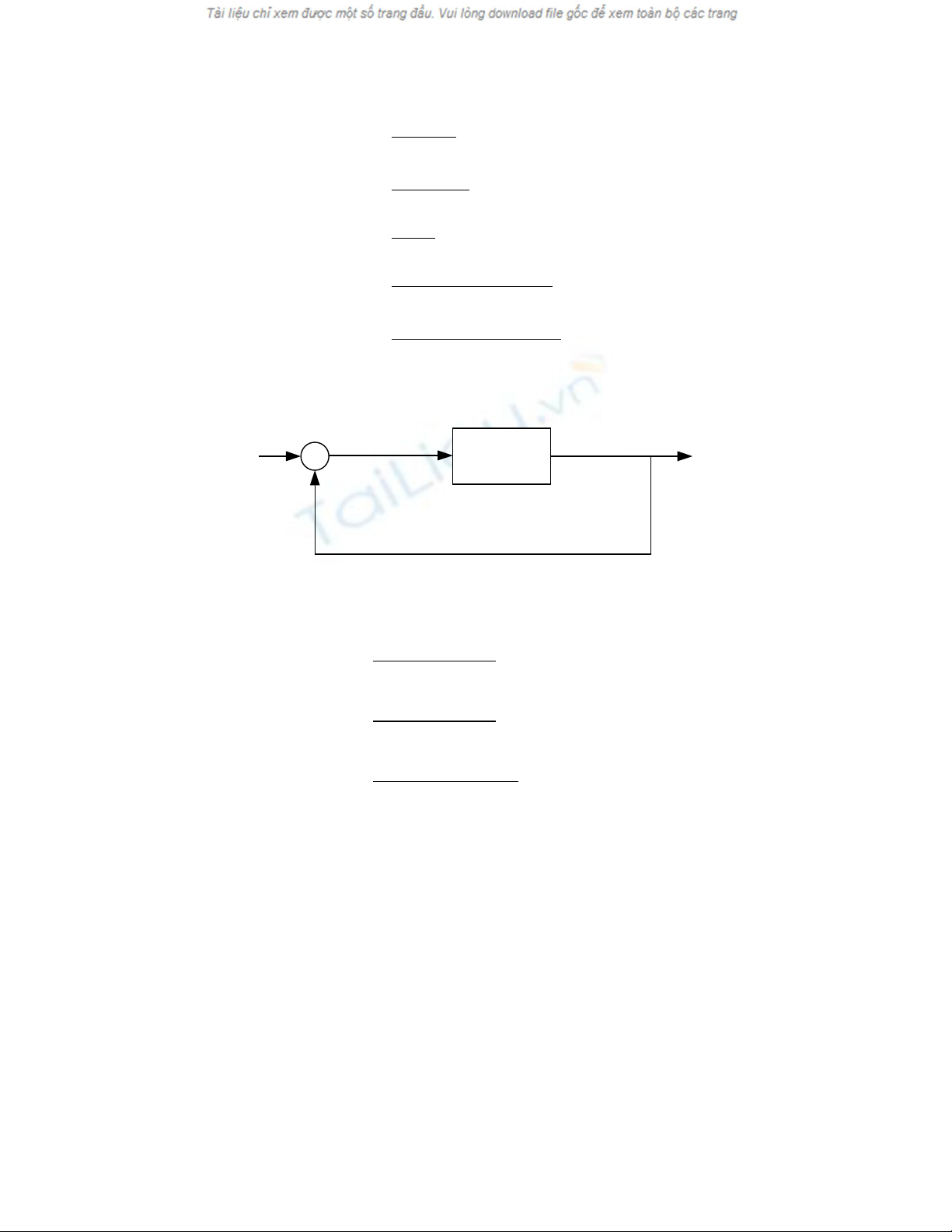
Câu 6: Cho s đ kh i c a h th ng kín sau: ơ ồ ố ủ ệ ố
)(sG
h
X y
-
Hãy xác s n đ nh c a h th ng b ng tiêu chu n Nyquist c a hự ổ ị ủ ệ ố ằ ẩ ủ ệ
th ng kín ? ố
-
)13)(12(
1
)(
++
=
ss
sG
h
-
)12)(1(
1
)(
+−
=
sss
sG
h
-
1253
1
)(
24
+++
=
sss
sG
h
Câu 7: Xác đ nh sai s xác l p c a h th ng v i các tính hi u vào r(t)=ị ố ậ ủ ệ ố ớ ệ
dir c(t); r(t)=1(t); r(t)=tắ
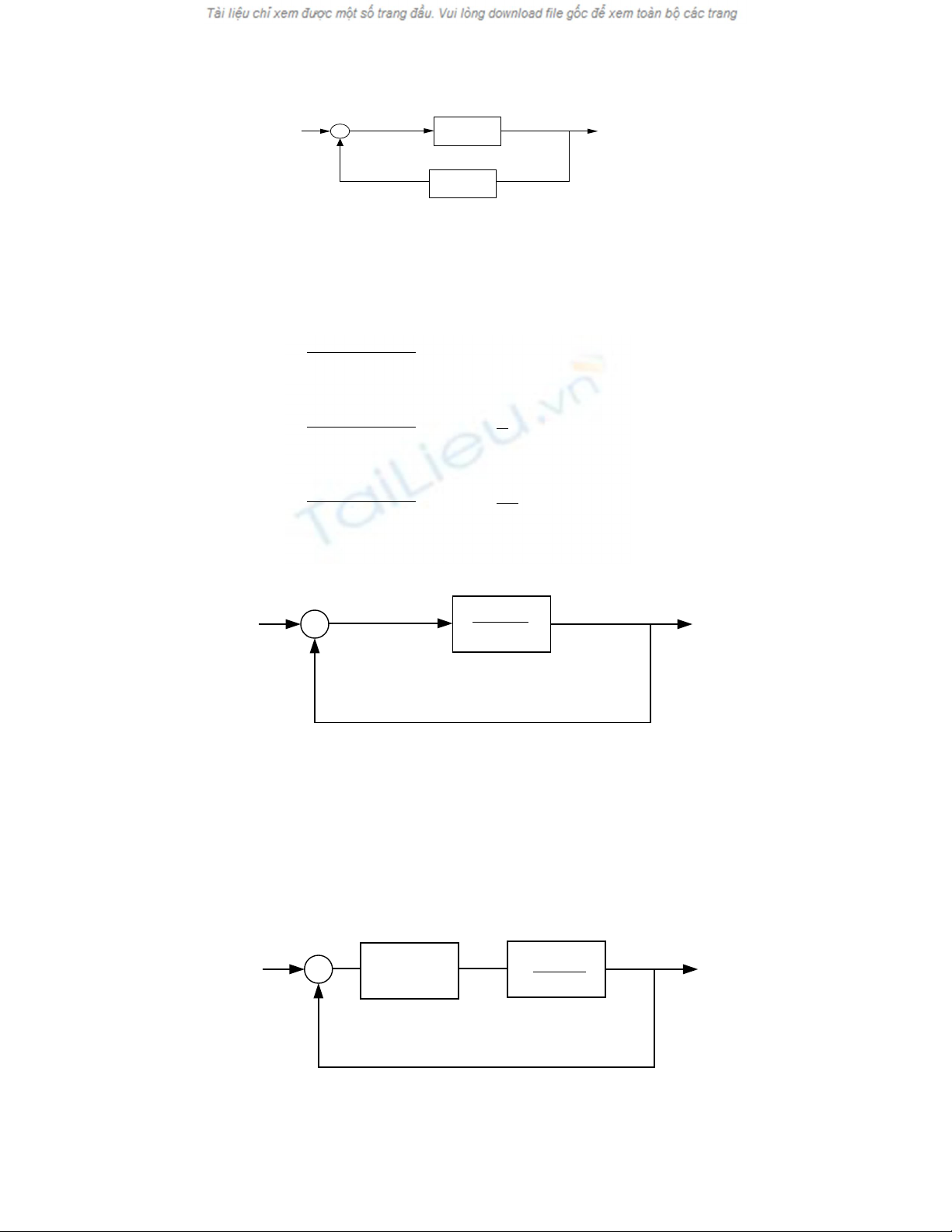
)(sG
R(s) C(s)
-
)(sH
E(s)
Trong đó :
-G(s)=
)5)(1(
2
++
+
ss
s
; H(s)= s+3;
-G(s)=
)5)(1(
2
++
+
ss
s
; H(s)=
s
1
-G(s)=
)5)(1(
2
++
+
ss
s
; H(s)=
2
1
s
Câu 8: Cho h th ng có d ng nh hình v :ệ ố ạ ư ẽ
R(s) C(s)
-
)2(
4
+ss
a) Hãy xác đ nh h s t t d n ζ, t n s dao đ ng riêng wị ệ ố ắ ầ ầ ố ộ n ?
b) Đánh giá ch t l ng h th ng ( Sai l ch tĩnh, đ v t l , th i gianấ ượ ệ ố ệ ộ ọ ố ờ
xác l p (2%), th i gian tăng t c)?ậ ờ ố
Câu 9: Thi t k khâu hi u ch nh s m pha d ng ph ng pháp QĐNSế ế ệ ỉ ớ ụ ươ
th a mãn đi u ki n POT < 10%, tỏ ề ệ qd < 0,5s (tiêu chu n 2%)?ẩ
R(s) C(s)
-
)1(
4
+ss
Gc(s)