Đ KI M TRA H C KÌ 2Ề Ể Ọ
Môn : Toán10
Đ 1ề
Câu 1(2 đi m): Gi i các b t ph ng trình sau:ể ả ấ ươ
1.
0
1
)43)(32( >
−
+−
x
xx
2.
65
2+− xx
2
+≤
x
Câu 2(2 đi m): Cho b ng phân b t n s ghép l p v k t qu đi m thiể ả ố ầ ố ớ ề ế ả ể
c a ủ45 h c sinh l p 10A nh sau:ọ ớ ư
Ghép l pớT n sầ ố
[ 0; 2)
[ 2; 4)
[ 4; 6)
[ 6; 8)
[ 8; 10]
2
6
10
17
10
C ngộ 45
1. L p b ng phân b t n su t ghép l p. V bi u đ t n su tậ ả ố ầ ấ ớ ẽ ể ồ ầ ấ
hình
c t.ộ
2. Tính đi m trung bình c a l p 10Aể ủ ớ
Câu 3(1 đi m): Ch ng minh r ng:ể ứ ằ
1cossin
cos2
cos1
1cossin
+−
=
−
−+
αα
α
α
αα
(
α
∀
đã tho mãn đi u ki n )ả ề ệ
Câu 4(4 đi m): Trong m t ph ng v i h tr c t a đ Oxy.ể ặ ẳ ớ ệ ụ ọ ộ
1) Cho
∆
ABC có A(1; 1), hai đ ng cao đi qua B và C ườ l nầ
l t ượ
có ph ng trình là (dươ 1): x - y + 5 = 0 và
(d2): 3x - 2y -16 = 0.
Vi t ph ng trình các c nh c a ế ươ ạ ủ
∆
ABC
2) Cho đ ng tròn (C) có ph ng trình:ườ ươ
x2 + y2 - 4x + 2y - 4 = 0
a. Xác đ nh tâm và bán kính c a đ ng tròn (C)ị ủ ườ
b. L p ph ng trình ti p tuy n v i đ ng tròn (C) bi t ậ ươ ế ế ớ ườ ế
ti p tuy n ế ế
4x - 3y -17 = 0
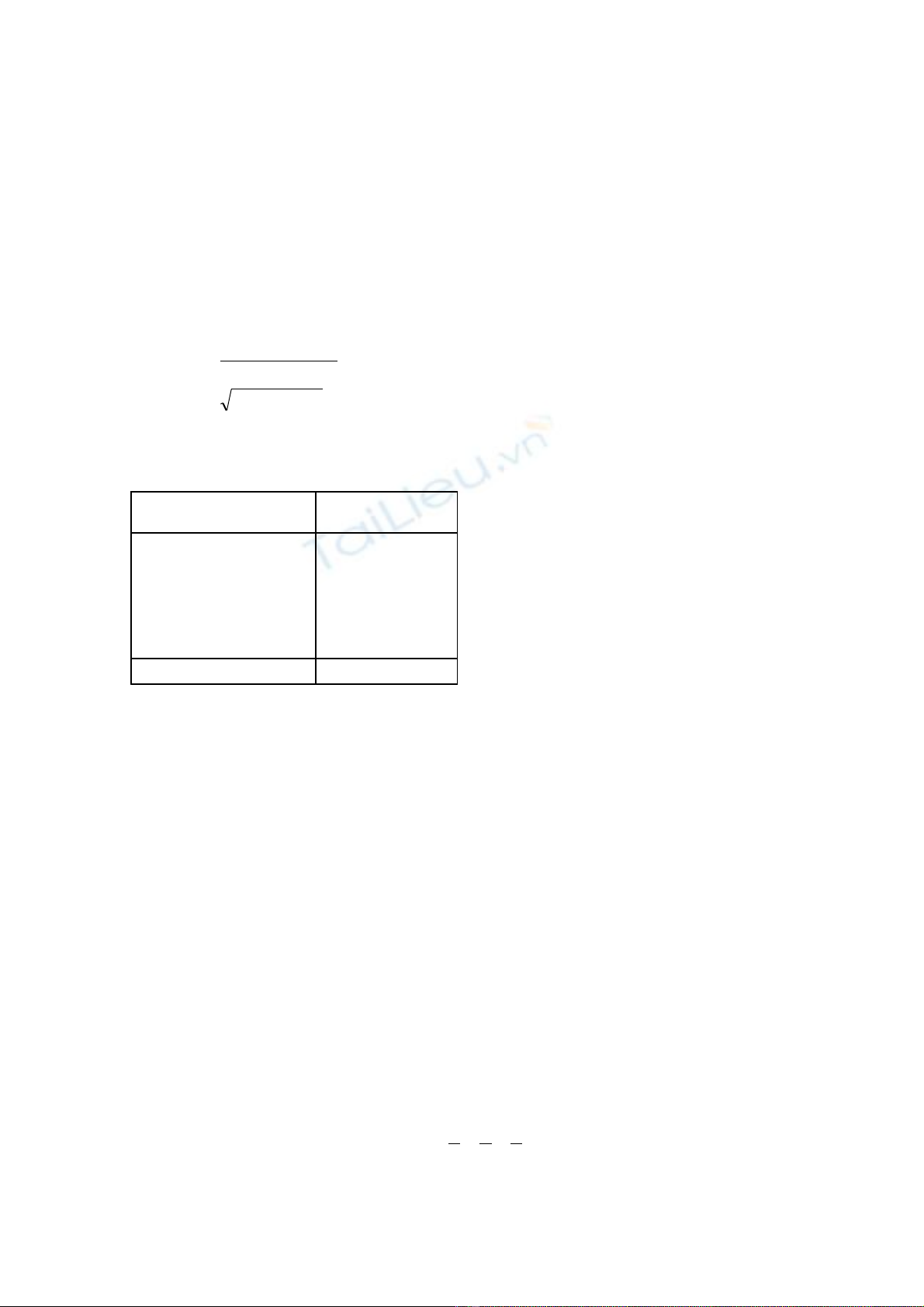
Câu 5 :(1 đi m ) Cho x, y, z > 0 và ể
4
111 =++ zyx
.
Ch ng minh r ng :ứ ằ
1
2
1
2
1
2
1≤
++
+
++
+
++ zyxzyxzyx
.
Đ ng th c x y ra khi nào?ẳ ứ ả
Đ KI M TRA H C KÌ 2Ề Ể Ọ
Môn : Toán10
Đ 2ề
Câu 1(2 đi m): Gi i các b t ph ng trình sau:ể ả ấ ươ
1.
0
1
)23)(43( >
−
+−
x
xx
2.
127
2+− xx
2
+≤
x
Câu 2(2 đi m): Cho b ng phân b t n s ghép l p v k t qu đi m thiể ả ố ầ ố ớ ề ế ả ể
c a ủ 45 h c sinh l p 10A nh sau:ọ ớ ư
1.L p b ng phân b t n su t ghép l p. V bi u đ t n su tậ ả ố ầ ấ ớ ẽ ể ồ ầ ấ
hình
c t.ộ
2. Tính đi m trung bình c a l p 10Aể ủ ớ
Câu 3(1 đi m): Ch ng minh r ng ể ứ ằ ∀ , ta có : ỏ
αααααα
cos.sin2)1cos)(sin1cos(sin =−+++
.
Câu 4(4 đi m): Trong m t ph ng v i h tr c t a đ Oxy.ể ặ ẳ ớ ệ ụ ọ ộ
1) Cho
∆
ABC có A(2; 6), hai đ ng cao đi qua B và C l n l tườ ầ ượ
có
ph ng trình là (dươ 1): x - 2y - 5 = 0 và (d2): x + 2y -5 = 0.
Vi t ph ng trình các c nh c a ế ươ ạ ủ
∆
ABC
2) Cho đ ng tròn (C) có ph ng trình:ườ ươ
x2 + y2 - 4x + 6y - 3 = 0
a. Xác đ nh tâm và bán kính c a đ ng tròn (C)ị ủ ườ
b. L p ph ng trình ti p tuy n v i đ ng tròn (C) bi t ậ ươ ế ế ớ ườ ế
ti p tuy n song song v i ế ế ớ
:)(d
4x + 3y -12 = 0.
Câu 5(1 đi m ): Cho x, y, z >ể0 và
4
111 =++ zyx
Ghép l pớ T n sầ ố
[ 0; 2)
[ 2; 4)
[ 4; 6)
[ 6; 8)
[ 8; 10 ]
3
5
11
16
10
C ngộ 45
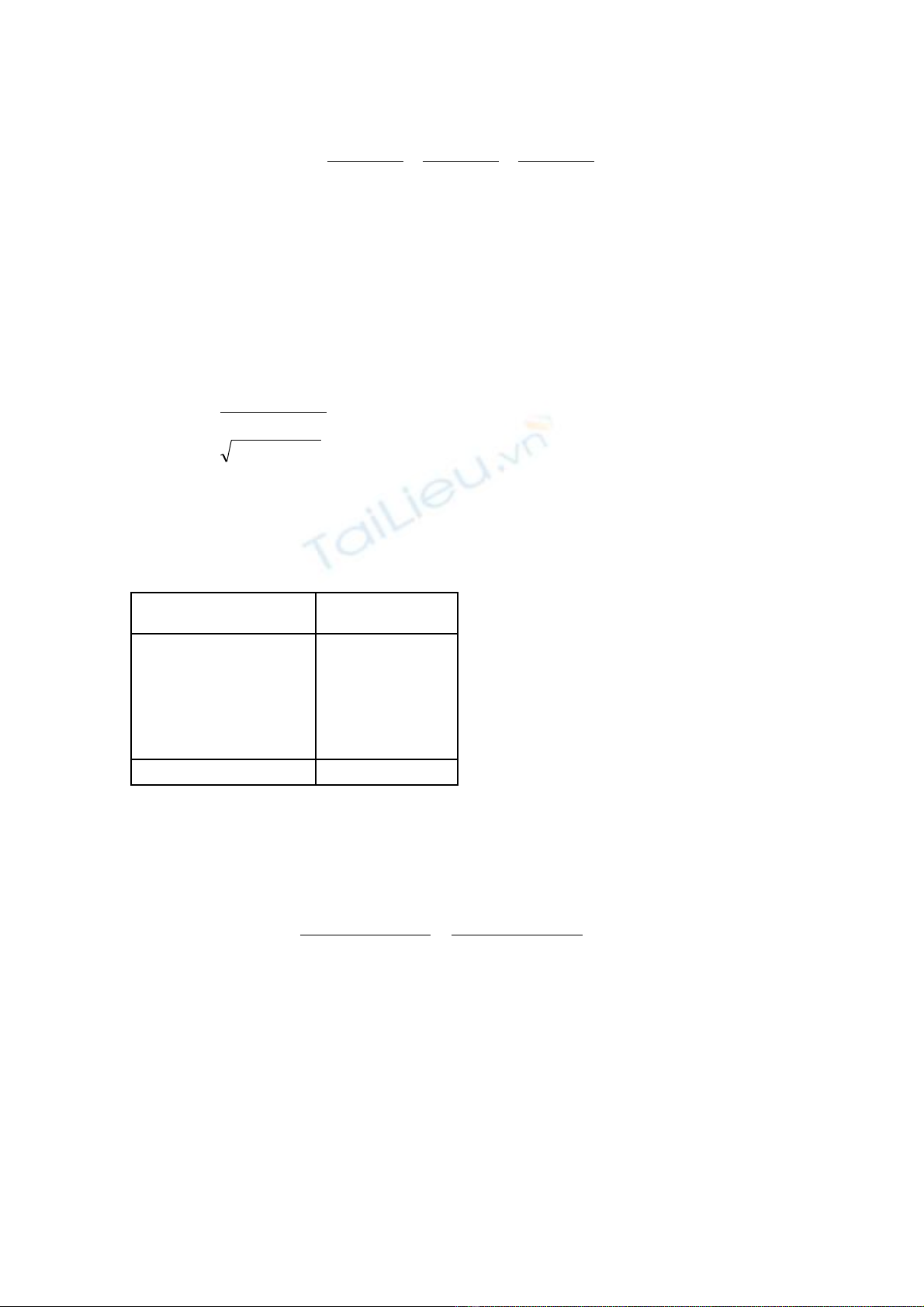
Ch ng minh r ng :ứ ằ
1
2
1
2
1
2
1≤
++
+
++
+
++ zyxzyxzyx
Đ ng th c x y ra khi nào?ẳ ứ ả
Đ KI M TRA H C KÌ 2Ề Ể Ọ
Môn : Toán10
Đ 3ề
Câu 1(2 đi m): Gi i các b t ph ng trình sau:ể ả ấ ươ
1.
0
5
)4)(12( ≥
−
−+
x
xx
2.
154 2++ xx
32
−<
x
Câu 2(2 đi m):ể
Cho b ng phân b t n s ghép l p v k t qu đi m thi c a 45ả ố ầ ố ớ ề ế ả ể ủ
h cọ
sinh l p 10A nh sau:ớ ư
Ghép l pớ T n sầ ố
[ 0; 2)
[ 2; 4)
[ 4; 6)
[ 6; 8)
[ 8; 10]
3
7
20
10
5
C ngộ45
1. L p b ng phân b t n su t ghép l p. V bi u đ t n su t ậ ả ố ầ ấ ớ ẽ ể ồ ầ ấ
hình c t.ộ
2. Tính đi m trung bình c a l p 10A.ể ủ ớ
Câu 3(1 đi m): Ch ng minh r ng ể ứ ằ
α
∀
đã tho mãn đi u ki n, ta có :ả ề ệ
1cos2sin
cos
sin4cos
1cos2sin
+−
=
−
−−
αα
α
αα
αα
Câu 4(4 đi m):Trong m t ph ng v i h tr c t a đ Oxy.ể ặ ẳ ớ ệ ụ ọ ộ
1)Cho
∆
ABC có A(3; 2), hai đ ng cao đi qua B và C l n l tườ ầ ượ
có
ph ng trình là (dươ 1): 4x – y – 3 = 0 và (d2): 2x + y – 1 = 0.
Vi t ph ng trình các c nh c a ế ươ ạ ủ
∆
ABC
2) Cho đ ng tròn (C) có ph ng trình:ườ ươ
x2 + y2 - 4x + 6y - 3= 0
a. Xác đ nh tâm và bán kính c a đ ng tròn (C)ị ủ ườ
b. L p ph ng trình ti p tuy n v i đ ng tròn (C) bi t ậ ươ ế ế ớ ườ ế
ti p tuy n // d : 6x – 8y + 5 = 0ế ế
Câu 5(1 đi m ) : Cho x, y, z > 0 và ể
4
111 =++ zyx
.
Ch ng minh r ng: ứ ằ
1
2
1
2
1
2
1≤
++
+
++
+
++ zyxzyxzyx
Đ ng th c x y ra khi nào?ẳ ứ ả
Đ KI M TRA H C KÌ 2Ề Ể Ọ
Môn : Toán10
Đ 4ề
Câu 1(2 đi m): Gi i các b t ph ng trình sau:ể ả ấ ươ
1.
0
51
)13)(2( <
−
+−
x
xx
2.
45
2++ xx
2
−≤
x
Câu 2(2 đi m): ể
Cho b ng phân b t n s ghép l p v k t qu đi m thi c a 45ả ố ầ ố ớ ề ế ả ể ủ
h c ọ
sinh l p 10A nh sau:ớ ư
Ghép l pớ T n sầ ố
[ 0; 2)
[ 2; 4)
[ 4; 6)
[ 6; 8)
[ 8; 10]
3
10
15
10
7
C ngộ45
1. L p b ng phân b t n su t ghép l p. V bi u đ t n su tậ ả ố ầ ấ ớ ẽ ể ồ ầ ấ
hình c t.ộ
2. Tính đi m trung bình c a l p 10A.ể ủ ớ
Câu 3(1 đi m): Ch ng minh r ng ể ứ ằ ∀ , ta có:ỏ
( sin + 2cos – 1)(sin + 2cos +1) = cos (cos +ỏ ỏ ỏ ỏ ỏ ỏ
4sin ) . Câu 4(4 đi m): Trong m t ph ng v i h tr c t a đ Oxy.ỏ ể ặ ẳ ớ ệ ụ ọ ộ
1)Cho
∆
ABC có A(1; 1), hai đ ng cao đi qua B và C l n l tườ ầ ượ
có
ph ng trình là (dươ 1): x – y – 5 = 0 và (d2): 2x + y – 1 = 0.
Vi t ph ng trình các c nh c a ế ươ ạ ủ ∆ABC .
2) Cho đ ng tròn (C) có ph ng trình:ườ ươ
x2 + y2 + 4x – 6y – 3 = 0 .
a. Xác đ nh tâm và bán kính c a đ ng tròn (C).ị ủ ườ
b. L p ph ng trình ti p tuy n v i đ ng tròn (C) bi t ậ ươ ế ế ớ ườ ế
ti p tuy n ế ế
8x + 6y – 5 = 0.
Câu 5(1 đi m ): Cho x, y, z > 0 và ể
4
111 =++ zyx
.
Ch ng minh r ng:ứ ằ
1
2
1
2
1
2
1≤
++
+
++
+
++ zyxzyxzyx
Đ ng th c x y ra khi nào?ẳ ứ ả
Đ KI M TRA H C KÌ 2Ề Ể Ọ
Môn : Toán10
Đ 5ề
Câu 1(2 đi m): Gi i các b t ph ng trình sau:ể ả ấ ươ
1. > 0 .
2. ≤ x + 3.
Câu 2(2 đi m): ể
Cho b ng phân b t n s ghép l p v k t qu đi m thi c a 45ả ố ầ ố ớ ề ế ả ể ủ
h c ọ
sinh l p 10A nh sau:ớ ư
Ghép l pớ T n sầ ố
[ 0; 2)
[ 2; 4)
[ 4; 6)
[ 6; 8)
[ 8; 10]
5
5
20
10
5
C ngộ45
1. L p b ng phân b t n su t ghép l p. V bi u đ t n su t ậ ả ố ầ ấ ớ ẽ ể ồ ầ ấ
hình c t.ộ
2. Tính đi m trung bình c a l p 10A.ể ủ ớ
Câu 3(1 đi m): Ch ng minh r ng ể ứ ằ ∀ , ta có :ỏ
(2 sin + cos – 1)(2sin + cos + 1) = sin (sin + 4sin ). ỏ ỏ ỏ ỏ ỏ ỏ ỏ
Câu 4(4 đi m): Trong m t ph ng v i h tr c t a đ Oxy.ể ặ ẳ ớ ệ ụ ọ ộ
1) Cho
∆
ABC có A(- 1; 3), hai đ ng cao đi qua B và C ườ l nầ
l t ượ