WWW.VNMATH.COM
Đ s 6ề ố
Đ ÔN T P H C KÌ 2 – Năm h c Ề Ậ Ọ ọ
Môn TOÁN L p 10ớ
Th i gian làm bài 90 phútờ
Câu 1:
1) Gi i các b t ph ng trình sau: ả ấ ươ
a)
x x5 1 3 1− ≤ +
b)
x x
x x
2
2
3 2 5 0
8 15
− − + ≥
− +
2) Cho y = (x + 3)(5 – 2x), –3 ≤ x ≤
5
2
. Đ nh ịx đ ểy đ t giá tr l n nh t.ạ ị ớ ấ
Câu 2: Cho ph ng trình: ươ
x x m m
2 2
2 8 15 0− + + − + =
a) Ch ng minh ph ng trình luôn có nghi mứ ươ ệ
b) Tìm m đ ph ng trình có 2 nghi m trái d uể ươ ệ ấ
Câu 3 : Trong h tr c t a đ Oệ ụ ọ ộ xy, cho đ ng tròn (C ): ườ
x y
2 2
( 1) ( 2) 8− + − =
a) Xác đ nh tâm I và bán kính R c a (C )ị ủ
b) Vi t ph ng trình đ ng th ng ế ươ ườ ẳ ∆ qua I, song song v i đ ng th ng d: ớ ườ ẳ x – y – 1 = 0
c) Vi t ph ng trình ti p tuy n c a (C ) vuông góc v i ế ươ ế ế ủ ớ ∆
Câu 4:
a) Cho cos
α
– sin
α
= 0,2. Tính
3 3
cos sin
α α
−
?
b) Cho
a b 3
π
− =
. Tính giá tr bi u th c ị ể ứ
.
Câu 5: Ti n lãi (nghìn đ ng) trong 30 ngày đ c kh o sát m t qu y bán báo.ề ồ ượ ả ở ộ ầ
81 37 74 65 31 63 58 82 67 77 63 46 30 53 73
51 44 52 92 93 53 85 77 47 42 57 57 85 55 64
a) Hãy l p b ng phân b t n s và t n su t theo các l p nh sau:ậ ả ố ầ ố ầ ấ ớ ư
[29.5; 40.5), [40.5; 51.5), [51.5; 62.5), [62.5; 73.5), [73.5; 84.5), [84.5; 95.5]
b) Tính s trung bình c ng, ph ng sai, đ l ch chu n ?ố ộ ươ ộ ệ ẩ
--------------------H t-------------------ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
WWW.VNMATH.COM
Đ s 6ề ố
ĐÁP ÁN Đ ÔN T P H C KÌ 2 – Năm h c Ề Ậ Ọ ọ
Môn TOÁN L p 10ớ
Th i gian làm bài 90 phútờ
Câu 1:
1) Gi i các b t ph ng trình sau: ả ấ ươ
a)
x x x x x
2
5 1 3 1 16 16 0 [0;1]− ≤ + ⇔ − ≤ ⇔ ∈
b)
x x x x x
x x
x x
2
2
3 2 5 ( 1)(3 5) 5
0 0 ;1 (3;5)
( 3)( 5) 3
8 15
− − + − − + −
≥ ⇔ ≥ ⇔ ∈ ∪
− −
− +
2) Cho y = (x + 3)(5 – 2x), –3 ≤ x ≤
5
2
. Đ nh ịx đ ểy đ t giá tr l n nh t.ạ ị ớ ấ
Vì –3 ≤ x ≤
5
2
nên
x x3 0, 5 2 0+ ≥ − ≥
.
Ta có:
x x2( 3) (5 2 ) 11+ + − =
(không đ i) nên ổ
y x x2 2( 3)(5 2 )= + −
đ t GTLN khi ạ
x x2( 3) 5 2+ = −
⇔
x1
4
= −
.
V y ậy = (x + 3)(5 – 2x) đ t GTLN khi ạ
x1
4
= −
. Khi đó
y121
max 8
=
Câu 2: Cho ph ng trình: ươ
x x m m
2 2
2 8 15 0− + + − + =
a) Ch ng minh ph ng trình luôn có nghi mứ ươ ệ
PT ⇔
x x m m
2 2
2 8 15 0− − + − =
có
m m m m R
2 2
1 8 15 ( 2) 0,
∆
′= + − + = − ≥ ∀ ∈
⇒ PT luôn luôn có nghi m v i m i s th c ệ ớ ọ ố ự m.
b) Tìm m đ ph ng trình có 2 nghi m trái d uể ươ ệ ấ
PT có hai nghi m trái d u ệ ấ ⇔ ac < 0 ⇔
m
m m m
23
1( 8 15) 0 5
<
− + − < ⇔ >
Câu 3 : Trong h tr c t a đ Oệ ụ ọ ộ xy, cho đ ng tròn (C ): ườ
x y
2 2
( 1) ( 2) 8− + − =
a) Tâm I(1; 2) , bán kính R =
2 2
b) Vi t ph ng trình đ ng th ng ế ươ ườ ẳ ∆ qua I, song song v i đ ng th ng d: ớ ườ ẳ x – y – 1 = 0
• ∆// d nên ph ng trình ươ ∆ có d ng ạ
x y C 0− + =
(C ≠ –1)
• ∆ đi qua I nên có
C C1 2 0 1− + = ⇔ =
⇒ PT
x y: 1 0
∆
− + =
c) Vi t ph ng trình ti p tuy n c a (C ) vuông góc v i ế ươ ế ế ủ ớ ∆
•Ti p tuy n ế ế
1
∆
vuông góc v i ớ∆ nên PTTT có d ng ạ
x y D 0+ + =
và
DD
d I R D D
2
12 2
1 2 7
( , ) 8 ( 3) 16 1
1 1
∆
+ + = −
= ⇔ = ⇔ + = ⇔ =
+
V y PT các ti p tuy n c n tìm: ậ ế ế ầ
x y x y1 0, 7 0+ + = + − =
.
Câu 4:
a) Cho cos
α
– sin
α
= 0,2. Tính
3 3
cos sin
α α
−
?
Ta có:
cos sin 0,2 1 2sin cos 0,04 sin cos 0,48
α α α α α α
− = ⇔ − = ⇔ =
Do đó:
in
3 3
cos sin (cos s )(1 sin cos ) 0,2(1 0,48) 0,296
α α α α α α
− = − + = + =
b) Cho
a b 3
π
− =
. Tính giá tr bi u th c ị ể ứ
.
A a b a b a b a b
2 2
(cos cos ) (sin sin ) 2 2(cos cos sin sin )= + + + = + +
2
a b2 2cos( ) 2 2cos 3
3
π
= + − = + =
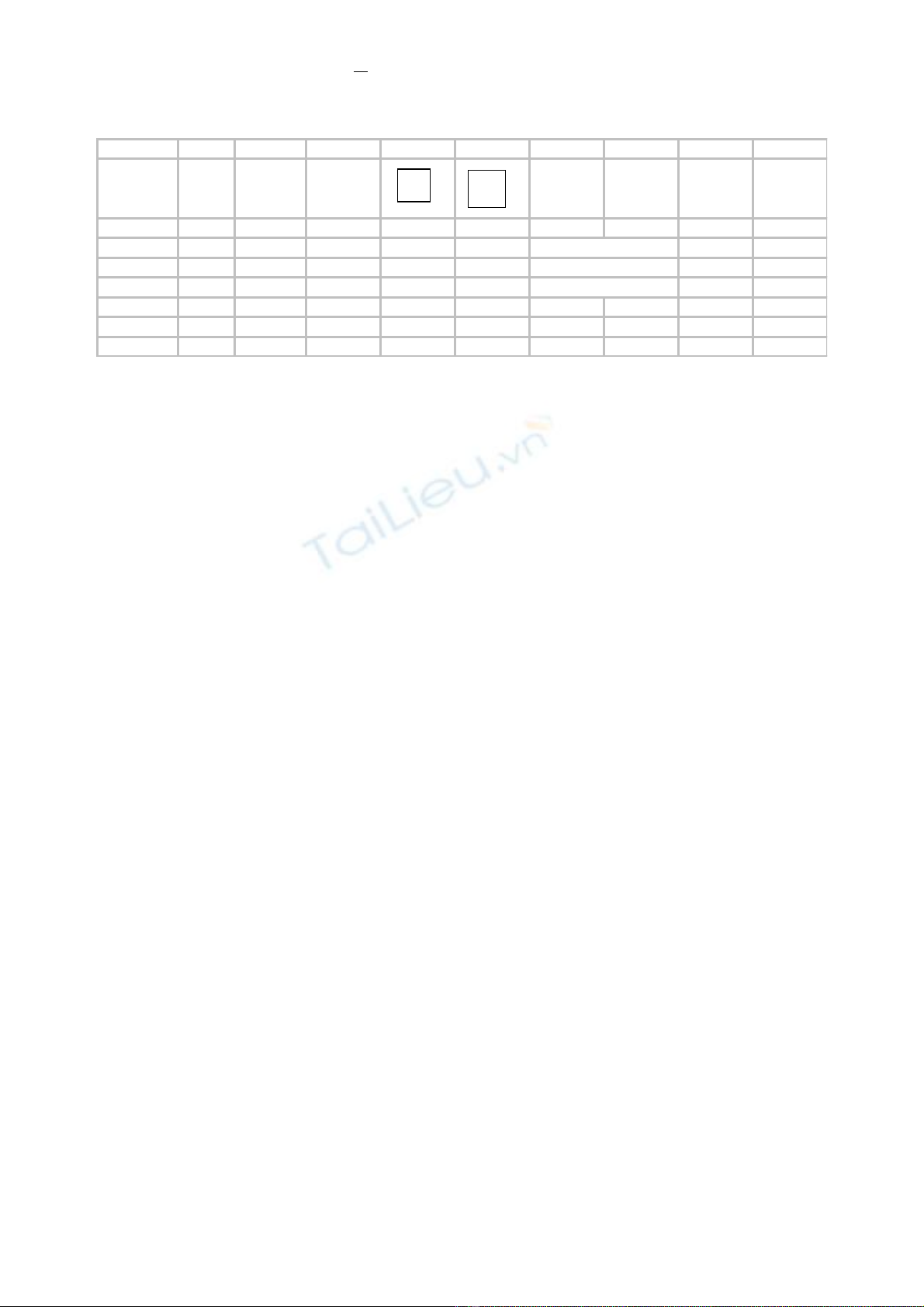
Câu 5:
L pớ
ti n lãiề
T n sầ ố
ni
T n su tầ ấ
fi
Giá trị
đ i di nạ ệ
ci
[29,5;40,5) 3 10% 35 105 3675
[40,5;51,5) 5 17% 46 230 10580 S trung bình c ng:ố ộ 63,23
[51,5;62,5) 7 23% 57 399 22743 Ph ng sai:ươ 279,78
[62,5;73,5) 6 20% 68 408 27744 Đ l ch chu n:ộ ệ ẩ 16,73
[73,5;84,5) 5 17% 79 395 31205
[84,5;95,5] 4 13% 90 360 32400
N 30 100% 1897 128347
i i
n c
i i
n c
2
===================
3