Đ THI CH N HSG L P 8 (l n 2)Ề Ọ Ớ ầ
Năm h c 2009 - 2010ọ
Bài 1: Cho bi u th c M =ể ứ
+
+
−
+
−2
1
36
6
4
3
2
xx
xx
x
:
+
−
+− 2
10
2
2
x
x
x
a) Rút g n Mọ
b)Tính giá tr c a M khi ị ủ
x
=
2
1
Bài 2: Cho bi u th c: A = ( bể ứ 2 + c2 - a2)2 - 4b2c2
a) Phân tích bi u th c A thành nhân t .ể ứ ử
b) Ch ng minh r ng : N u a, b, c là đ dài các c nh c a m t tam giác thì A <ứ ằ ế ộ ạ ủ ộ
0.
Bài 3:
a)Tìm giá tr nh nh t c a bi u th c sau :ị ỏ ấ ủ ể ứ
A = x2 - 2xy + 2y2 - 4y + 5
b)Tìm giá tr l n nh t c a bi u th c sau :ị ớ ấ ủ ể ứ
B =
1
)1(3
23 +++
+
xxx
x
Bài 4:
Cho hình bình hành ABCD . V i AB = a ; AD = b. T đ nh A , k m t đ ngớ ừ ỉ ẻ ộ ườ
th ng a b t kỳ c t đ ng chéo BD t i E, c t c nh BC t i F và c t tia DC t iẳ ấ ắ ườ ạ ắ ạ ạ ắ ạ
G.
a) Ch ng minh: AEứ2 =EF.EG
b). Ch ng minh r ng khi đ ng th ng a quay quanh A thay đ i thì tíchứ ằ ườ ẳ ổ
BF.DG không đ i.ổ
Bài 5:
Ch ng minh r ng n u ứ ằ ế
)1()1(
22
xzy
xzy
yzx
yzx
−
−
=
−
−
V i x ớ
≠
y ; xyz
≠
0 ; yz
≠
1 ; xz
≠
1.
Thì : xy + xz + yz = xyz ( x + y + z)
HD:
Bài 1:
a) Rút g n Mọ
M=
+
+
−
+
−2
1
36
6
4
3
2
xx
xx
x
:
+
−
+− 2
10
2
2
x
x
x
=
:
2
6
+x
M =
6
2
.
)2)(2(
6+
+−
−x
xx
=
x−2
1
b)Tính giá tr c a M khi ị ủ
x
=
2
1
x
=
2
1
⇔
x =
2
1
ho c x = -ặ
2
1
V i x = ớ
2
1
ta có : M =
2
1
2
1
−
=
2
3
1
=
3
2
V i x = - ớ
2
1
ta có : M =
2
1
2
1
+
=
2
5
1
=
5
2
Bài 2a) Phân tích bi u th c A thành nhân t .ể ứ ử
Ta có : A = ( b2 + c2 - a2)2 - 4b2c2 = ( b2 + c2 - a2)2 - (2bc)2 = ( b2 + c2 - a2-2bc)( b2
+ c2 - a2+2bc) = (b+c -a) (b+c+a) (b-c-a) (b-c+a)
b) Ch ng minh r ng : N u a, b, c là đ dài các c nh c a m t tam giác thì A <ứ ằ ế ộ ạ ủ ộ
0.
Ta có: (b+c -a) >0 ( BĐT trong tam giác)
(b+c +a) >0 ( BĐT trong tam giác)
(b-c -a) <0 ( BĐT trong tam giác)
(b+c -a) >0 ( BĐT trong tam giác)
V y A< 0ậ
Bài 3:
a)
Ta có : A = x2 - 2xy + y2 +y2 - 4y +4 + 1
= (x-y)2 + (y - 2)2 + 1
Do (x-y)2
≥
0 ; (y - 2)2
≥
0
Nên A= (x-y)2 + (y - 2)2 + 1
≥
1
D u ''='' xãy ra ấ
⇔
x = y và y = 2
V y GTNN c a A là 1ậ ủ
⇔
x = y =2
b) B =
1
)1(3
23 +++
+
xxx
x
=
1)1(
)1(3
2
+++
+
xxx
x
=
)1)(1(
)1(3
2++
+
xx
x
=
1
3
2+x
Do x2 +1>0 nên B =
1
3
2
+x
≤
3
D u ''='' xãy ra ấ
⇔
x = 0
V y GTLN c a B là 3ậ ủ
⇔
x = 0
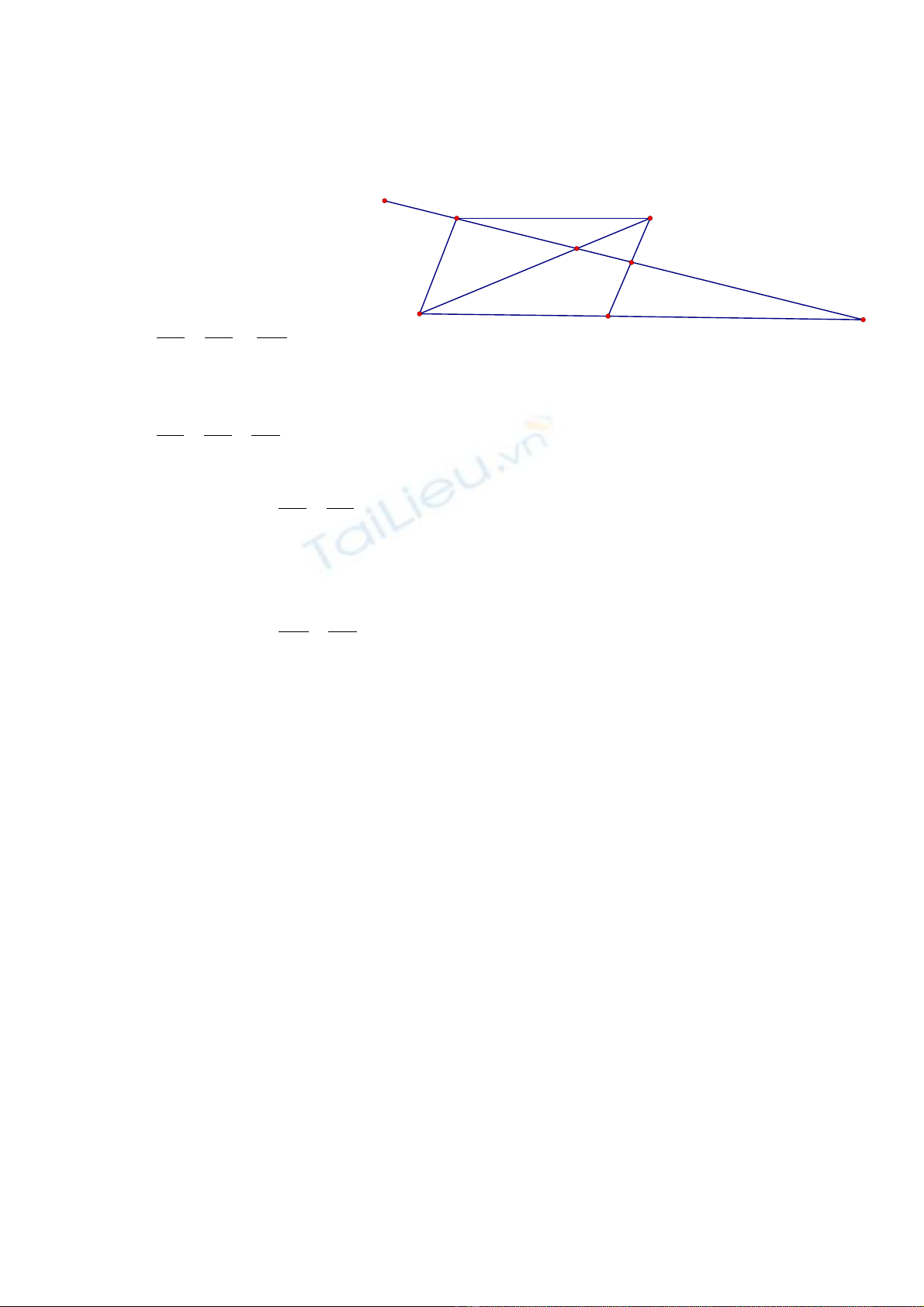
Bài 4:
a)
Do AB//CD nên ta có:
ED
EB
EG
EA =
=
DG
AB
(1)
Do BF//AD nên ta có:
ED
EB
EA
EF =
=
FB
AD
(2)
T (1) và (2) ừ
⇒
EA
EF
EG
EA =
Hay AE2 = EF. EG
b). Ch ng minh r ng khi đ ng th ng a quay quanh A thay đ i thì tíchứ ằ ườ ẳ ổ
BF.DG không đ i.ổ
T (1) và (2) ừ
⇒
AD
FB
DG
AB =
Hay BF.DG = AB.AD = ab (không đ i)ổ
Bài 5:
T GT ừ
⇒
(x2 -yz)y(1-xz) = x(1- yz)(y2 - xz)
⇔
x2y- x3yz-y2z+xy2z2 = xy2 -x2z - xy3z +x2yz2
⇔
x2y- x3yz - y2z+ xy2z2 - xy2 +x2z + xy3z - x2yz2 = 0
⇔
xy(x-y) +xyz(yz +y2- xz - x2)+z(x2 - y2) = 0
⇔
xy(x-y) - xyz(x -y)(x + y +z)+z(x - y)(x+y) = 0
⇔
(x -y)
[ ]
yzxzzyxxyzxy ++++− )(
= 0
Do x - y
≠
0 nên xy + xz + yz - xyz ( x + y + z) = 0
Hay xy + xz + yz = xyz ( x + y + z) (đpcm)
E
F
A
B
D
C
G