KÌ THI CH N H C SINH GI I L P 8 C PỌ Ọ Ỏ Ớ Ấ
HUY NỆ
NĂM H C 2009-2010Ọ
Môn : Toán
Th i gian : 150 phút( Không k th i gian giao đ )ờ ể ờ ề
Bài 1: Ch ng minh r ng: 11ứ ằ 10 - 1 chia h t cho 100.ế
Bài 2: Phân tích đa th c thành nhân t : P = xứ ử 2( y - z ) + y2( z - x ) + z2( x - y )
Bài 3: Cho bi u th c: Q = 1 + ể ứ
xxx
xx
x
xxx
x
+−
−
+
−
−−
−
+
+
23
23
23
2
:
1
2
1
1
1
1
a- Rút g n Q.ọ
b- Tính giá tr c a Q bi t: ị ủ ế
4
5
4
3=−x
c-Tìm giá tr nguyên c a x đ Q có giá tr nguyên.ị ủ ể ị
Bài 4: Tìm giá tr c a m đ cho ph ng trình: 6x - 5m = 3 + 3mx có nghi m s g p ba nghi m sị ủ ể ươ ệ ố ấ ệ ố
c a ph ng trình: ( x + 1)( x - 1) - ( x + 2)ủ ươ 2 = 3
Bài 5: Tìm t t c các c p s nguyên ( x; y) tho mãn ph ng trình: xấ ả ặ ố ả ươ 2 -25 = y( y+6)
Bài 6: Cho hình vuông ABCD, M là đi m b t kì trên c nh BC. Trong n a m t ph ng b AB ch a Cể ấ ạ ử ặ ẳ ờ ứ
d ng hình vuông AMHN.Qua M d ng đ ng th ng d song song v i ự ự ườ ẳ ớ AB, d c t AH E, c t DC F.ắ ở ắ ở
a- Ch ng minh r ng: BM = ND.ứ ằ
b-Ch ng minh r ng: N; D; C th ng hàng.ứ ằ ẳ
c-EMFN là hình gì?
d-Ch ng minh: DF + BM = FM và chu vi tam giác MFC không đ i khi M thay đ i v trí trên BC. ứ ổ ổ ị
...................................H t ...........................................ế
(Đ thi g m 01 trang)ề ồ
*Yêu c u: H c sinh không gi i toán b ng máy tínhầ ọ ả ằ
H NG D N CH M Đ THI H C SINH GI I L P 8 C P HUY NƯỚ Ẫ Ấ Ề Ọ Ỏ Ớ Ấ Ệ
MÔN: TOÁN 8
(H ng d n ch m g m: 03 trang)ướ ẫ ấ ồ
Câu N i dungộBi u đi mể ể
Bài 1 1110 - 1 = ( 11 -1 )(
1111111 89 ++⋅⋅⋅++
)
= 10(
1111111 89 ++⋅⋅⋅++
)
Vì 10
10
và (
1111111 89 ++⋅⋅⋅++
) có ch s t n cùng ( hàng đ n v ) b ng 0ữ ố ậ ơ ị ằ
Nên: (
1111111 89 ++⋅⋅⋅++
) chia h t cho 10ế
V y: 11ậ10 - 1 chia h t cho 10.ế
0.5
0.5
0.25
0.25
0.25
0.25
Bài 2: x2( y - z ) + y2( z - x ) + z2( x - y )
= x
2
( )
yzxzxyzyzy 2222 −+−+−
=
( ) ( )
( )
( )
( )
( ) ( ) ( )
[ ]
( )( )( )
zxyxzy
yxzyxxzy
xzxyyzxzy
zyxzyyzzyx
−−−=
−−−−=
−−+−=
−−−+−
2
222
0.5
0.5
0.25
0.25
0.25
0.25
Bài 3 a) Q = 1 +
xxx
xx
x
xxx
x
+−
−
+
−
−−
−
+
+
23
23
23
2
:
1
2
1
1
1
1
=
( )
( )
( )
( )
( )
( )
( )
2
1
11
22
1
2
1
11
42
1
2
2
2
2
2
−
+−
⋅
+−+
−−
+=
−
+−
⋅
+−−
+−
+=
xx
xx
xxx
xx
xx
xx
xxx
xx
(Đi u ki n: xề ệ
≠
0;-1; 2)
1
1
1
2
1
+
−
=
+
−
+=
x
x
x
−=
=
⇒
=−
2
1
2
4
5
4
3
x
x
x
( Lo i)ạ
V i xớ =
3
2
1−=⇒
−Q
c) Q
Z∈
v i ớ
{ }
1;2;3 −−∈x
1.0
1.0
1.0
0.25
0.25
0.25
0.25
0.25
0.75
Bài 4 ( x + 1)( x - 1) - ( x + 2)2 = 3 ( 1)
2
84
3441 22
−=⇔
=−⇔
=−−−−⇔
x
x
xxx
Đ ph ng trình 6x - 5m = 3 + 3mx có nghi m g p ba l n nghi m c aể ươ ệ ấ ầ ệ ủ
ph ng trình ( x + 1)( x - 1) - ( x + 2)ươ 2 = 3 hay x =-6
b)
Ta có: 6(-6) - 5m = 3 +3m(-6)
3
3913
39185
=⇔
=⇔
=+−⇔
m
m
mm
V y: V i m = 3 thì ph ng trình 6x - 5m = 3 + 3mx có nghi m s g p baậ ớ ươ ệ ố ấ
nghi m s c a ph ng trình: ( x + 1)( x - 1) - ( x + 2)ệ ố ủ ươ 2 = 3
Bài 5 x2 -25 = y( y+6)
( )( ) ( )( ) ( )( ) ( )( )
161;82;4433
16)3( 22
±±±±±±=−−++⇔
=+−⇔
yxyx
yx
Suy ra: x-y 7 -1 5 1 11 -5 4 2 19 -13
x+y 1 -7 5 -11 -1 -5 13 -19 -2 -4
V y: các c p s nguyên ph i tìm làậ ặ ố ả :
( ) ( ) ( ) ( ) ( ) ( )
0;5;6;5;6;5;0;5;3;4;3;4 −−−−−−−
Bài 6 a) ABCD là hình vuông ( gt)
⇒
A1 + MAD = 900 ( gt) (1)
Vì AMHN là hình vuông ( gt)
A2 + MAD = 900 (2)
T (1) và (2) suy ra: Aừ1 = A2
Ta có:
AMBAND
∆=Λ
( c.g.c)
B = D1 = 900 và BM= ND
b) ABCD là hình vuông =>D2 = 900
D1 + D2 = NDC
900 + 900 = NDC
NDC = 1800
N; D; C th ng hàngẳ
c) G i O là giao đi m c a hai đ ng chéo AH và MN c a hình vuông AMHNọ ể ủ ườ ủ
O là tâm đ i x ng c a hình vuông AMHNố ứ ủ
AH là đ ng trung tr c c a đo n MN, mà E;F ườ ự ủ ạ
∈
AH
EN = EM và FM = FN (3)
Tam giác vuông EOM = tam giác vuông FON ( OM= ON; N1=M3)
O1 = O 2
EM = NF (4)
T (3) và (4)ừ
EM=NE=NF=FM
MENF là hinh thoi (5)
d) T (5) suy ra: FM =ừ FN = FD +DN
Mà DN = MB ( cmt)
MF=DF+BM
G i chu vi tam giác MCF là p và c nh hình vuông ABCD là aọ ạ
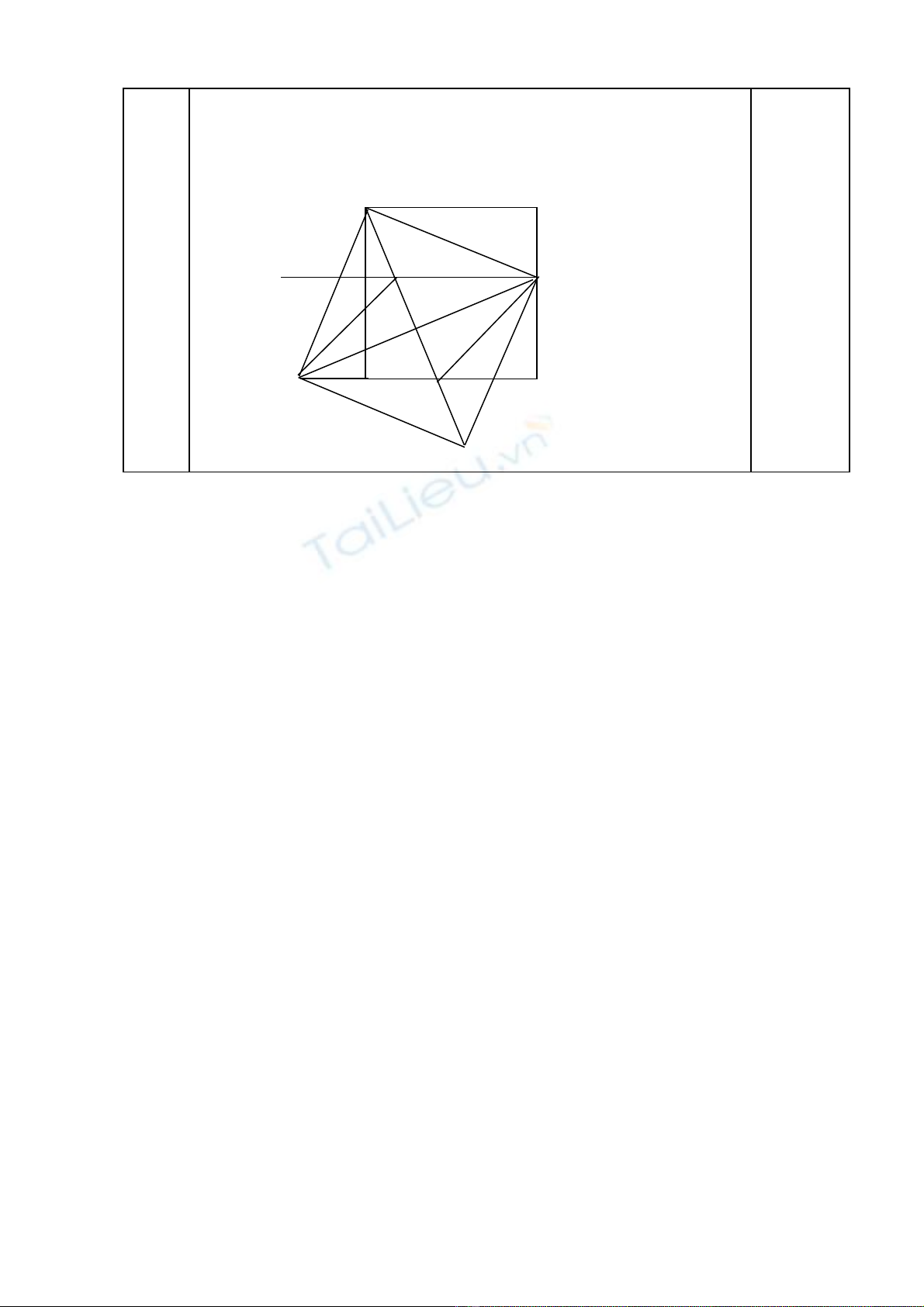
P = MC + CF + MF = MC +CF +BM + DF (Vì MF = DF+MB)
= (MC + MB) + ( CF + FD) = BC + CD = a + a = 2a
Hình vuông ABCD cho tr c ướ
a không đ i ổ
p không đ iổ
N D F C
M
A
d
H
O
E
B
1
3
2
2
12
1