Câu 1: Phân tích thành nhân tử: a, a8 + a4 +1 b, a10 + a5 +1
Câu 2: a, Cho a+b+c = 0, Tính giá trị của biểu thức:
A =
2 2 2
1
b c a
+
2 2 2
1
c a b
+
2 2 2
1
a b c
b, Cho biểu thức: M = 2
2 15
x
x x
+ Rút gọn M + Tìm x
Z để M đạt giá trị nguyên.
Câu 3: a, Cho abc = 1 và a3 > 36, CMR:
2
3
a
+ b2 + c2 > ab + bc + ca
b, CMR: a2 + b2 +1
ab + a + b
Câu 4: a, Tìm giá trị nhỏ nhất của A = 2x2 + 2xy + y2 - 2x + 2y +1
b, Cho a+b+c= 1, Tìm giá trị nhỏ nhất P = a3 + b3 + c3 + a2(b+c) + b2(c+a) +
c2(a+b)
Câu 5:
a, Tìm x,y,x
Z biết: x2 + 2y2 + z2 - 2xy – 2y + 2z +2 = 0
b, Tìm nghiệm nguyên của PT: 6x + 15y + 10z = 3
Câu 6: Cho
ABC
V. H là trực tâm, đường thẳng vuông góc với AB tại B, với AC tại
C cắt nhau tại D. a, CMR: Tứ giác BDCH là hình bình hành
b, Nhận xét mối quan hệ giữa góc
µ
A
và
µ
D
của tứ giác ABDC.
ĐỀ 2
Câu 1: a. Rút gọn biểu thức:
A= (2+1)(22+1)(24+1).......( 2256 + 1) + 1
b. Nếu x2=y2 + z2
Chứng minh rằng: (5x – 3y + 4z)( 5x –3y –4z) = (3x –5y)2
Câu 2: a. Cho 0
c
z
b
y
a
x
(1) và 2
z
c
y
b
x
a (2)
Tính giá trị của biểu thức A= 0
2
2
2
2
2
2
c
z
b
y
a
x
b. Tính : B = 222222222
b
a
c
ca
a
c
b
bc
c
b
a
ab
Câu 3: Tìm x , biết :
3
1988
19
1997
10
2006
1·
xxx (1)
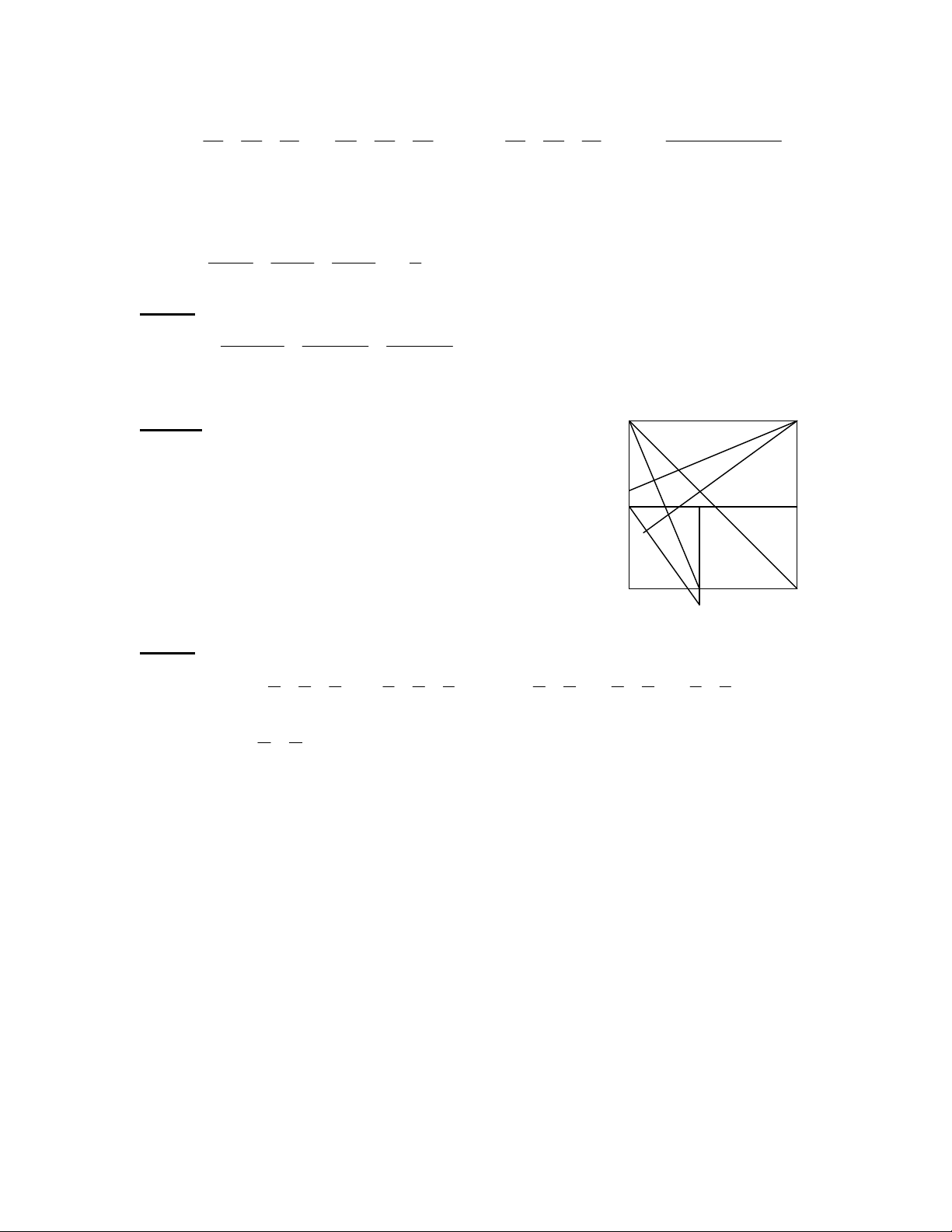
Câu 4: Cho hình vuông ABCD, M đương chéo AC. Gọi E,F theo thứ tự là hình
chiếu của M trên AD, CD. Chứng minh rằng:
a.BM EF
b. Các đường thẳng BM, EF, CE đồng quy.
Câu 5: Cho a,b, c, là các số dương. Tìm giá trị nhỏ nhất của
P= (a+ b+ c) (
c
b
a
111 ).
ĐÁP ÁN
Câu 1: a. ( 1,25 điểm) Ta có:
A= (2-1) (2+1) (22+1) ........ + 1
= (22-1)(22+1) ......... (2256+1)
= (24-1) (24+ 1) ......... (2256+1)
................
= [(2256)2 –1] + 1
= 2512
b, . ( 1 điểm) Ta có:
(5x – 3y + 4z)( 5x –3y –4z) = (5x – 3y )2 –16z2= 25x2 –30xy + 9y2 –16 z2 (*)
Vì x2=y2 + z2 (*) = 25x2 –30xy + 9y2 –16 (x2 –y2) = (3x –5y)2
Câu 2: . ( 1,25 điểm) a. Từ (1) bcx +acy + abz =0
Từ (2)
02
2
2
2
2
2
2
yz
bc
xz
ac
xy
ab
c
z
b
y
a
x 424
2
2
2
2
2
2
xyz
bcxacyabz
c
z
b
y
a
x
b. . ( 1,25 điểm) Từ a + b + c = 0 a + b = - c a2 + b2 –c2 = - 2ab
Tương tự b2 + c2 – a2 = - 2bc; c2+a2-b2 = -2ac
B =
2
3
2
2
2
ca
ca
bc
bc
ab
ab
Câu 3: . ( 1,25 điểm)
(1) 0
1988
2007
1997
2007
2006
2007·
xxx
x= 2007 A
Câu 4: a. ( 1,25 điểm) Gọi K là giao điểm CB với EM; B
H là giao điểm của EF và BM
EMB =BKM ( gcg)
Góc MFE =KMB BH EF E M K
b. ( 1,25 điểm) ADF = BAE (cgc) AF BE H
Tương tự: CE BF BM; AF; CE
là các đường cao của BEF đpcm
Câu 5: ( 1,5 điểm) Ta có: D F C
P = 1 +
b
c
c
b
a
c
c
a
a
b
b
a
b
c
a
c
c
b
a
b
c
a
b
a311
Mặt khác 2
x
y
y
x với mọi x, y dương. P 3+2+2+2 =9
Vậy P min = 9 khi a=b=c.
---------------------------------------
ĐỀ 3
Bài 1 (3đ):
1) Phân tích các đa thức sau thành nhân tử:
a) x2 + 7x + 12
b) a10 + a5 + 1
2) Giải phương trình:
2 4 6 8
98 96 94 92
x x x x
Bài 2 (2đ):
Tìm giá trị nguyên của x để biểu thức 2
2 3 3
2 1
x x
P
x
có giá trị nguyên
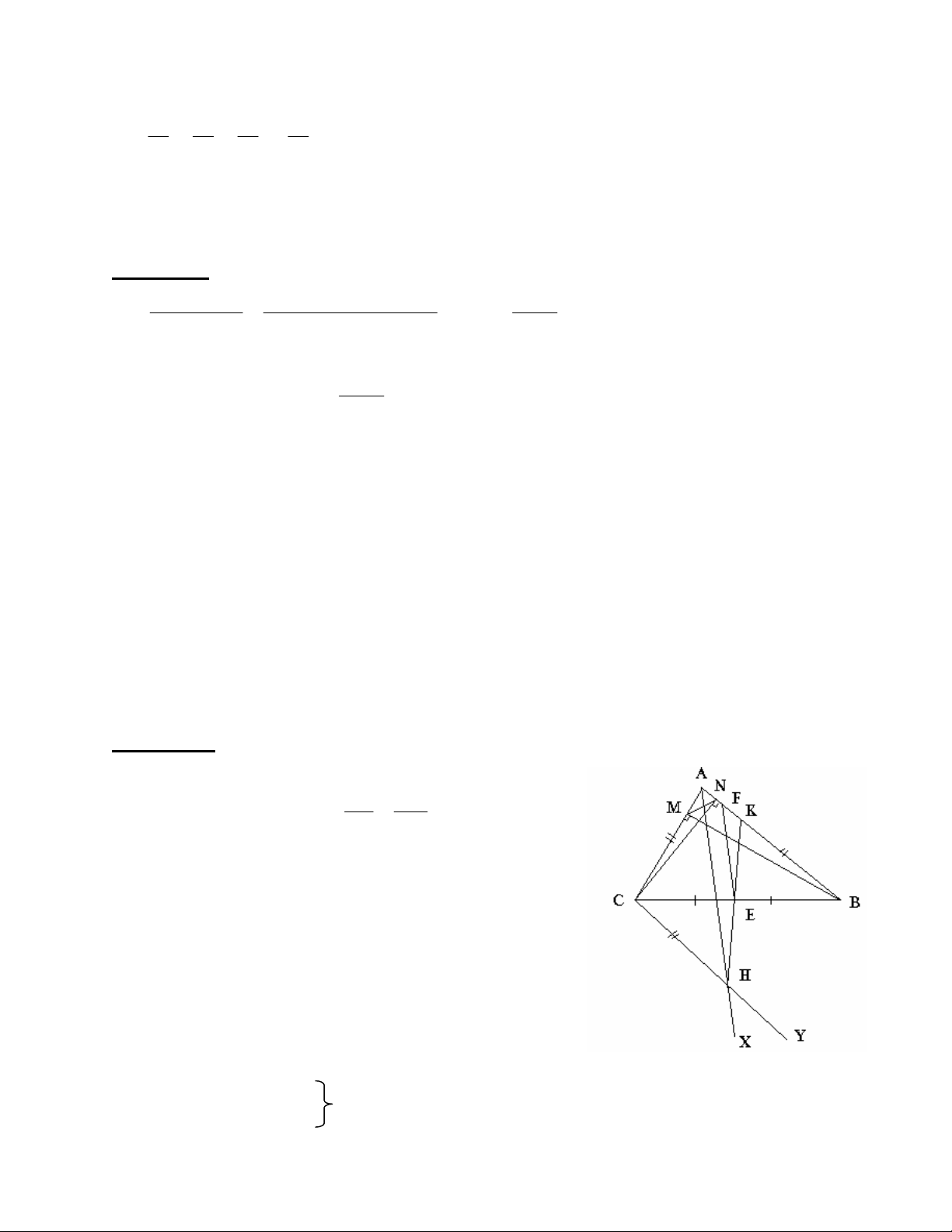
Bài 3 (4đ): Cho tam giác ABC ( AB > AC )
1) Kẻ đường cao BM; CN của tam giác. Chứng minh rằng:
a)
ABM
đồng dạng
ACN
b) góc AMN bằng góc ABC
2) Trên cạnh AB lấy điểm K sao cho BK = AC. Gọi E là trung điểm của BC;
F là trung điểm của AK.
Chứng minh rằng: EF song song với tia phân giác Ax của góc BAC.
Bài 4 (1đ):
Tìm giá trị nhỏ nhất của biểu thức:
2
2
2007
20072
x
xx
A
, ( x khác 0)
ĐÁP ÁN
Bài 1 (3đ):
1) a) x2 + 7x + 12 = (x+3)(x+4) (1đ)
b) a10 + a5 + 1 = (a10 + a9 + a8 ) - (a9 + a8 + a7 ) + (a7 + a6 + a5 ) - (a6 + a5 + a4
) + (a5 + a4 + a3 ) - (a3 + a2 + a ) + (a2 + a + 1 ) = (a2 + a + 1 )( a8 - a7 + a5 - a4 + +
a3 - a+ 1 ) (1đ)
2)
92
8
94
6
96
4
98
2
xxxx
(
98
2
x+1) + (
96
4
x + 1) = (
94
6
x + 1) + (
92
8
x + 1) (0,5đ)
( x + 100 )(
98
1 +
96
1 -
94
1 -
92
1) = 0 (0,25đ)
Vì:
98
1 +
96
1 -
94
1 -
92
1
0
Do đó : x + 100 = 0
x = -100
Vậy phương trình có nghiệm: x = -100 (0,25đ)
Bài 2 (2đ):
P =
1
2
5
2
1
2
5)24()2(
1
2
332 22
x
x
x
xxx
x
xx (0,5đ)
x nguyên do đó x + 2 có giá trị nguyên
để P có giá trị nguyên thì
1
2
5
x
phải nguyên hay 2x - 1 là ước nguyên của 5 (0,5đ)
=> * 2x - 1 = 1 => x = 1
* 2x - 1 = -1 => x = 0
* 2x - 1 = 5 => x = 3
* 2x - 1 = -5 => x = -2 (0,5đ)
Vậy x =
2;3;0;1 thì P có giá trị nguyên. Khi đó các giá trị nguyên của P là:
x = 1 => P = 8
x = 0 => P = -3
x = 3 => P = 6
x = -2 => P = -1 (0,5đ)
Bài 3 (4đ):
1) a) chứng minh
ABM đồng dạng
CAN (1đ)
b) Từ câu a suy ra:
AN
AM
AC
AB
AMN đồng
dạng
ABC
AMN =
ABC ( hai góc tương ứng) (1,25đ)
2) Kẻ Cy // AB cắt tia Ax tại H (0,25đ)
BAH =
CHA ( so le trong, AB // CH)
mà
CAH =
BAH ( do Ax là tia phân giác)
(0,5đ)
Suy ra:
CHA =
CAH nên
CAH cân tại C
do đó : CH = CA => CH = BK và CH // BK (0,5đ)