
TRƯỜNG THPT TAM ĐẢO ĐÁP ÁN KHẢO SÁT CHUYÊN ĐỀ LẦN 1
NĂM HỌC 2015-2016
Câu 1 (2.0 điểm). Cho hàm số
2 1
x
y
x
(C).
a. Khảo sát và vẽ đồ thị hàm số.
b. Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng
2
3
.
Câu 2 (1.0 điểm). Tìm giá trị lớn nhất và nhỏ nhất của hàm số
3 2
2 3 12 1y x x x
trên [–
1; 5].
Câu 3 (1.0 điểm).
a) Tính:
5 3 8
1 4
log 3 log 6 3log 9
81 27 3A
b) Giải phương trình:
cos3 .cos 1x x
Câu 4 (1.0 điểm).
Trong cụm thi để xét công nhận tốt nghiệp THPT thí sinh phải thi 4
môn trong đó có 3 môn bắt buộc là Toán, Văn, Ngoại ngữ và 1 môn do thí sinh tự
chọn trong số các môn: Vật lí, Hóa học, Sinh học, Lịch sử và Địa lí. Trường X có 40
học sinh đăng kí dự thi, trong đó 10 học sinh chọn môn Vật lí và 20 học sinh chọn
môn Hóa học. Lấy ngẫu nhiên 3 học sinh bất kỳ của trường X. Tính xác suất để trong
3 học sinh đó luôn có học sinh chọn môn Vật lí và học sinh chọn môn Hóa học.
Câu 5 (1.0 điểm). Giải bất phương trình:
4 3
3 2
2 2 1 ( )
2 2
x x x
x x
x x x
Câu 6 (1.0 điểm).
Cho hình chóp S.ABCD có đáy là hình chữ nhật với cạnh AB=2a,
AD=a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB, SC tạo với
đáy một góc bằng 45
0
. Tính thể tích khối chóp S.ABCD và khoảng cách từ điểm A
tới mặt phẳng (SCD).
Câu 7 (1.0 điểm).
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác
ABC
vuông tại B,
AB=2BC, D là trung điểm của AB, E thuộc đoạn AC sao cho AC=3EC, biết phương
trình đường thẳng CD: x-3y+1=0 ,
16
( ;1)
3
E
. Tìm tọa độ các điểm A, B, C.
Câu 8 (1.0 điểm). Giải hệ PT
3 2
2 2
1
,( , ).
3 2 9 3 4 2 1 1 0
xy x x y x y
x y
y x y x x
Câu 9 (1.0 điểm). Cho ba số dương
, ,a b c
thay đổi và thỏa mãn
2a b c
. Tìm GTLN
của biểu thức
2 2 2
ab bc ca
S ab c bc a ca b
-----------------Hết-----------------
Thí sinh không được dùng tài liệu. Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh:………………………………………………SBD:…………………
http://dethithu.net - DE THI THU THPT Quoc Gia - Tai Lieu On Thi.Cap nhat moi ngay.Truy cap TAI NGAY!
Like Fanpage de cap nhat nhieu DE THI THU hon: http://facebook.com/dethithu.net
DeThiThu.Net
TRƯỜNG THPT TAM ĐẢO
ĐÁP ÁN KHẢO SÁT CHUYÊN ĐỀ LẦN 1
NĂM HỌC 2015-2016
Môn: Toán - Khối A, D - Lớp: 12
Câu Nội dung Điểm
1a
Cho hàm số
2 1
x
y
x
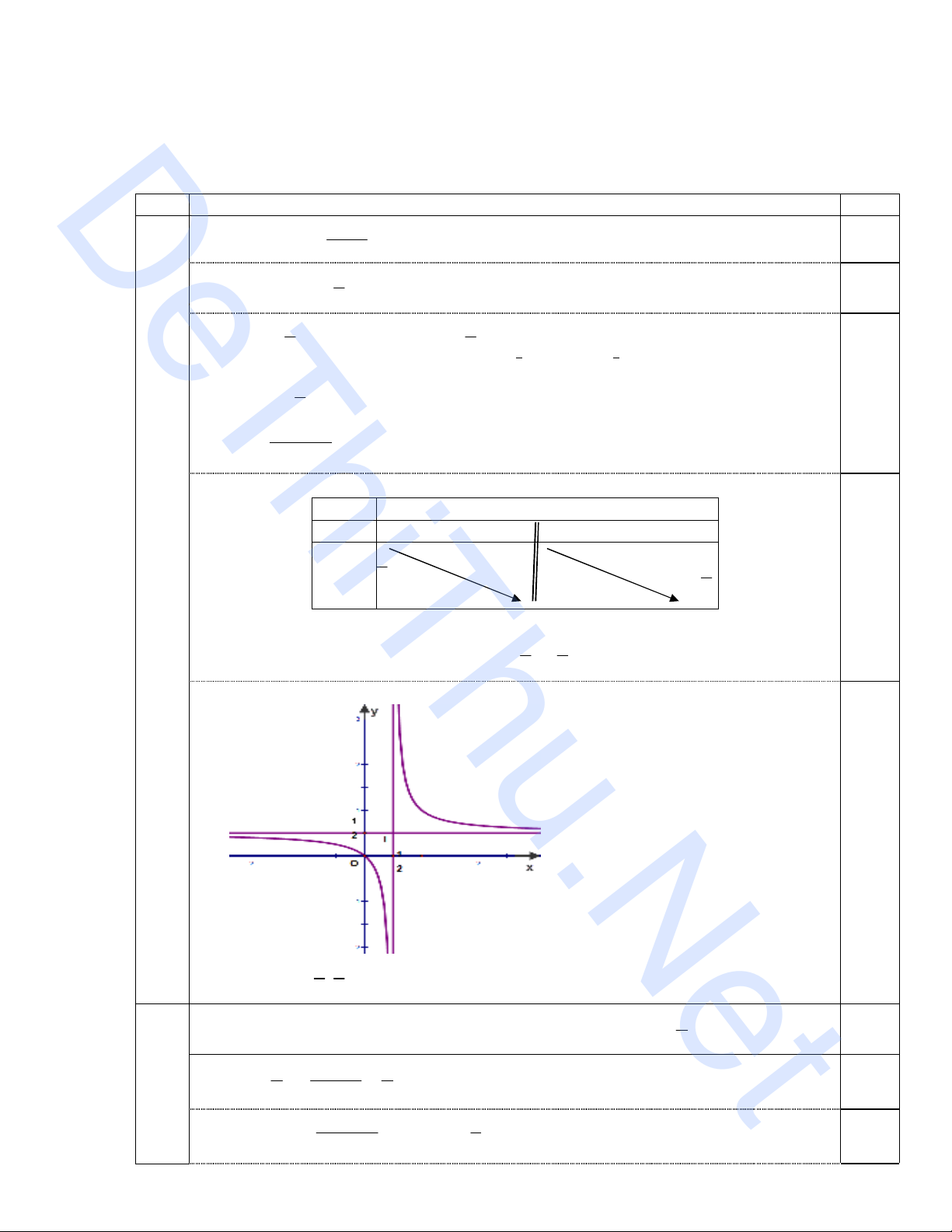
(C). Khảo sát và vẽ đồ thị hàm số 1.0
TXĐ
1
\ .
2
D
0.25
1
lim
2
xy
, đồ thị có TCN
1
2
y
;
1 1
2 2
lim ; lim
x x
y y
, đồ thị hàm số có
TCĐ
1
2
x
.
2
1
' ' 0, .
2 1
y y x D
x
0.25
BBT
x
1/2
y' - -
y
Hàm số nghịch biến trên các khoảng 1 1
; , ;
2 2
.
0.25
Đồ thị
Đồ thị nhận
1 1
;
2 2
I
là tâm đối xứng
0.25
1b
Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng
2
3
. 1.0
Với 0
0 0 0 0
0
2 2
4 2 3 2
3 2 1 3
x
y x x x
x
0.25
Ta có:
2
1 1
'( ) '(2)
9
2 1
f x f
x
0.25
1
2
1
2
http://dethithu.net - DE THI THU THPT Quoc Gia - Tai Lieu On Thi.Cap nhat moi ngay.Truy cap TAI NGAY!
Like Fanpage de cap nhat nhieu DE THI THU hon: http://facebook.com/dethithu.net
DeThiThu.Net

Vậy PT tiếp tuyến tại điểm
2
2;
3
là:
1 8
9 9
y x
0.5
2
Tìm giá trị lớn nhất và nhỏ nhất của hàm số 3 2
2 3 12 1
y x x x
trên [–1; 5]. 1.0
2
' 6 6 12
y x x
0.25
1 1;5
' 0
2 1;5
x
y
x
0.25
Ta có:
( 1) 14, (1) 6, (5) 266
y y y
0.25
Vậy
1;5
1;5
max 266 5, min 6 1
y khi x y khi x
0.25
3
a) Tính:
5 3 8
1 4
log 3 log 6 3log 9
81 27 3
A
0.5
2
3
3 3 2
4
3log 3
4log 5 3log 6
3 3 3A 0.25
3
2log 24 3 4 3 2
5 6 3 5 6 2 845
0.25
b) Giải phương trình:
cos3 .cos 1
x x
0.5
2
cos 4 cos 2 2 2 cos 2 cos 2 3 0
PT x x x x
0.25
cos 2 1
( )
3
cos 2 ( )
2
x
x k k
x L
0.25
4
Tính xác suất để trong 3 học sinh đó luôn có học sinh chọn môn Vật lí và học
sinh chọn môn Hóa học. 1.0
Số phần tử của không gian mẫu là
3
40
n C
0.25
Gọi A là biến cố “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học
sinh chọn môn Hóa học”
Số phần tử của biến cố A là
1 2 2 1 1 1 1
10 20 10 20 20 10 10
. . . .
A
n C C C C C C C
0.5
Vậy xác suất để xảy ra biến cố A là
120
247
A
A
n
Pn
0.25
5
Giải bất phương trình:
4 3
3 2
2 2 1
( )
2 2
x x x
x x
x x x
1.0
ĐK: x > 0, BPT tương đương:
3
3 3
2
2
( 1)( 1) ( 1)
(1)
1 ( 1) 1
( 1) 1
x
x x x
xx x
x x
0.25
Xét hàm số
3
2
( )
1
t
f t
t
trên
0.25
Ta có:
4 2
2
2
3
'( ) 0
1
t t
f t t
t
Mà f(t) liên tục trên
nên f(t) đồng biến trên
.
0.25
(1) có dạng:
3 5
1 1 0
2
f x f x x x x
0.25
6 Tính thể tích khối chóp S.ABCD và khoảng cách từ điểm A tới mặt phẳng
(SCD). 1.0
http://dethithu.net - DE THI THU THPT Quoc Gia - Tai Lieu On Thi.Cap nhat moi ngay.Truy cap TAI NGAY!
Like Fanpage de cap nhat nhieu DE THI THU hon: http://facebook.com/dethithu.net
DeThiThu.Net
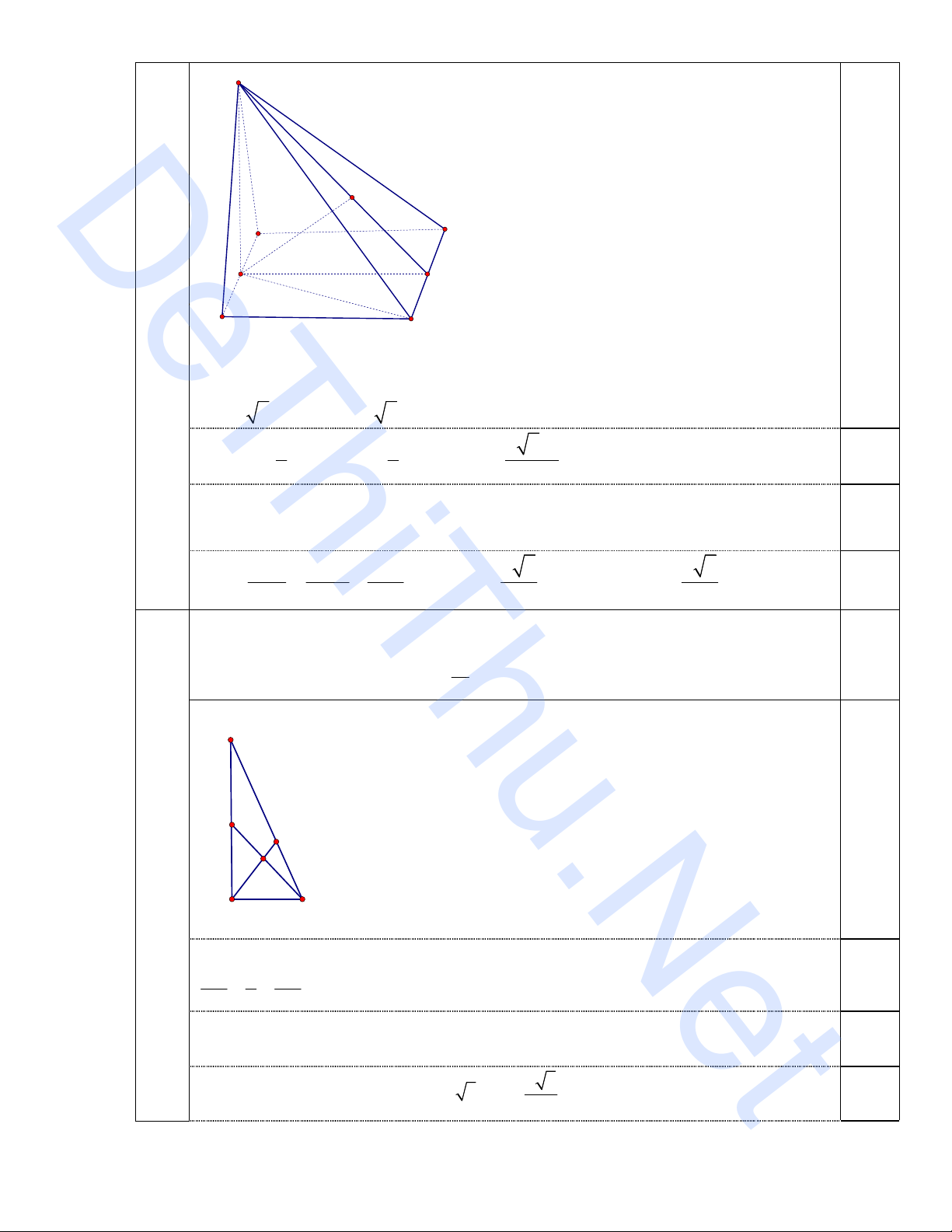
AD
BC
S
HM
P
Ta có HC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD) suy ra
(SC;(ABCD))=(SC;AC)=
SCH
=45 0
HC=a
2
suy ra SH=a
2
0.25
SABCD ABCD
a
V SH S SH AB AD
3
1 1 2 2
. . .
3 3 3
0.25
Gọi M là trung điểm CD, P là hình chiếu của H lên SM khi đó HM
CD; CD
SH
suy ra CD
HP mà HP
SM suy ra HP
(SCD) Lại có AB//CD suy ra AB//
(SCD) suy ra d(A;(SCD))=d(H;(SCD))=HP
0.25
Ta có
HP HM HS
2 2 2
1 1 1
suy ra HP= a
6
3
vậy d(A;(SCD))= a
6
3
0.25
7
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác
ABC
vuông tại B, AB=2BC, D
là trung điểm của AB, E thuộc đoạn AC sao cho AC=3EC, biết phương trình
đường thẳng CD: x-3y+1=0 ,
16
( ;1)
3
E. Tìm tọa độ các điểm A, B, C.
1.0
I
A
B C
DE
Gọi
I BE CD
1
2
BA EA
BC EC
E là chân đường phân giác trong góc ABC 0.25
: 3 17 0
BD BC BE CD BE x y
.
I BE CD
Tọa độ
(5; 2)
I 0.25
Đặt
5
0 2 ; 5;
3
x
BC x AB x AC x EC 0.25
http://dethithu.net - DE THI THU THPT Quoc Gia - Tai Lieu On Thi.Cap nhat moi ngay.Truy cap TAI NGAY!
Like Fanpage de cap nhat nhieu DE THI THU hon: http://facebook.com/dethithu.net
DeThiThu.Net

0 0
2 2 2
45 .cos 45 2
3 (4;5)
3 2
x
CEB IC IB BC
IB IE B
x
IE CE CI IE
(3 1; )
C CD C a a
2
1
2 2 5 4 3 0
3
a
BC BI BC a a a
Với a=1 thì
(2;1), (12;1)
C A
Với a=3 thì
(8;3), (0; 3)
C A
0.25
8
Giải hệ PT
3 2
2 2
1
,( , ).
3 2 9 3 4 2 1 1 0
xy x x y x y
x y
y x y x x
1.0
ĐKXĐ
.
x
Ta có
3 2 3 2 2
1 0
xy x x y x y x x y y xy x y
2
2
1 0
1
y x
x y x y y x
0.25
Với 2
1
y x
thay vào PT thứ 2 ta được
2 2 2 2
3 1 2 9 3 4 6 1 1 0
x x x x x
. Dễ thấy PT vô nghiệm.
Với
y x
thay vào PT thứ 2 ta được
2 2
3 2 9 3 4 2 1 1 0
x x x x x
0.25
2
2
2
2
3 2 9 3 2 1 3 2 1 2
3 2 9 3 2 1 3 2 1 2
x x x x
x x x x
Xét hàm số
2
( ) 2 2
f t t t
ta có
2
2
2
'( ) 2 2 0
2
t
f t t
t
suy ra hàm số
đồng biến.
0.25
Từ đó suy ra
1
3 2 1 .
5
x x x
Vậy HPT có nghiệm
1 1
; ; .
5 5
x y
0.25
9
Cho ba số dương
, ,
a b c
thay đổi và thỏa mãn
2
abc
. Tìm GTLN của biểu
thức
2 2 2
ab bc ca
S
ab c bc a ca b
1.0
Ta có
1
2 2
ab ab ab a b
ab c ab a b c c a c b c a c b c
Đẳng thức xảy ra khi và chỉ khi
a b
a c b c
0.25
Tương tự ta cũng có 1 1
,
2 2 2 2
bc b c ca c a
bc a b a c a ca b c b a b
0.25
Cộng các vế ta được
1 3
.
2 2
a b b c c a
Sa b b c c a
0.25
http://dethithu.net - DE THI THU THPT Quoc Gia - Tai Lieu On Thi.Cap nhat moi ngay.Truy cap TAI NGAY!
Like Fanpage de cap nhat nhieu DE THI THU hon: http://facebook.com/dethithu.net
DeThiThu.Net


























