
TR NG ĐHSPKT H NG YÊN Đ THI K T THÚC H C PH NƯỜ Ư Ề Ế Ọ Ầ
Khoa Khoa h c c b n ọ ơ ả
Đ s : 10ề ố
H c ph n: Toán cao c p 3ọ ầ ấ
Ngày thi:
Th i gian làm bài: 90 phút.ờ
Câu 1(2 đi m):ể Cho hàm s :ố
3 2 2
2 4 3 6z x x y xy x y= − + − − −
1. Tìm các đi m c c tr c a hàm z.ể ự ị ủ
2. T i đi m N (-1, 2), hàm z s tăng hay gi m n u d ch chuy n ra kh i đi m N theoạ ể ẽ ả ế ị ể ỏ ể
h ng l p v i tr c Ox góc 30ướ ậ ớ ụ 0.
3. T i đi m N đó, hãy tìm h ng đ hàm z tăng nhanh nh t.ạ ể ướ ể ấ
Bi u di n trên hình v .ể ễ ẽ
Câu 2(3 đi m):ể Cho h to đ Oxy v i i và j là vector đ n v theo tr c Ox và tr c Oy.ệ ạ ộ ớ ơ ị ụ ụ
Xét tr ng vector ườ
( )
2 2 2
12
2
V x y xy i x y xy j
= + − + − + +
÷
.
1. Ch ng minh r ng tr ng vector V là tr ng có th . Hãy tìm hàm th c a tr ngứ ằ ườ ườ ế ế ủ ườ
vector V tho mãn đi u ki n hàm th đó có giá tr b ng 1 t i g c to đ .ả ề ệ ế ị ằ ạ ố ạ ộ
2. Tính tích phân (tính tr c ti p):ự ế
( )
2 2 2
12
2
x y xy dx x y xy dy
+ − + − + +
÷
L(BA)
v i L là đ ng parabole y=xớ ườ 2 n i 2 đi m A (-1, 1) và B (2, 4).ố ể
3. Ki m ch ng k t qu ph n 2) b ng cách s d ng hàm th tìm đ c ph n 1).ể ứ ế ả ở ầ ằ ử ụ ế ượ ở ầ
Câu 3(2 đi m):ể Cho m t v t th ph ng, trong h to đ Oxy v i tr c Oy h ng th ng đ ngộ ậ ể ẳ ệ ạ ộ ớ ụ ướ ẳ ứ
lên trên, đ c gi i h n b i các đ ng có ph ng trình l n l t là : y = 0, y = b, y = x và y =ượ ớ ạ ở ườ ươ ầ ượ
x-2. M t đ c a v t th đó đ c xác đ nh là p(x, y) = 2 – x - y.ậ ộ ủ ậ ể ượ ị
Hãy xác đ nh đ cao t i đa (thông qua tham s b) c a v t th đ v t th đó không bị ộ ố ố ủ ậ ể ể ậ ể ị
đ d i tác đ ng duy nh t là c a l c tr ng tr ng.ổ ướ ộ ấ ủ ự ọ ườ
Câu 4 (3 đi m):ể Gi i h ph ng trình vi phân:ả ệ ươ
'
'
4 3
10 2
3
y y z x
z y z x
= + −
=− − +
v i đi u ki n: khi x = 0 thì y = 0 và z = 0.ớ ề ệ
Gi ng viên ra đ 1: Khoa / B mônả ề ộ
Gi ng viên ra đ 2:ả ề
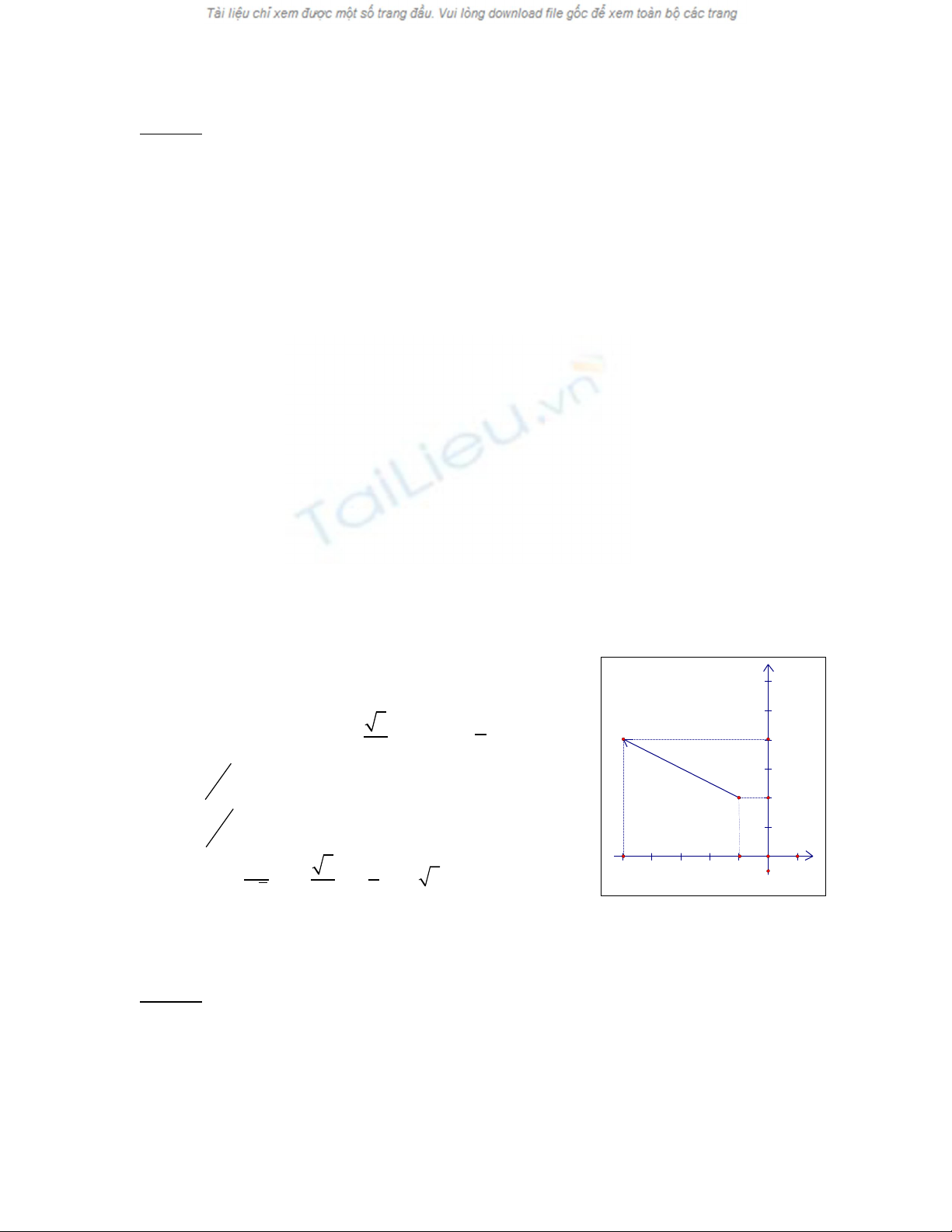
6
4
2
y
-5
x
x
N
Câu 1: 1. Tìm đi m c c tr :ể ự ị
3 2 2
2 4 3 6z x x y xy x y= − + − − −
{
' 2
'
3 4 4 3 0
2 4 6 0
x
y
z x x y
z y x
= − − − =
= − − =
→y=2x+3
Thay vào ta có:
( )
2
2 2
1 1
2 2
1 2
3 4 4 2 3 3 0
3 12 15 0 4 5 0
1 1
5 13
( 1,1), (5,13)
x x x
x x x x
x y
x y
M M
− − + − =
→ − − = → − − =
= − → =
= → =
−
1
( 1,1)M−
( )
2
5,13M
''
6 4
xx
z x r
= − =
-10 26
''
4
xy
z s
=− =
-2 -4
''
2
yy
z t
= =
2 2
s2 - rt 16+20=36 16-52=-36<0
Không c c ti uự ể r=26→ c c ti uự ể
1. Xét N(-1, 2)
Trong đó có cosα=
3
2
cosβ=
1
2
'
'
4
2
x
y
z
N
z
N
= −
=
V y ậ
3 1
4 2. 2 3 1 0
2 2
z
σ
σε
= − + = − + <
V y hàm s gi m n u đi ra kh i đi m N theo h ng l p v i Ox góc 30ậ ẽ ả ế ỏ ể ướ ậ ớ 0.
3. H ng tăng nhanh nh t c a hàm z t i N (-1, 2) là (-4, 2).ướ ấ ủ ạ
Ta có hình v trên:ẽ
Câu 2:
1. Ch ng minh r ng tr ng vector ứ ằ ườ
V
ur
là tr ng có th :ườ ế

( )
2
2 2
, 2 2
2
( , ) 2
y P
P x y x xy y x
y
Q
Q x y x y xy x y
x
∂
= + − → = −
∂
∂
= − + + → = − +
∂
V y ậ
P Q
y x
∂ ∂
=
∂ ∂
→V y tr ng ậ ườ
V
ur
có th .ế
Hàm thế
( , )x y
φ
đ c tìm theo công th c ượ ứ
( , )x y
φ
=
0 0
7
( , 0) ( , )
x
x y
P x y Q x y dy C+ +
∫ ∫
Ta ch n xọ0=0, y0=0 Ta có:
( )
2 2
0 0
2 3 2
2
0 0
( , )
2 3 2
y
x
x y y
y
x y xdx x y xy dy C
x y xy
x y C
φ
=
=
= + − + + +
= + − + + +
÷
∫ ∫
2 3 2
2
( , ) 2 3 2
x y xy
x y x y C
φ
= − + + +
T i O (0, 0), Ф có giá tr là 1 nên C=1. V y hàm Ф ph i tìm là:ạ ị ậ ả
2 3 2
2
( , ) 1
2 3 2
x y xy
x y x y
φ
= − + + +
2. Tính tr c ti p: ự ế
( )
2
2 2
( )
2
2
L BA
y
x xy dx x y xy dy
+ − + − + +
÷
∫
A (-1, 1), B(2, 4), L: y=x2.
( )
( )
12
2 2
2
2
2
1
2 3 5 4
2
12 5 6
3 4 5 4 1
2
2
2 .2
2
2 . 2 2 2
2
5
4 2
2 2 2 3
1 1 1 64
1 2 16 16
2 2 3 3
24
y
x xy x y xy x dx
x
x x x x x x dx
x x x
x x x x dx x
−
−
−−
= + − + − + +
÷
= + − − + +
= − + + = − + +
÷
÷
= − − + − − + +
÷
= −
∫
∫
∫
3. Tính qua hàm th ế
( , )x y
φ

( )
2
2 2
( )
2
2
( ) ( ) ( 1,1) (2,4)
1 1 1 64
1 2 16 16 24
2 3 2 3
L BA
y
x xy dx x y xy dy
A B
φ φ φ φ
+ − + − + +
÷
= − = − −
= − + − − − + + = −
÷ ÷
∫
Câu 3:
1. V hình:ẽ
Ph ng trình c a các bi n:ươ ủ ế
AB: y=0
BC: y=x-2
CD: y=b
DA: y=x
2. Kh i l ng c a v t th :ố ượ ủ ậ ể
( )
( ) ( )
( )
( )
( )
( )
( )
2
0
22
2 2
0 0
2 2
0
2 2
0
0
( , ) 2
1
2 2 2 2 2
2 2
1
4 2 4 4
2
4 6 2 6 2 6
x y
b
D x y
b b
x y
x y
b
b
b
m P x y dxdy dy x y dx
x
dy x xy dy y y y y y y y
dy y y y y
dy y y y b b
= +
=
= +
=
= = + +
= + + = + − + + − + + −
÷
= + + + + −
= + = + = +
∫∫ ∫ ∫
∫ ∫
∫
∫
3. Moment c a v t th đ i v i tr c Oy:ủ ậ ể ố ớ ụ
( ) ( )
( )
( ) ( ) ( )
2
0
23 2
2 2 2
0 0
2 3 2
2 3 2
0
2 2 3 2 3 2
0
, 2
yx
23 2
1 1
2 2 2
3 2
1 1
4 4 6 12 8 4 4
3 2
x y
b
x
D x y
x y
b b
x y
x y
x y
b
b
m xP x y dxdy dy x x y dx
x
dy x x xy dx dy x
dy y y y y y y y
dy y y y y y y y y y y y
= +
=
= + = +
=
=
= = + +
= + + = + +
÷
= + − + + − + + −
= + + − + + + + − + + + −
∫ ∫ ∫
∫ ∫ ∫
∫
∫
2

2 2
0
3 3
2 2 2
0
0
8
4 4 2 4 2 2
3
20 4 20 4 20
4 10 5 5
3 3 3 3 3
b
b
b
dy y y y y y
y b
dy y y y y b b
= + + + + + +
= + + = + + = + +
÷
∫
∫
V y to đ x c a tr ng tâm M là :ậ ạ ộ ủ ọ
3 2
2
2
4 20 4 20
5 5
3 3 3 3
2 6 2 6
x
b b
b b b
Mb b b
+ + + +
= =
+ +
4. Đ v t th không b đ thì Mể ậ ể ị ổ x < 2
Ta có:
2
2
2
4 20
5 4 12
3 3
4 16 0 4 3 16 0
3 3
bb b
bb b b
+ + < +
→ + − < → + − <
Gi i:ả
1,2
3 265
9 256 265 8
b− ±
∆ = + = → =
Chi u cao t i đa là:ề ố
265 3
8
b−
=
Câu 4:
* Ph ng pháp kh :ươ ử
( )
'' ' ' '
'
' '
'
10
4 3 1 4 3 2 2 1
3
4 10 6 6 1
4 10 2 8 2 6 1
2 2 4 1
y y z y y z x
y y z x
y y y y x x
y y x
= + − = + − − + −
÷
= − − + −
= − + − + − + −
= − + −
V y ậ
'' '
2 2 4 1y y y x− + = −
* Gi i ph ng trình thu n nh t:ả ươ ầ ấ
'' '
2 2 0y y y
− + =
Ph ng trình đ c tr ng:ươ ặ ư
2
1
2
2 2 0
4 8 4 2
2 2 1
2
2 2 1
2
i
ii
ii
λ λ
λ
λ
− + =
∆ = − = − → ∆ = ±
+
= = +
−
= = −
V y ph ng trình thu n nh t có hai nghi m:ậ ươ ầ ấ ệ
1
sinx
x
y e=
và
2
cos
x
y e x=


























