SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI DƯƠNG
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 GDTX CẤP TỈNH
NĂM HỌC 2024-2025
Môn thi: TOÁN
Ngày thi: 29/10/2024
Thời gian làm bài: 180 phút, không tính thời gian phát đề
Đề thi có 1 trang
Câu I. (3,0 điểm):
1) Cho hàm số
32
3 93yx x x
có đồ thị
C
.
a) Gọi
,AB
là hai điểm cực trị của
C
. Tính độ dài đoạn
AB
.
b) Cho
0;1M
. Tính khoảng cách từ điểm
M
đến đường thẳng
AB
.
2) Số dân của một thị trấn sau
t
năm kể từ năm
1970
được cho bởi công thức
26 10
5
t
ft t
(
ft
được tính bằng nghìn người). Xem
y ft
là một hàm số xác định
trên
0;
.
a) Dân số của thị trấn đó vào năm
2025
là bao nhiêu?
b) Dân số của thị trấn đó không thể vượt quá bao nhiêu nghìn người?
Câu II. (2,0 điểm):
1) Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh
nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm
vào cơ thể sau
t
giờ được cho bởi công thức
2
2
1
t
Ct t
(đơn vị là miligam/lít). Sau khi tiêm
thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất.
2) Có
6
học sinh nam và
5
học sinh nữ. Chọn ngẫu nhiên
4
học sinh. Tính xác suất để 4
học sinh được chọn có cả nam và nữ.
Câu III. (2,0 điểm):
1) Giải phương trình:
2sin .cos 2sin 1 0x x x cos x
.
2) Giải phương trình:
3 2 56
9 27
xx
.
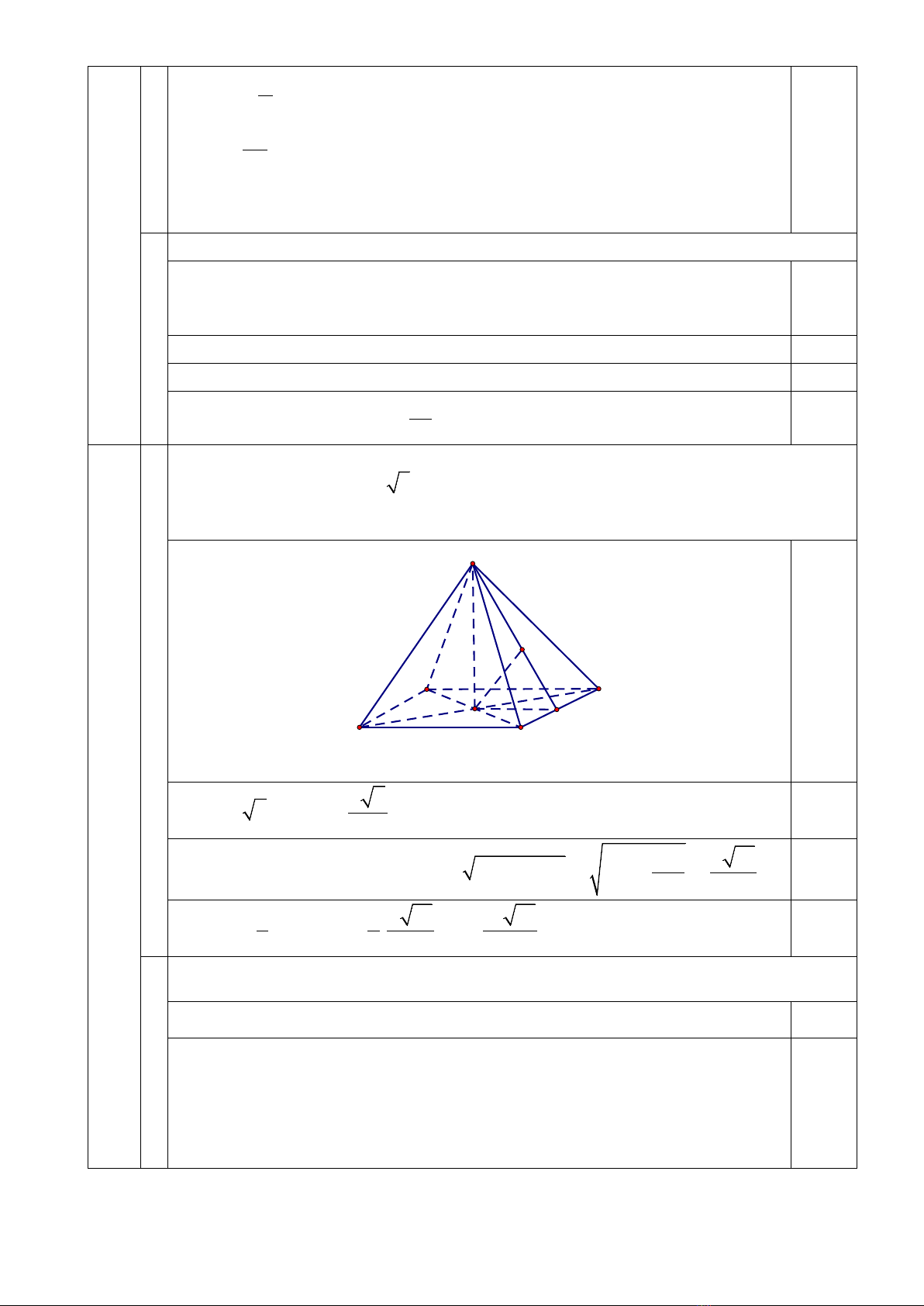
Câu IV. (2,0 điểm):
Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
, tâm
O
. Cho
SO ABCD
và
3SA a
.
1) Tính thể tích khối chóp
.S ABCD
.
2) Tính khoảng cách từ điểm
A
đến mặt phẳng
SCD
.
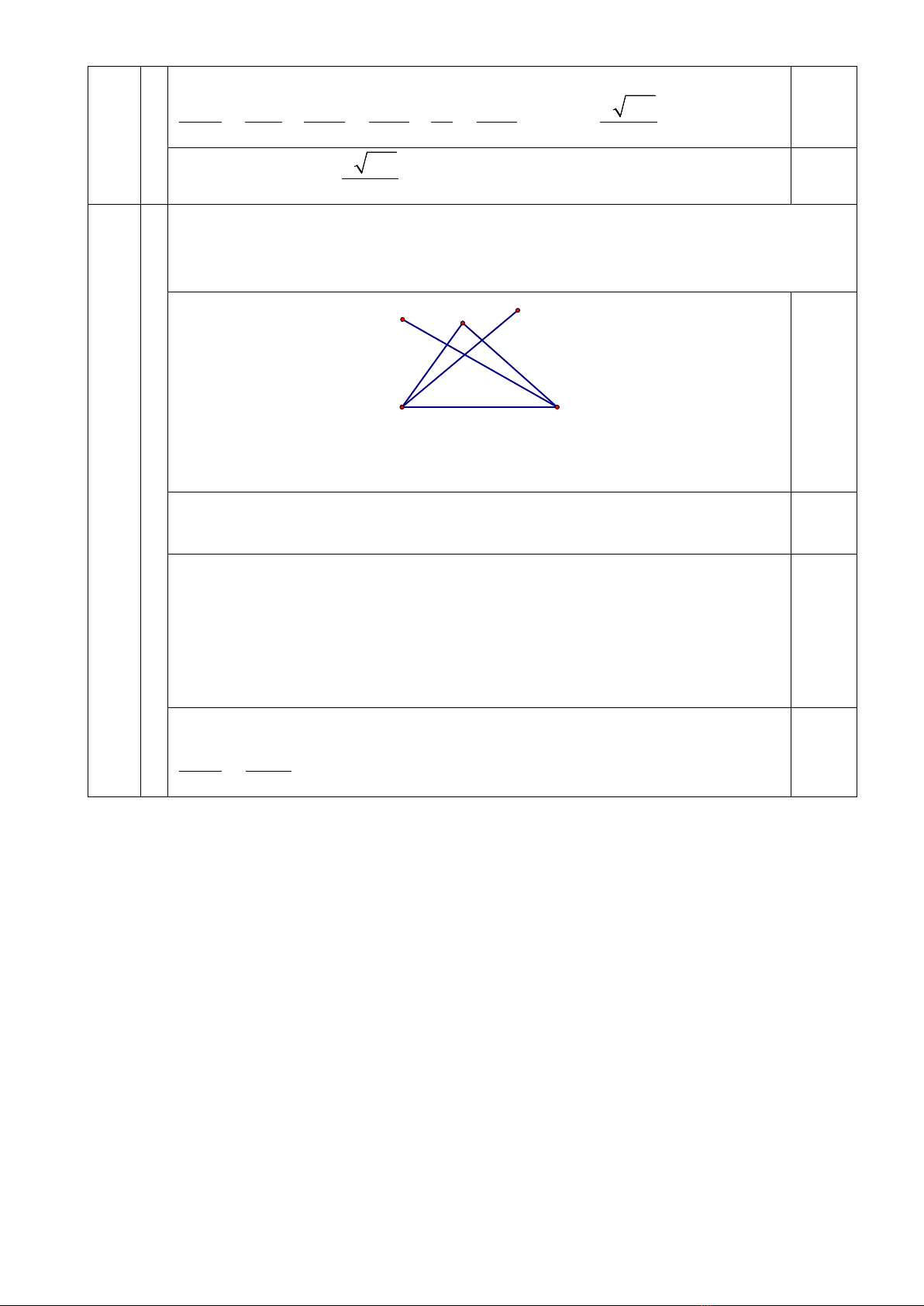
Câu V. (1,0 điểm):
Cho tam giác
ABC
có
2;3A
và hai đường cao kẻ từ
,BC
lần lượt có phương trình là
12
:3230, :340d x y dx y
. Viết phương trình đường thẳng
BC
.
- - - - - - - - - - - - - - HẾT- - - - - - - - - - - - - -
Họ và tên thí sinh: ………………………………………… Số báo danh: ……………………………
Cán bộ coi thi số 1 ……………………………… Cán bộ coi thi số 2 ………………………………
ĐỀ CHÍNH THỨC