UBND HUYỆN PHÚ LƯƠNG
TRƯỜNG THCS PHẤN MỄ I
KỲ THI CHỌN HỌC SINH GIỎI CẤP
TRƯỜNG LỚP 9 NĂM HỌC 2024-2025
Bài thi môn: TOÁN
Thời gian làm bài: 150 phút,
(không kể thời gian phát đề)
Câu 1. (5.0 Điểm).
1. Cho biểu thức: .
a) Khi nào biểu thức có nghĩa? Hãy rút gọn biểu thức .
b) Tính giá trị của biểu thức tại .
c) Tìm giá trị của ẩn để đạt giá trị lớn nhất.
2. Cho và là hai số thỏa mãn: . Hãy tính giá trị của biểu thức .
Câu 2. (5.0 Điểm).
1. Trong mặt phẳng tọa độ , xét hai đường thẳng và . Chứng minh rằng khi thay đổi, giao
điểm của và luôn nằm trên một đường thẳng cố định.
2. Giải phương trình sau: a) . b) .
3. Giải hệ phương trình sau: .
Câu 3. (5.0 Điểm).
Cho đường tròn tâm đường kính BC, dây AD vuông góc với OB tại H. Gọi E, F theo thứ tự
là chân đường vuông góc kẻ từ H đến AB và AC. Vẽ đường tròn tâm G đường kính BH và đường
tròn tâm K đường kính CH.
a) Chứng minh rằng:
b) Chứng minh rằng:
c) Chứng minh rằng: là tiếp tuyến chung của và tâm
Câu 4. (2.0 Điểm).
1. Tính lượng vải cần dùng để tạo ra chiếc nón như hình vẽ. Biết rằng tỉ lệ khấu
hao thực tế khi may một chiếc nón như vậy là (Không kể phần riềm, mép,
phần vải bị thừa).
2. Phần thưởng trong một chương trình khuyến mãi của một cửa hàng bao gồm
2 phần quà bao gồm: Một trong số các đồ gia đình là: chén sứ, tủ lạnh, máy tính;Và một
món trong số các quà lưu niệm như: quả cầu thủy tinh, đồng hồ. Bác Hân tham gia
chương trình đó nên được chọn ngẫu nhiên bóc thăm chọn một phần thưởng.
a) Xác định không gian mẫu của phép thử trong trường hợp trên và có bao nhiêu cách
chọn phần thưởng đó?
b) Cho A là : "Bác Hân chọn được phần thưởng có đồ gia đình là đồ điện".Tính xác suất
biến cố.
Câu 5. (3.0 Điểm).
1. Tìm các cặp số nguyên thỏa mãn phương trình: .
2. Cho ba số thoả mãn Chứng minh chia hết cho
----- HẾT ----
UBND HUYỆN PHÚ LƯƠNG KỲ THI CHỌN HỌC SINH GIỎI CẤP
TRƯỜNG LỚP 9 NĂM HỌC 2024-2025
(Hướng dẫn chấm bao gồm 06 trang)
Bài thi môn: TOÁN
Thời gian làm bài: 150 phút,
không kể thời gian phát đề
HƯỚNG DẪN CHẤM
Đáp án câu 1 Điểm
1. Cho biểu thức: .
a) Khi nào biểu thức có nghĩa? Hãy rút gọn biểu thức .
b) Tính giá trị của biểu thức tại .
c) Tìm giá trị của ẩn để đạt giá trị lớn nhất. 3.25
1.
a. Điều kiện để P có nghĩa là : x
0
; y
0
; xy
1
Ta có :
P=
xy
xyyx
xy
yx
xy
yx
1
2
1:
11
=
xy
xyyxxy
xyxy
xyyxxyyx
1
21
:
11
11
=
xy
xyyx
xy
xyyxyxxyyxyx
1
1
:
1
=
11
1
1
22
yx
xy
xy
xyx
=
x
x
yx
yx
1
2
11
12
0.5
0.5
0.25
0.25
b. Ta thấy x=
32
2
thoả mãn điều kiện x
0
Ta có : x=
32
2
=
3232
322
=4-2
3
=(
3
-1)2
Thay x vào P =
1
2
x
x
, ta có:
P=
325
132
1324
132
2
=
325325
325132
=
2
2
325
3256352
=
1225
1332
=
13
1332
0.5
0.25
c. Với mọi x
0, ta có:
01
2
x
012
2
xx
x+1
x2
1
x
x
1
2
( vì x+1>0)
1
1
2
x
x
P
1
Vậy giá trị lớn nhất của P =1
01
2
x
01
x
1x
x=1
0.25
0.25
0.5
2.Cho và là hai số thỏa mãn: . Hãy tính giá trị của biểu thức . 1.75
Vậy x+y=0
0.25
0.5
0.5
0.5
Đáp án câu 2 Điểm
Câu 2. (5.0 Điểm).
1. Trong mặt phẳng tọa độ , xét hai đường thẳng và . Chứng minh rằng khi thay đổi,
giao điểm của và luôn nằm trên một đường thẳng cố định. 1
Tìm được (d1) cắt (d2) tại M(2m ; 5m-1) với mọi m.
Suy ra quan hệ : ym = 5xm/2 – 1 với mọi m
Do đó khi m thay đổi, giao điểm M của (d1) và (d2) luôn nằm trên đường thẳng cố định
(d) : y = (5/2)x - 1.
1
2.Giải phương trình sau:
a) .
b) . 2.5
Điều kiện: .
Với điều kiện đó, ta có
Nếu thì , không thỏa mãn phương trình.
Nếu thì , ta có
Vậy phương trình đã cho có nghiệm duy nhất .
0.25
0.5
0.25
0.25
Đặt ta có phương trình
vô nghiệm
Vậy tập nghiệm của phương trình là
0.25
0.25
0.5
0.25
3.Giải hệ phương trình sau: . 1.5
Đặt khi đó a, b là nghiệm của phương trình
Do đó:
Vậy
0.5
0.75
0.25
Đáp án câu 3 Điểm
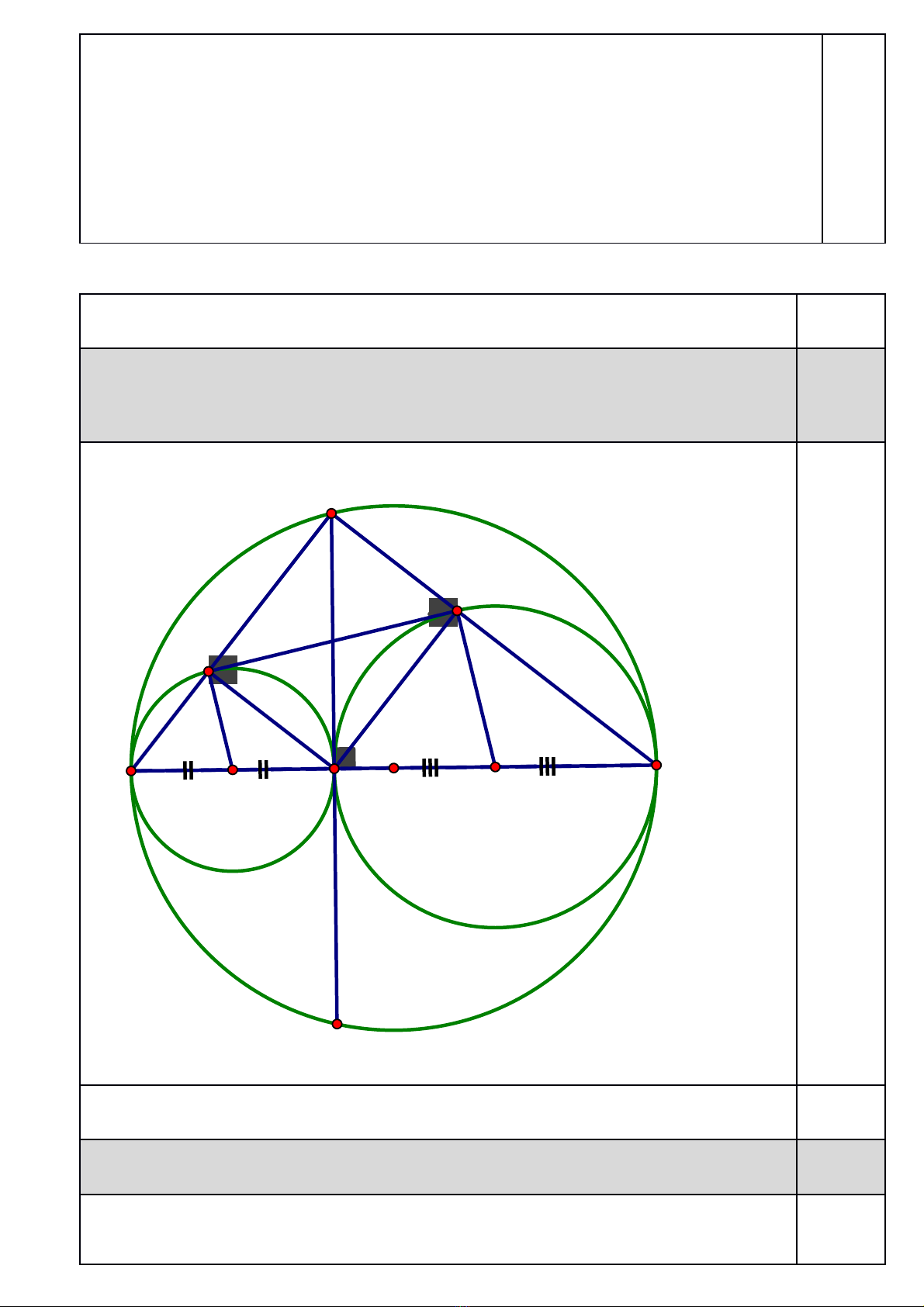
Cho đường tròn tâm O đường kính BC, dây AD vuông góc với OB tại H. Gọi E, F
theo thứ tự là chân đường vuông góc kẻ từ H đến AB và AC. Vẽ đường tròn tâm G
đường kính BH và đường tròn tâm K đường kính CH.
a) Chứng minh rằng:
1.0
Hình vẽ:
F
E
H
D
O
B
C
A
a)Chứng minh 1.25
b) Chứng minh rằng: 2.5
b)
Chứng minh tứ giác AEHF là hình chữ nhật.
Sử dụng định lý Pytago vào ta có:
1
0.5