SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP THÀNH PHỐ
NĂM HỌC 2024-2025
MÔN: TOÁN
Ngày thi: 14/03/2025
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Câu 1: (4 điểm)
1. Cho 2 số a, b thỏa a – b = 3. Tính giá trị của biểu thức 3 3
9
M a b ab
2. Giải phương trình:
2025 16 3 41
x x
Câu 2: (6 điểm)
1. Thầy Bình chấm bài kiểm tra Toán lớp 9A có 45 bạn, sót bạn An nên điểm trung bình là
7,55. Sau đó chấm bổ sung được 7,56. Tính điểm bạn An.
2. Ông Năm có cuộn dây 100m làm rào chắn cho hồ cá dạng hình chữ nhật, biết rằng ông
Năm không rào cả mặt tiếp xúc bờ. Tìm cách rào sao cho diện tích hồ cá đạt giá trị lớn
nhất.
3. Ba bạn Phúc, Lộc, Thọ lần lượt viết lên bảng các số tự nhiên từ 1 đến 9 sao cho số người
trước không trùng số người sau. Tính xác suất số bạn Phúc chia hết cho số bạn Lộc, số
bạn Lộc chia hết cho số bạn Thọ.
Câu 3: (5 điểm)
1. Cho tam giác ABC nhọn, lấy điểm P thuộc miền trong của tam giác ABC sao cho
. Từ P kẻ PM BC tại M, PK AC tại K. Gọi D là trung điểm AB. Chứng
minh: DM = DK.
2. Cho tam giác ABC nội tiếp (O; R). Lấy điểm M thuộc cung BC, từ M kẻ MP, MQ, MR
lần lượt vuông góc với AB, BC, CA tại P, Q, R.
a) Chứng minh: P, Q, R thẳng hàng.
b) Kẻ CS AM tại S, CE AB tại E. Chứng minh: PQ = ES
Câu 4: (3 điểm)
1. Cho số tự nhiên n cộng thêm với 26, tiếp đó thêm 3 chữ số vào bên phải của số đã cho.
Biết rằng sau khi thêm, số đó là tổng của các số tự nhiên liên tiếp từ 1 đến n. Tìm n và 3
chữ số đã thêm.
2. Cho tập hợp
1;2;3...;100
X. Hỏi sẽ lấy ra ít nhất bao nhiêu số sao cho chắc chắn:
a. “Trong các số đã lấy có 5 số tự nhiên liên tiếp”
b. “Trong các số đã lấy có 2 số có tổng chia hết cho 5”
Câu 5: (2 điểm)
Cho đa thức
2,P x x ax b a b
. Biết rằng đa thức P(x) sẽ gọi là đa thức“tốt” nếu P(x)
thỏa mãn có ít nhất một nghiệm nguyên và trị tuyệt đối của a và b không vượt quá 2025.
a) Chứng minh rằng nếu P(x) là đa thức “tốt” thì P(-x) cũng là đa thức “tốt”.
b) Gọi S(x) là tổng của các đa thức “tốt”. Chứng minh S(x) không có nghiệm thực.
-HẾT-
ĐỀ CHÍNH THỨC
(Đề thi gồm 01 trang)
HƯỚNG DẪN GIẢI
Câu 1: (4 điểm)
1. Cho 2 số a, b thỏa a – b = 3. Tính giá trị của biểu thức 3 3 9M a b ab
3
3 3 3
9 3 9 3 3 .3 9 27M a b ab a b ab a b ab ab ab .
2. Giải phương trình: 2025 16 3 41x x
2025 16 3 41x x ĐK: 16
2025 3
x
2
2025 16 3 2 2025 16 3 41x x x x
2 2025 16 3 360 2x x x ĐK: 180x
2 2
4 2025 16 3 4 1440 360x x x x
2
16 22796 0x x
0x hoặc 5699
4
x
Thử lại: nhận 0x, loại 5699
4
x
Vậy: x=0 là nghiệm của phương trình.
Câu 2: (6 điểm)
1. Thầy Bình chấm bài kiểm tra Toán lớp 9A có 45 bạn, sót bạn An nên điểm trung
bình là 7,55. Sau đó chấm bổ sung được 7,56. Tính điểm bạn An.
Tổng số điểm của 44 bạn (không có An) là: 7,55.44 = 332,2 điểm
Điểm An là: 7,56.45 – 332,2 = 8 điểm.
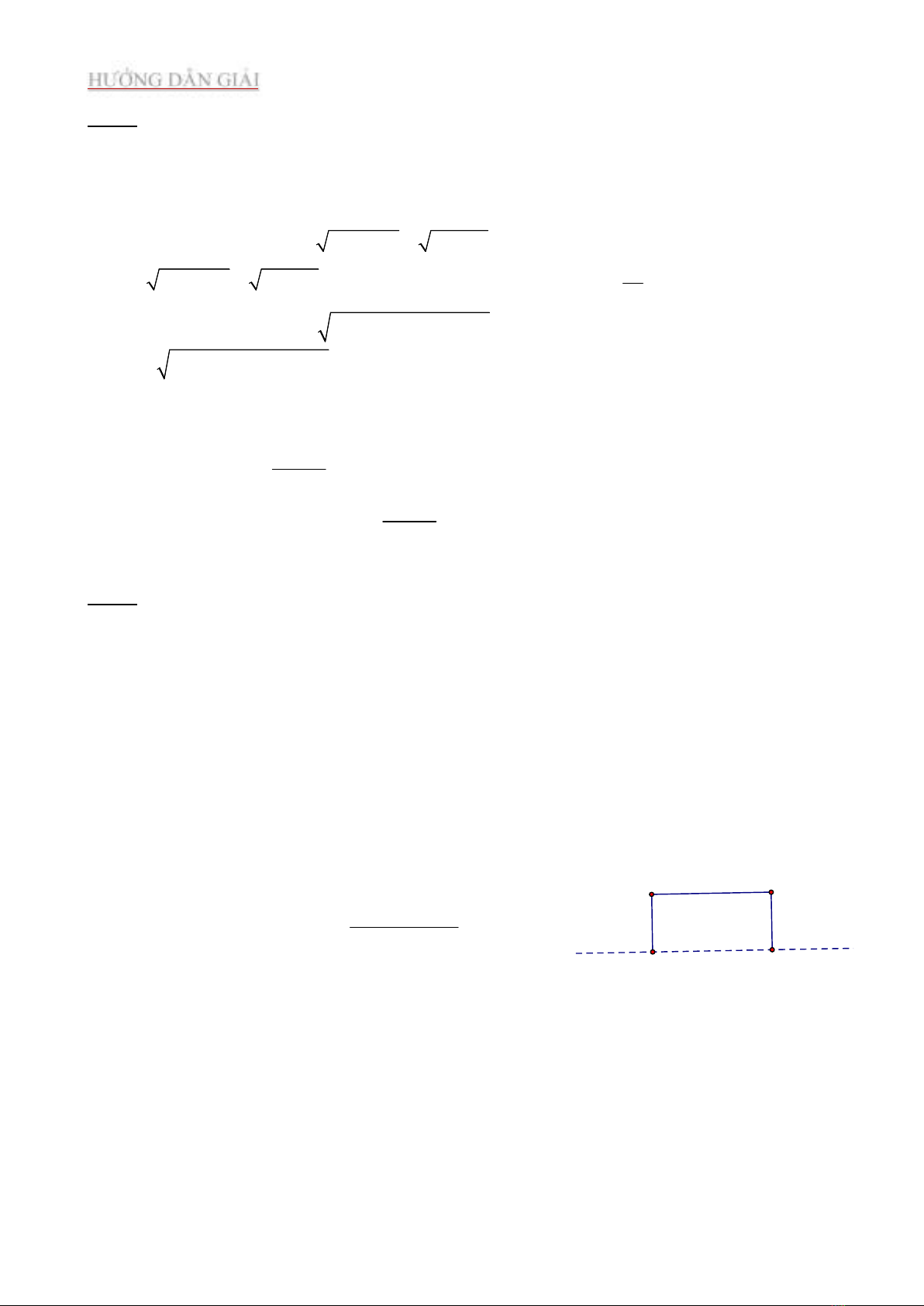
2. Ông Năm có cuộn dây 100m làm rào chắn cho hồ cá dạng hình chữ nhật, biết rằng
ông Năm không rào cả mặt tiếp xúc bờ. Tìm cách rào sao cho diện tích hồ cá đạt giá
trị lớn nhất.
Giả sử, cái ao cá hình chữ nhật ông Năm muốn rào có dạng như hình vẽ
Diện tích cái ao
100 2S x x
2
2 100 2
2 2 100 2 2500
2
x x
S x x
1250S
Dấu “=” xảy ra khi 2 100 2 25x x x
Vậy: ông Năm cần rào một cái ao có chiều rộng là 25m, chiều dài song song với bờ
50m thì diện tích cái ao đạt GTLN là 1250 m2.
3. Ba bạn Phúc, Lộc, Thọ lần lượt viết lên bảng các số tự nhiên từ 1 đến 9 sao cho số
người trước không trùng số người sau. Tính xác suất số của bạn Phúc chia hết cho
số của bạn Lộc, số của bạn Lộc chia hết cho số của bạn Thọ.
Bạn thứ nhất có 9 cách chọn để viết số
Bạn thứ hai có 8 cách chọn để viết số
100 - 2x
x
xbờ
Bạn thứ ba có 7 cách chọn để viết số
Số các trường hợp xảy ra là: 9.8.7 = 504 cách chọn.
Do Phúc viết đầu tiên, nếu số của Phúc viết là các số
1;2;3
thì không có số nào mà Lộc có
thể viết để thỏa mãn yêu cầu bài toán. Do đó, Phúc có 6 cách để viết số lên bảng
4;5;6;7;8;9
Phúc viết số 4 Lộc có 2 cách viết
1;2
Giả sử Lộc viết số 1 thì Thọ không có cách viết số nào thỏa đề bài
Lộc viết số 2, Thọ viết số 1
ta có 1 bộ số thỏa yêu cầu bài toán là (4;2;1)
Phúc viết số 5 Lộc có 1 cách viết là số 1 Thọ không có cách viết
trường hợp Phúc viết số 5 thì không có bộ số thỏa.
Phúc viết số 6 Lộc có 3 cách viết là
1;2;3
Tương tự như trên, Lộc không thể viết số 1 Lộc viết số 2 hoặc 3.
Với mỗi trường hợp, ta tìm được 2 bộ số là (6; 2; 1) và (6; 3; 1)
Phúc viết số 7. Tương tự, không tìm được bộ số.
Phúc viết số 8. Tương tự, tìm được 3 bộ số
Phúc viết số 9. Tương tự, tìm được 1 bộ số.
Vậy có tổng cộng 1 + 2 + 3 + 1 = 7 khả năng được chọn.
Vì vậy: xác suất để xảy ra các trường hợp thỏa yêu cầu bài toán là
7 1
504 72
.
Tham khảo thêm bảng :
Ph
úc
L
ộ
c
Th
ọ
4
2
1
6
2
1
8
2
1
6
3
1
9
3
1
8
4
1
8
4
2
Câu 3: (5 điểm)
1. Cho tam giác ABC nhọn, lấy điểm P thuộc miền trong của tam giác ABC sao cho
. Từ P kẻ PM BC tại M, PK AC tại K. Gọi D là trung điểm AB. Chứng
minh: DM = DK.
Gọi N đối xứng M qua D
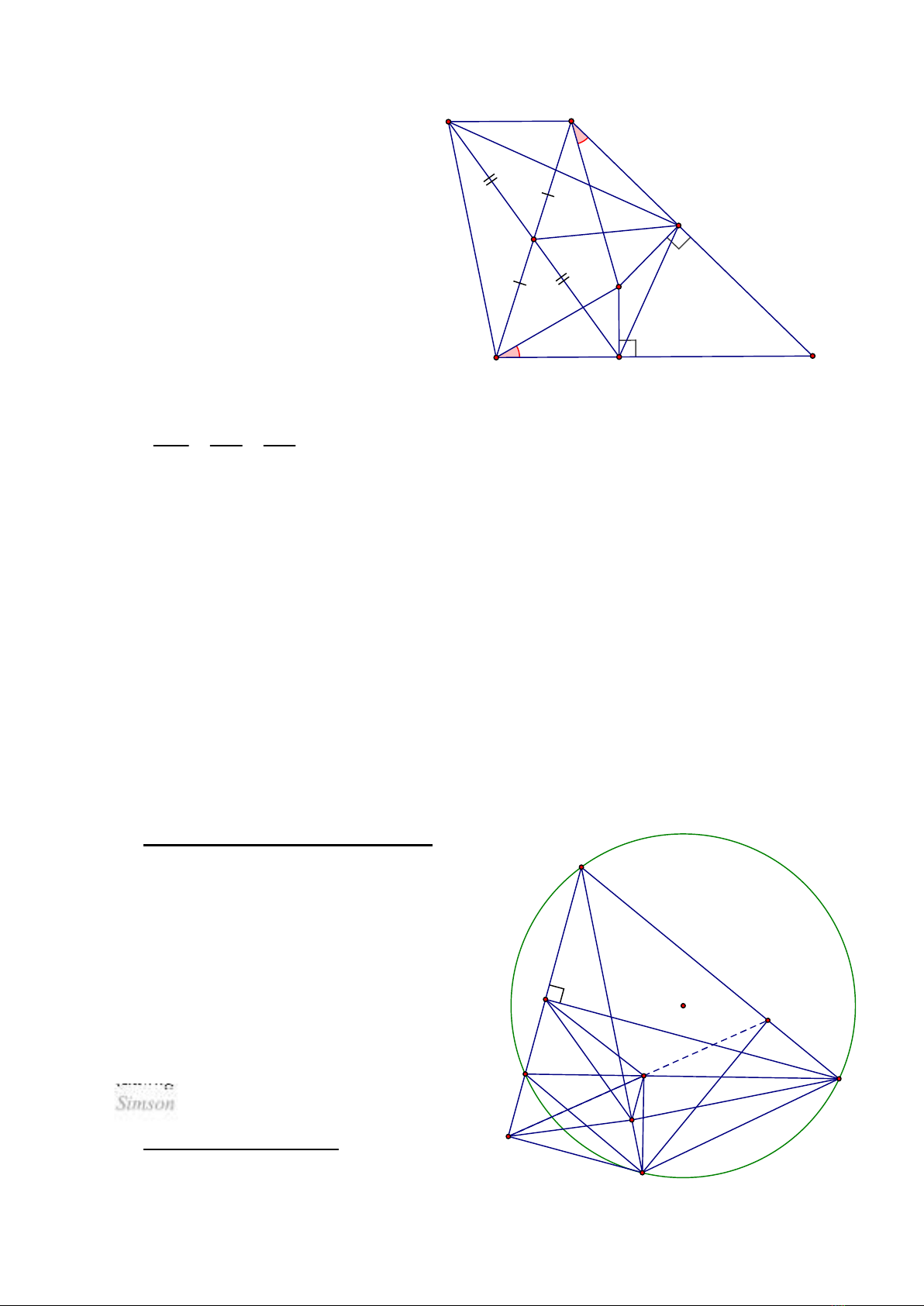
Suy ra AMBN là hình bình hành
Suy ra: AN = BM và AN // BM
Do AN // BC (AN // BM) nên chứng
minh được
0
180KAN ACB (1)
Mặt khác: tứ giác MPKC nội tiếp
Nên
0
180KPM ACB (2)
Từ (1) và (2) suy ra:
KAN KPM
Chứng minh được: PKA đồng dạng
PMB (gg)
Suy ra:
PK AK AK MB AN
PM MB AN
Và:
KAN KPM (cmt)
Nên: PKM đồng dạng AKN (cgc)
Suy ra:
PKM AKN
Suy ra:
0
90MKN
DK = DM
2. Cho tam giác ABC nội tiếp (O; R). Lấy điểm M thuộc cung BC, từ M kẻ MP, MQ,
MR lần lượt vuông góc với AB, BC, CA tại P, Q, R.
a) Chứng minh: P, Q, R thẳng hàng.
b) Kẻ CS AM tại S, CE AB tại E. Chứng minh: PQ = ES.
a) Chứng minh: P, Q, R thẳng hàng.
BQMP nội tiếp
PQM PBM (1)
MQRC nội tiếp
0
180MQR MCR (2)
MCR MBP ABMC nt (3)
Từ (1), (2), (3)
0
180MQR MQP
Suy ra: P, Q, R thẳng hàng.
(đường thẳng PQR là đường thẳng
Simson)
b) Chứng minh: PQ = ES
Ta có: 5 điểm M, S, Q, R, C cùng thuộc
đường tròn đường kính MC.
N
D
K
M
P
C
B
A
E
S
P
R
Q
O
C
B
A
M
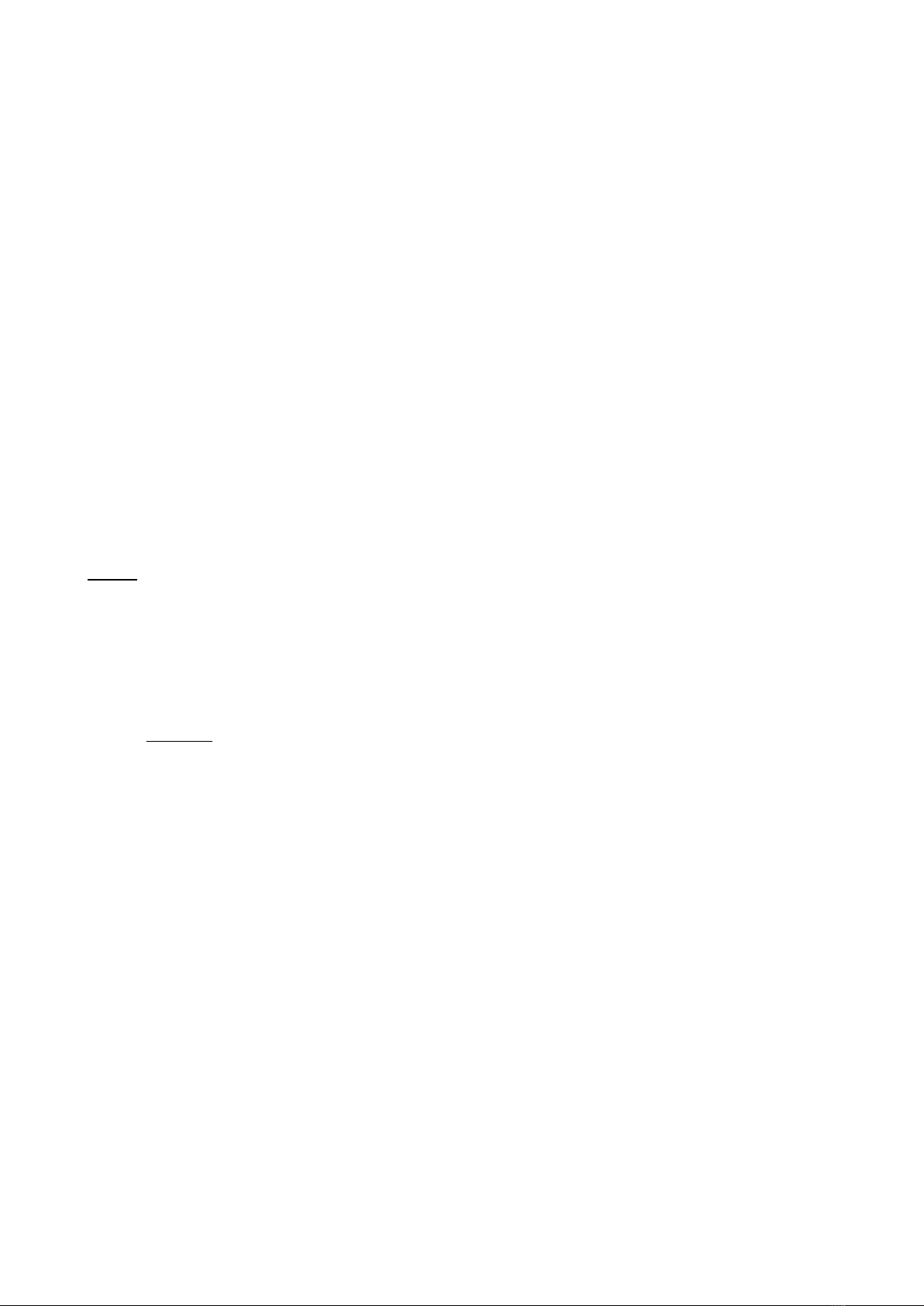
Do đó:
PQS RCS
(4)
C/m được: AESC nội tiếp nên ta có
PES RCS
(5)
Từ (4) và (5)
SQP SEP
tứ giác PEQS nội tiếp
Mặt khác:
0
90
MBC BMQ
0
90
SAC SCA
MBQ SAC
Do đó:
BMQ SCA
Mà:
BMQ BPQ
(BQMP nội tiếp)
Nên:
BPQ SCA
hay
BPQ RCS
(6)
Từ (4) và (6) suy ra:
PQS BPQ
QS // EP QSPE là hình thang. (*)
QS // PE
0
180
QSP EPS
Mà:
0
180
QSP PEQ (PEQS nội tiếp)
Nên:
EPS PEQ
(**)
Từ (*) và (**) QSPE là hình thang cân PQ = ES.
Câu 4: (3 điểm)
1. Cho số tự nhiên n cộng thêm với 26, tiếp đó thêm 3 chữ số vào bên phải của số đã cho.
Biết rằng sau khi thêm, số đó là tổng của các số tự nhiên liên tiếp từ 1 đến n. Tìm n và 3
chữ số đã thêm.
Từ giả thiết, suy ra:
1
26 .1000 0 999
2
n n n k k
2
1999 52000 2
n n k
2
0 1999 52000 1998
n n
2025 2025
n
2025
n
325
k
Vậy:
2025
n
và ba số đã thêm vào bên phải lần lượt là 3, 2, 5.
2. Cho tập hợp
1;2;3...;100
X. Hỏi sẽ lấy ra ít nhất bao nhiêu số sao cho chắc
chắn:
a. “Trong các số đã lấy có 5 số tự nhiên liên tiếp”.
Ta chia tập
1;2;3...;100
X thành 10 tập hợp con
1 2 3 10
; ; ;...;
X X X X
sao cho tập
1
X
chứa các
phần tử từ 1 đến 10, tập
2
X
chứa các phần tử từ 11 đến 20, tập
3
X
chứa các phần tử từ 21 đến 30,
…., tập
10
X
chứa các phần tử từ 91 đến 100
Ta lấy ra từ mỗi tập con 8 phần tử có các chữ số tận cùng là 1,2,3,4,6,7,8,9.
Khi đó ta lấy ra được tất cả 80 số mà không có 5 số tự nhiên nào liên tiếp.
Ta chứng minh cần phải lấy ít nhất 81 số để thỏa mãn đề bài.