UBND HUYỆN YÊN ĐỊNH
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
LỚP 7 CẤP HUYỆN
NĂM HỌC 2023 – 2024
Môn: Toán
Thời gian: 120 phút (không kể thời gian giao đề)
Ngày thi 26 tháng 3 năm 2024
Câu 1: (4 điểm)
1. Tính bằng cách hợp lí:
a) A =
2000 4 24 5 20
2024 24 2024 7 24

b) B =
1 1 1 1
1 1 1 .... 1
3 4 5 2024
2. Tìm x, y biết:
2024 2
2 6 3 12 0x x y
Câu 2: (4 điểm)
1. Tìm các số x, y, z biết và
2 2 2
9 3 60x y z
2. Cho đa thức bậc hai:
2
f x ax bx c
(x là ẩn; a, b, c là hệ số).
Biết rằng:
0 2020f
,
,
1 2023f
. Tính
2f
.
Câu 3: (4 điểm)
1. Cho các số a,b,c,d thỏa mãn:
dabc
chia hết cho 3.
Chứng minh rằng:
3 3 3 3
adbc
cũng chia hết cho 3
2. Cho a, b là hai số tự nhiên khác 0. Chứng minh rằng: Nếu a; a+b; a+2b là các số
nguyên tố lớn hơn 3 thì b chia hết cho 6.
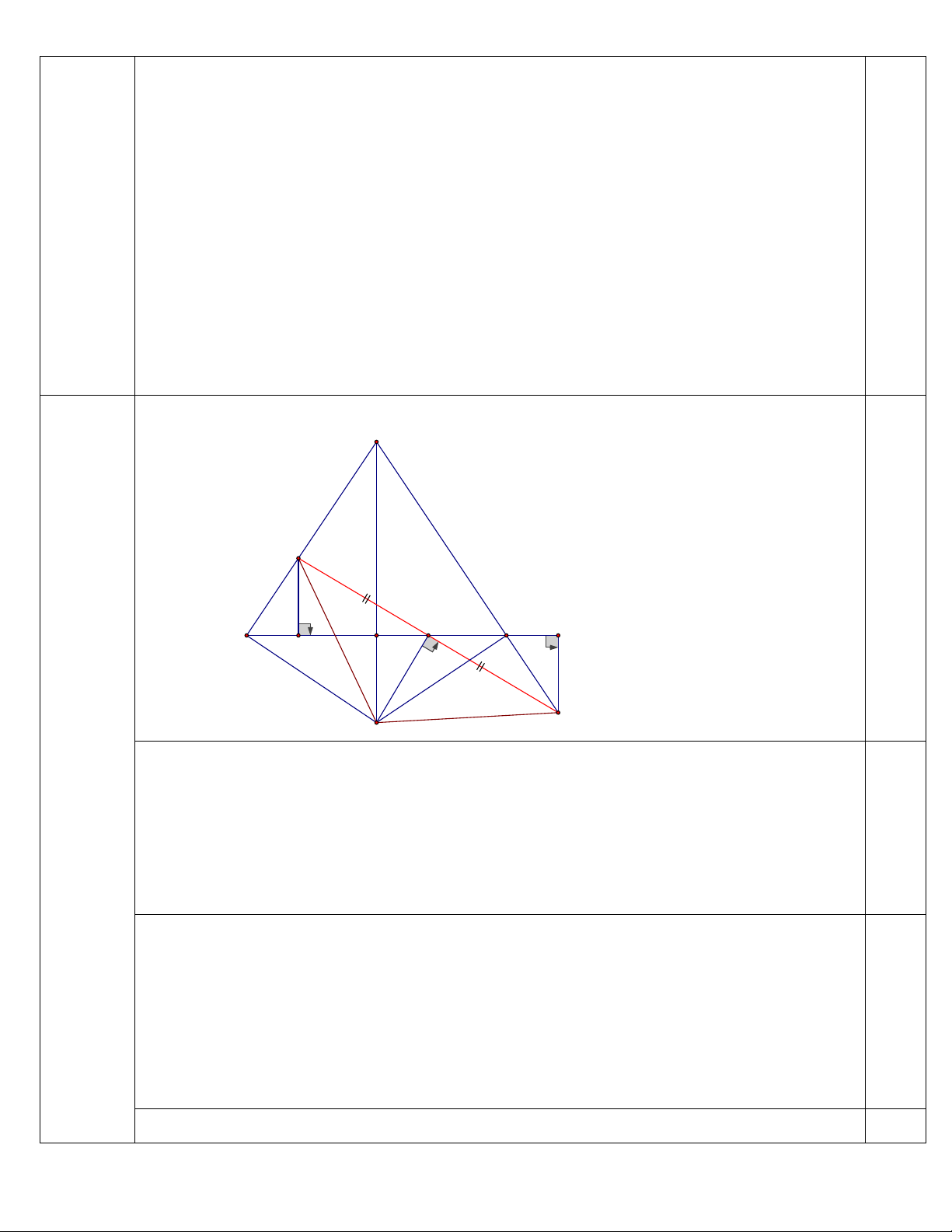
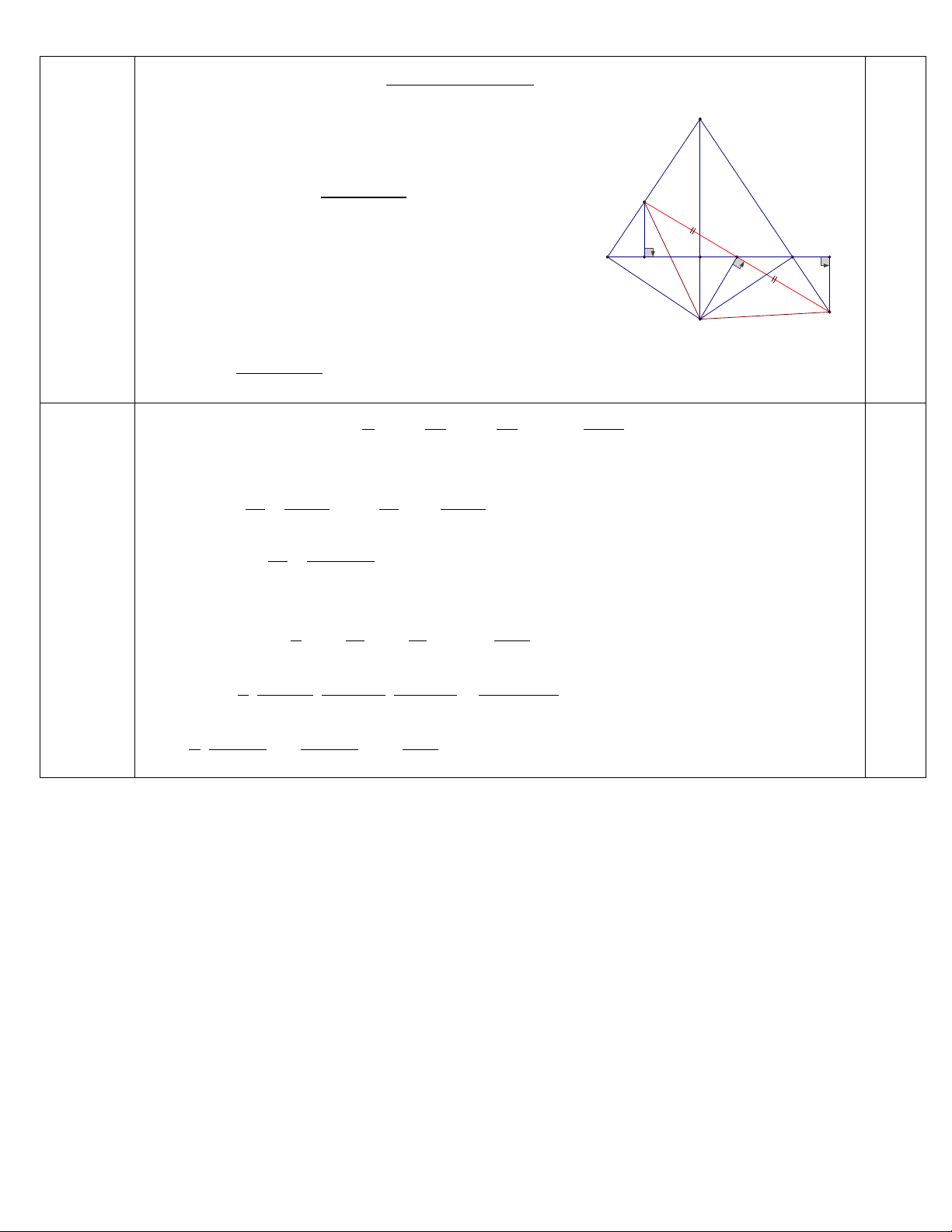
Câu 5: (6 điểm) Cho ABC c n t i , trên c nh BC l y điểm D (D không trùng với B và
C), trên tia đối c a tia CB l y điểm E sao cho BD CE, qua D k đ ờng th ng vuông g c
với BC cắt B t i M, qua E k đ ờng th ng vuông g c với BC cắt C t i N.
1. Chứng minh rằng: DM EN.
2. Chứng minh rằng đ ờng th ng BC cắt MN t i trung điểm c a MN.
3. Đ ờng th ng vuông g c với MN t i cắt tia ph n giác c a
BAC
t i O.
Chứng minh rằng:
2 2 2
. . .
2
OM ON MN OM ON ON MN MN OM

Câu 6: (2 điểm) Chứng tỏ rằng:
2 3 2024
1 1 1 1
1 1 1 ... 1 3
2 2 2 2
P
---------------Hết-----------------
Lưu ý: Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………………….SBD:…………………………….
54
3zy
x
ĐỀ THI CHÍNH THỨC
H- íng dÉn chÊm m«n to¸n khèi 7
Câu
Đáp án
Biểu
điểm
1
(4 điểm)
1.
a) A =
2000 4 24 5 20
2024 24 2024 7 24

5 5 5
( 1 1) 0
7 7 7
b) B =
1 1 1 1
1 1 1 .... 1
3 4 5 2024
=
4 5 6 2025
. . ...
3 4 5 2024
=
2025 675
3
1
0.75
0.25
2. Tìm x; y biết:
2024 2
2 6 3 12 0x x y
Vì:
2024
2
2 6 0
3 12 0
x
xy

mọi x,y
Nên để:
2024 2
2 6 3 12 0x x y
thì:
2024
2
2
3
2 6 0 3
9 3 12 0
3 12 0
3 12 0
x
xx
y
xy
xy

 




33
9 3 12 0 1
xx
yy




Vậy:
( , ) (3; 1),( 3; 1)xy
0,25
0,25
0,5
0.5
0.5
0.5
0.5
2
(4 điểm)
1. Tìm các số x, y, z biết và
2 2 2
9 3 60x y z
Đặt
3
3x 4
45 5
k
x
yz
k y k
zk
Mà:
2 2 2
9 3 60x y z
nên:
2 2 2
9( ) (4 ) 3(5 ) 60
3
kkk
Suy ra:
2
60 60 1kk
0.5
0.75
0.75
54
3zy
x
Với k 1 thì
1
3
4
5
x
y
z

Với k -1 thì:
1
3
4
5
x
y
z

Vậy :
11
; ; ( ; 4;5),( ; 4; 5)
33
x y z



2. Cho đa thức bậc hai:
2
f x ax bx c
(x là ẩn; a, b, c là hệ số).
Biết rằng:
0 2020f
,
,
1 2023f
. Tính
2f
.
Xét x = 0:
(0) 2020 2020fc
Xét x = 1:
(1) 2021 2021 1f a b c a b
(1)
Xét x = -1:
( 1) 2023 2023 3f a b c a b
(2)
Cộng vế (1) và (2) suy ra a 2
Thay a 2 vào (1) tìm đ ợc: b -1
Từ đ tìm đ ợc
2
2x 2020f x x
Suy ra: ( )
0.5
0.5
0.5
0.5
3
(4 điểm)
1. Cho các số a,b,c,d thỏa mãn:
dabc
chia hết cho 3.
Chứng minh rằng:
3 3 3 3
adbc
cũng chia hết cho 3
Vì
dabc
chia hết cho 3 nên
3a b c d
Nên ta đi chứng minh:
3 3 3 3
a d 3bc
Xét
32
a ( 1) ( 1)( 1) 3a a a a a a
T ơng tự:
3
3
3
3
3
3
bb
cc
dd
Nên
3 3 3 3
(a d ) ( ) 3b c a b c d
Mà
3a b c d
nên
3 3 3 3
a d 3bc
Ta đ ợc điều phải chứng minh.
0.5
0.5
0.5
0.5
2. Cho a, b là hai số tự nhiên khác 0. Chứng minh rằng: Nếu a; a+b; a+2b là
các số nguyên tố lớn hơn 3 thì b chia hết cho 6.
. Vì a; a+b; a+2b là các số nguyên tố lớn hơn 3 nên là các số l và không chia
hết cho 3:
a + b - a = b là số chẵn nên chia hết cho 2 (1)
0,25
0,5
Mặt khác a; a+b; a+2b không chia hết cho 3 nên khi chia 3 số đ cho 3 sẽ d 1
hoặc 2
Suy ra khi chia 3 số đ cho 3 sẽ c 2 sô cùng d :
+ Nếu a và a+b cùng d khi chia cho 3 thì a+b - a b chia hết cho 3
+ Nếu a và a+2b cùng d khi chia cho 3 thì a+2b - a 2b chia hết cho 3 suy ra b
chia hết cho 3 ( Vì (2,3) 1)
+ Nếu a+b và a+2b cùng d khi chia cho 3 thì (a+2b) - (a+b) b chia hết cho 3
Cả 3 tr ờng hợp ta đều c b chia hết cho 3 (2)
Từ (1) và (2 ) ta c b chia hết cho 6 ( Vì (2,3) =1)
0.25
0.25
0,5
0,25
4
(6 điểm)
1. Ta có
Nên
Xét hai tam giác MBD và tam giác NCE ta có :
BD=CE;
;
Suy ra: (cặp c nh t ơng ứng)
0.5
0.75
0.75
2.
vuông t i D: (tổng hai góc nhọn trong tam giác vuông)
vuông t i E: (tổng hai góc nhọn trong tam giác vuông)
Mà (đối đỉnh) nên
(cặp c nh t ơng ứng)
Vậy cắt t i điểm là trung điểm c a
0.75
0.75
0.5
3. Đ ng th ng vu ng g c với MN t i I c t tia ph n giác c a
BAC
t i O
..MDB NEC g c g
DM EN
MDI
0
90DMI MID
NEI
0
90ENI NIE
MID NIE
DMI ENI
( . . )MDI NEI g c g IM IN
BC
MN
I
MN
1
2
1
O
I
M
N
H
B
C
A
D
E
Chứng minh rằng :
2 2 2
. . .
2
OM ON MN OM ON ON MN MN OM

Ta có :3 c nh OM, ON, MN t o thành
OMN
Đặt OM a, ON b, MN c
Bài toán trở thành :
2 2 2
2
abc ab bc ca

Theo BĐT tam giác ta c :
2
2
2
a b c a ab ac
b a c b ab bc
c a b c ac bc
Từ đ ta c
2 2 2 2( )a b c ab bc ca
Suy ra
2 2 2
2
abc ab bc ca

0.25
0.25
0.75
0.5
0.25
Câu 6
(2 điểm)
Chứng tỏ rằng:
2 3 2024
1 1 1 1
1 1 1 ... 1 3
2 2 2 2
P
Ta có
2 2 2( )
nn nN
1 1 1 1
11
2 2 2 2 2 2
1 2 1
12 2(2 2)
n n n n
n
nn

Áp dụng vào P ta đ ợc :
P =
2 3 2024
1 1 1 1
1 1 1 ..... 1
2 2 2 2
2 3 4 2024
2 3 2023
3 2 1 2 1 2 1 2 1
. . . ....
2 2(2 1) 2(2 1) 2(2 1) 2(2 1)
2024 2024
2023 2024 2024
3 2 1 2 1 3
. 3. 3 3
2 2 2 2

0.25
0.5
0.75
0.25
1
2
1
O
I
M
N
H
B
C
A
D
E