PHÒNG GD&ĐT HIỆP HÒA
(Đề chính thức)
ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN
Năm học: 2023 - 2024
Môn thi: TOÁN 8
Ngày thi: 27/01/2024
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Câu 1 (5,0 điểm):
1) Phân tích đa thức sau thành nhân tử
a)
2
2 21A x xy y=+ +−
b)
( ) ( ) ( )
2 22
Pxyz yzx zxy= −+ −+ −
2) Đa thức
( )
fx
khi chia cho
1x+
dư
1−
và chia cho
21x+
dư là
. Tìm đa thức dư
khi
( )
fx
chia cho
( )
( )
2
11xx++
.
3) Cho
,,abc
là các số hữu tỉ khác 0 thỏa mãn
a b c abc++=
. Chứng minh rằng biểu thức
( )( )( )
222
111Qabc=+++
là bình phương của một số hữu tỉ.
Câu 2(4,0 điểm):
1) Cho biểu thức
( )
33
22
2
1 1 51
11 1
1
xx x
A xx
x x xx
xx


−+

= + − −−


−+ −

−

. Tìm giá trị nhỏ nhất
của
A
khi
3x≥
.
2) Tìm
x
thỏa mãn
( )
( )
22
21 10x xx+− +=
.
Câu 3( 4,0 điểm):
1) Cho
2023
số nguyên dương phân biệt
1 2 2023
; ;...;aa a
lớn hơn 1.CMR tích
( )( ) ( )
22 2
1 2 2023
1 1 ... 1aa a++ +
ko chia hết cho tích
( )
2
1 2 2023
...aa a
.
2) Tìm tất cả các cặp số nguyên (x, y) thoả mãn
22
2 3 33110x y xy x y++ −−+=
.
Câu 4 (6 điểm):
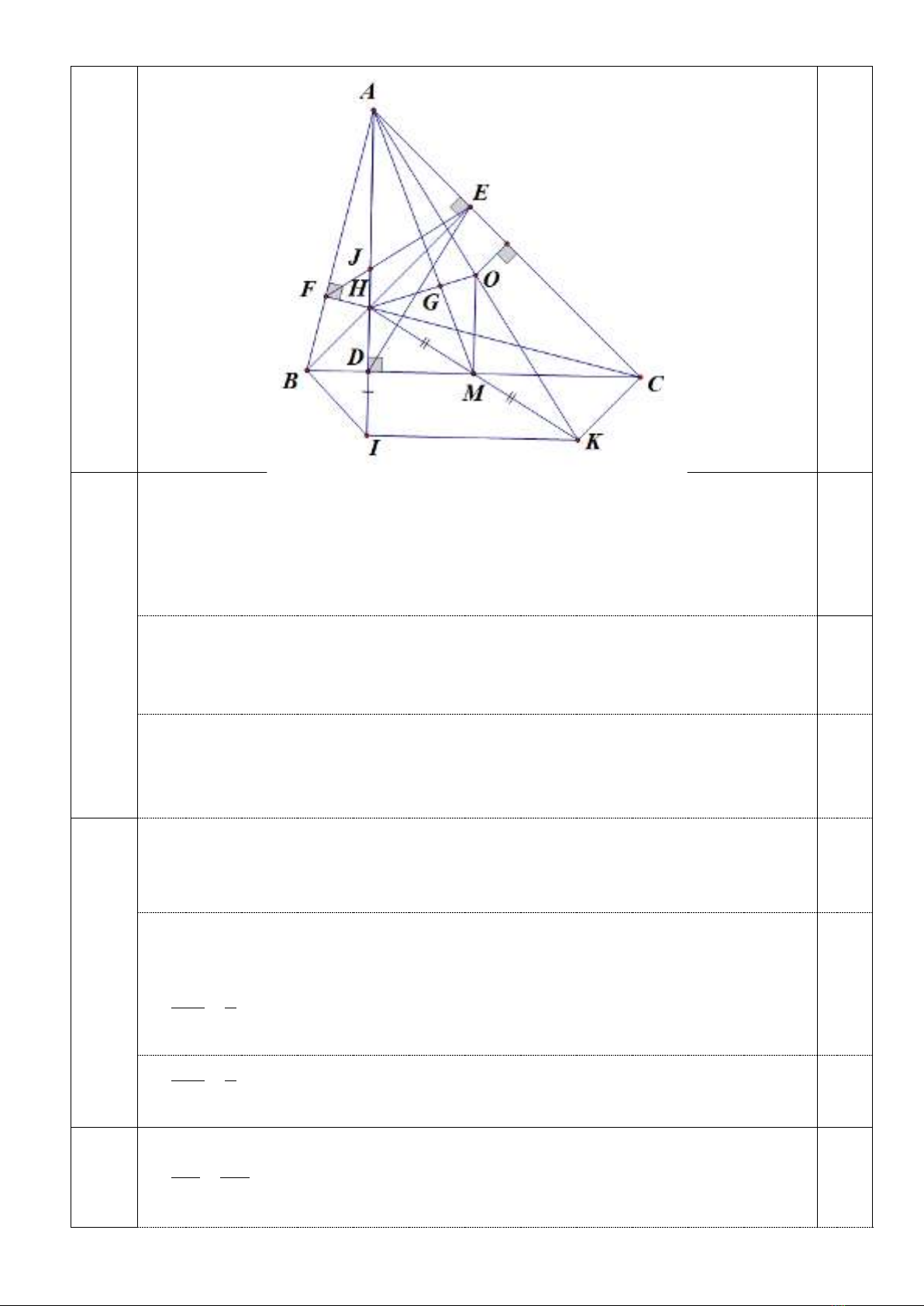
1) Cho tam giác nhọn
ABC
có đường cao
,,AD BE CF
và trực tâm
H
. Gọi
M
là trung
điểm của
BC
,
K
là điểm đối xứng với
H
qua
M
,
I
là điểm đối xứng với
H
qua
BC
.
a) Chứng minh rằng tứ giác
BIKC
là hình thang cân.
b) Kẻ trung trực của đoạn thẳng
AC
cắt
AK
tại
O
. Các đường thẳng
AM
và
HO
cắt nhau
tại
G
. Chứng minh
G
là trọng tâm của tam giác
ABC
.
c) Gọi
J
là giao điểm của
EF
và
AH
. Chứng minh rằng: EB là tia phân giác của
FED
, và
=AJ .HD AD.HJ
.
2) Cho tam giác
ABC
vuông tại
A
. Hình chữ nhật
MNPQ
thay đổi thỏa mãn
M
thuộc
cạnh
AB
,
N
thuộc cạnh
AC
và
,PQ
thuộc cạnh
BC
. Gọi giao điểm của
BN
với
MQ
là
K
,
của
CM
và
NQ
là
L
. Chứng minh rằng:
.KAB LAC=
Câu 5 (1 điểm):
Cho
,,abc
là các số thực dương. Chứng minh rằng
( ) ( ) ( )
22 22 2 2 2 2 2
1 1 1 111
222
111
ab bc ca abc
+ + ≤++
++ ++ ++ +++
.
.................... Hết.................
Họ và tên thí sinh:.........................................; Số báo danh...............................
HDC ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN
NĂM HỌC 2022-2023
Môn thi: Toán 8
Bài
Nội dung
Điể
m
1.1
(1,5đ)
a)
2
2 21A x xy y=+ +−
( )( ) ( )
1 12 1x x yx= − ++ +
( )( )
1 21x xy=+ +−
0,5
b)
( ) ( ) ( )
2 22
Pxyz yzx zxy= −+ −+ −
( )
2 2222
x y z yz yx zx zy= −+ − + −
( ) ( ) ( )( )
2
xyz yzyz xyzyz= −+ −− − +
0,5
( )
( )
2
y z x yz xy xz=− +−−
( ) ( ) ( ) ( )( )( )
yzxxy zxy yzxyxz= − − − − = − − −

0,5
1,2
(2,0đ)
Đa thức
( )
( )
2
11xx++
bậc là
3
nên dư của
( )
fx
chia cho
( )
( )
2
11xx++
có
dạng
2
ax bx c++
Do đó
( ) ( )
( )
( )
22
11 ,f x x x g x ax bx c x= + + + + +∀
0,5
Ta có
( ) ( )
( )
( )
22
11f x x x g x ax bx c=+ + + ++
( )
( )
( )
22
11x x g x ax a a bx c= + + + +−+ +
( )
( ) ( )
211x x g x a bx a c= + + + + − +

0,5
Nên
( )
fx
chia cho
2
1x+
dư là
bx a c−+
.
Do đó
3bx a c x x−+= ∀
hay
33
0
bb
ac ac
= =

⇔

−= =

(1) 0,5
Lại có
( )
fx
khi chia cho
1x+
dư
1−
nên
( )
11f−=−
hay
1abc−+=−
(2)
Từ (1) và (2) ta có
3
1
b
ac
=
= =
.
Vậy đa thức dư khi
( )
fx
chia cho
( )
( )
2
11xx++
là
231xx++
.
0,5
1.3
(1,5đ)
Với
,,abc
là các số hữu tỉ khác 0. Ta có:
a b c abc++=
111
1
ab bc ca
⇒++=
22
1111 1
1
a ab bc ca a
⇔+++=+
2
2
11 11 1a
ab ac a
+

⇔+ +=


0,5
22
11 11
1aa
ab ac

⇒ += + +


Tương tự ta có:
22
11 11
1bb
ab bc

+= + +


22
11 11
1cc
ac cb

+= + +


0, 5
( )( )( )
( )
222
2
222
11 11 11
111a b c abc ab bc ca
 
⇒ + + += + + +
 
 
0,5
Mà
,,abc∈
nên biểu thức
( )( )( )
222
111Qabc=+++
là bình phương của một
số hữu tỉ.
2.1
(2đ)
Ta có:
( )
33
22
2
1 1 51
11 1
1
xx x
A xx
x x xx
xx


−+

= + − −−


−+ −

−

( )
( )
( )
( ) ( ) ( )
( )
2
2 2 222
2
2
1 1 1 1 51 1
11 1
x xx x xx x x x
xx
xx
xx

− ++ + −+ − − − −

= + −⋅
−+
 −

( )( ) ( )
2424
22
2
2
512
12 12
1
xxxx
xx xx
xx
−+ −−+
=++ −+ ⋅ −
0,5
( ) ( ) ( ) ( )
2
22
22
4
11 11
x
xx
xx x
+
=+ −⋅−+
2
4x
x
+
=
Vậy
2
4x
Ax
+
=
0,5
Ta có
2
4 495x
A xx
xx x x
+
= = += +−
.
Do
3x≥
nên áp dụng bđt AM- GM cho các số dương ta được
99
2. . 6xx
xx
+≥ =
, dấu “=” xảy ra khi
3x=
( thỏa mãn )
0,5
Lại có
55 5 5
333
xxx
≥ ⇒ ≤ ⇒− ≥−
Do đó
5 13
633
A≥−=
.
Dấu “=” xảy ra khi
3x=
.
Vậy Min
13
3
A=
tại
3x=
.
0,5
2.2
(2đ)
Ta có
( )
( )
22
2
1 10x xx+− +=
( ) ( )
2
22
12 10x x xx

⇔ +− − +=

0,5
( ) ( )
42
2
15 14 0x xx x⇔+− ++ =
( ) ( ) ( )
42 2
2
1 14 14 0x xx xx x⇔+− +− ++ =
( ) ( ) ( )
22 2
1 1 41 0xxxxxx

⇔+ +−− +−=

0,5
( ) ( )
22
1 14 0x xx x

⇔ +− +− =

( )
( )
2
2
1 10xx x⇔ ++ − =
0,5
( )
2
10x⇔− =
( do
210xx x+ +>∀
)
1x⇔=
. Vậy
1x=
.
0,5
3.1
(2đ)
Ta xét
( )( ) ( )
( )
22 2
1 2 2919
2
1 2 2019
1 1 ... 1
. ...
aa a
Aaa a
++ +
=
2
22
2019
12
22 2
1 2 2019
1
11
. ... a
aa
Aaa a
+
++
=
0,5
Do
2023
số nguyên dương phân biệt
1 2 2023
; ;...;aa a
lớn hơn 1 nên ta gỉa sử
1 2 2023
2 ...aa a≤ < <<
.
Do đó
1 2 3 2023
2 ;3 ;4 ;...;2024aa a a≤≤ ≤ ≤
.
Ta có
2 22
1
2 222
1 11
1 1 1 22
11
1 2 1 1.3
a
a aa
+=+ <+ ≤ =
−−
.
0,5
Tương tự
222
2
2 2 22
2 22
11 1 33
11
1 3 1 2.4
a
a aa
+=+ <+ ≤ =
−−
…
Do đó
2
22 22 2
2023
12
22 2
1 2 2023
1
11 2 .3 ...2023 2023.2
1 . ... 2
1.3.2.4...2022.2024 2024
a
aa
Aaa a
+
++
<= < = <
0,5
A⇒
không nguyên.
⇒
( )( ) ( )
22 2
1 2 2023
1 1 ... 1aa a++ +
ko chia hết cho
( )
2
1 2 2023
...aa a
. 0,5
3.2
(2đ)
22
2 3331102()()3()110x y xy x y xxy yxy xy++ −−+=⇔ ++ +− ++=
( )(2 3) 11xy xy⇔ + +− =−
0,5
Vì
,xy Z x y∈⇒+
và
23xy+ −∈
Ư(11)
Ta có 4 trường hợp sau:
Trường hợp 1:
11 9
2 3 1 20
xy x
xy y
+= =−

⇔

+−=− =

.
0,5
Trường hợp 2:
1 15
2 3 11 16
xy x
xy y
+=− =

⇔

+−= =−

.
Trường hợp 3:
11 15
2 3 1 26
xy x
xy y
+=− =

⇔

+−= =−

.
0,5
Trường hợp 4:
19
2 3 11 10
xy x
xy y
+= =−

⇔

+−=− =

.
Vậy tất cả các cặp số nguyên (x, y) là (–9; 20), (15; –16), (15; – 26), ( –9; 10).
0,5
4,1
(4,5đ)
1.a
(1,5đ)
Có
H
đối xứng với
K
qua
M
MH MK⇒=
H
đối xứng với I qua
BC
DH DI⇒=
⇒
DM
là đường trung bình của
IKH∆
⇒
DM / / IK
⇒
BC / / IK
⇒
Tứ giác
BIKC
là hình thang. (1)
0,5
Có tứ giác
BHCK
là hình bình hành (do
M
vừa là trung điểm của
BC
vừa là
trung điểm của
HK
)
BH / / KC⇒
MCK MBH⇒=
(so le trong)
0,5
Mà
MBH MBI=
(do
BC
là trung trực của
HI
)
MBI MCK⇒=
(2)
Từ (1) và (2)
BIKC⇒
là hình thang cân.
0,5
1.b
(1,5đ)
Tứ giác
BHCK
là hình bình hành
BH / / KC⇒
hay
HE / / KC
,
Mà
HE AC⊥
(
BE
là đường cao của tam giác
ABC
)
HE⇒
song song với đường trung trực của
AC
0, 5
KC⇒
song song với đường trung trực của
AC
⇒
O
là trung điểm của
AK
.
⇒
OM
là đường trung bình của
AHK∆
1
2
OM
AH
⇒=
và
OM / / AH
AHG OMG⇒∆ ∆฀
0, 5
1
2
GM
AG
⇒=
mà
AM
là đường trung tuyến của tam giác
ABC
.
⇒
G
trọng tâm của tam giác
ABC
.
0,5
1.c
(1,5đ)
Ta có
AEB AFC∆∆฀
(gg)
AF AC
AE AB
⇒=
AEF ABC⇒∆ ∆฀
(c.g.c)
0,5