TR¦êNG §¹I HäC VINH
TR¦êNG THPT CHUY£N
§Ò THI KHAO SÁT CHẤT LƯỢNG ĐẦU N¡M
năm học: 2012 - 2013
M«n: To¸n - Líp 12; Thêi gian lµm bµi: 120 phót
Câu 1. (3 điểm) Cho hàm số x
x
y−
−
=2
32 có đồ thị
(
)
C.
a, Tìm điểm M thuộc
()
C biết hoành độ của nó thoả mãn phương trình
()
2''
=
xy .
b, Viết phương trình tiếp tuyến với đồ thị
(
)
C tại điểm M tìm được ở câu a.
Câu 2. (2 điểm)
a, (1 điểm) Cho hàm số
()()
32123
3
123 +−+−+= xmxmxy , m là tham số. Tìm
m để hàm số đạt cực tiểu tại điểm 1
=
x.
b, (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
()
2
42 xxy −+= .
Câu 3. (1 điểm) Giải hệ phương trình
⎪
⎩
⎪
⎨
⎧
=−+−
−+++=++−
0532
2737312
2
23223
xxyx
yxyxxxyxy .
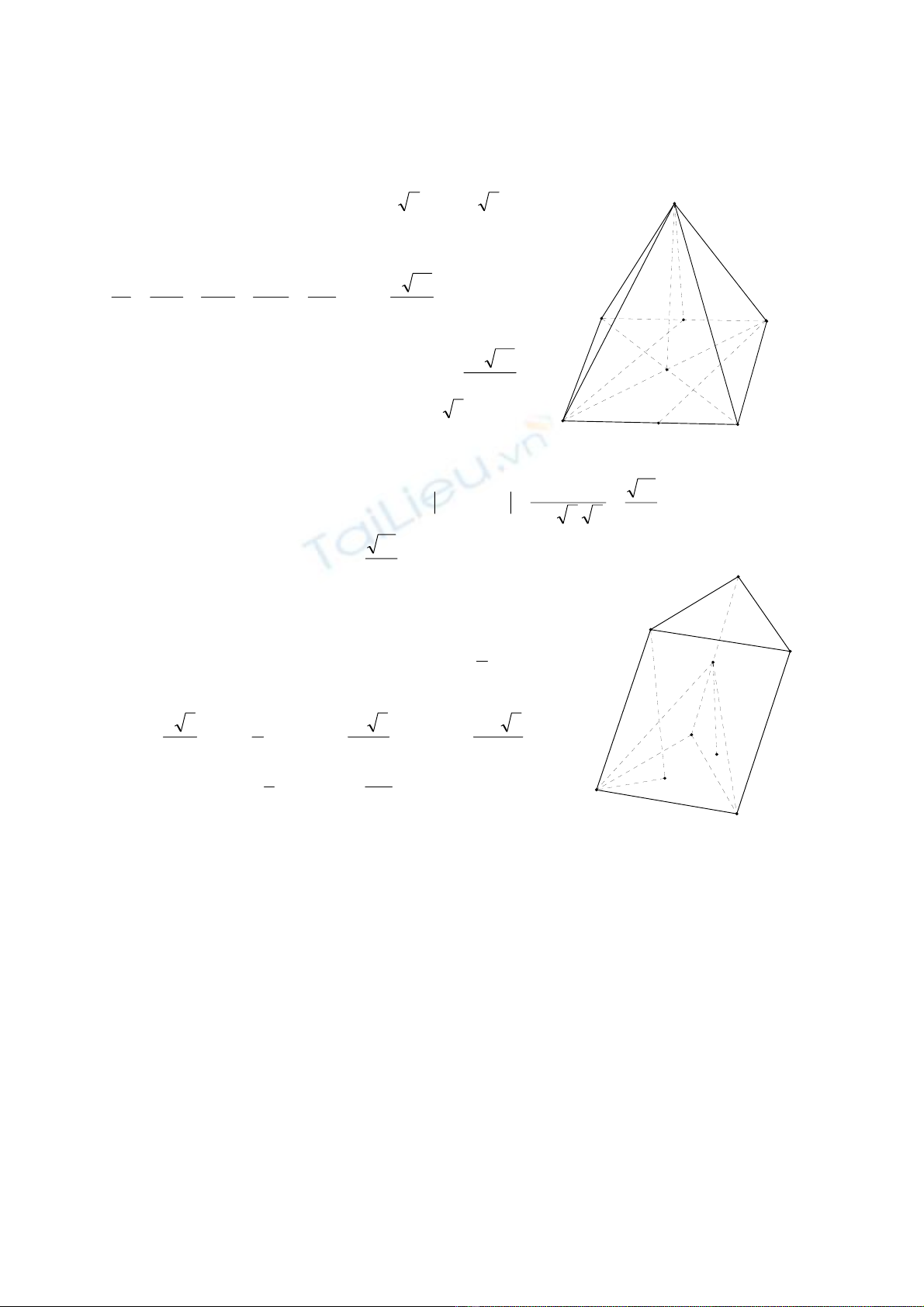
Câu 4. (3 điểm) Cho hình chóp tứ giác đều S.ABCD có cạnh bên gấp3 lần cạnh
đáy.
a, Cho 2aAB =. Tính khoảng cách giữa hai đường thẳng AD và SC.
b, Gọi M là trung điểm AB. Tính góc giữa hai đường thẳng SA và CM.
Câu 5. (1 điểm) Cho hình lăng trụ tam giác ABC. A’B’C’ có đáy là tam giác đều,
cạnh bên bằng a và tạo với đáy một góc 0
60 . Gọi D là trung điểm cạnh CC’. Biết
rằng hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với trọng tâm tam
giác ABC. Tính thể tích khối tứ diện ABCD.
.…………Hết………….
TR¦êNG §¹I HäC VINH
TR¦êNG THPT CHUY£N
ĐÁP ÁN §Ò THI KSCL ĐẦU N¡M
Năm học: 2012 - 2013
M«n: To¸n - Líp 12; Thêi gian lµm bµi: 120 phót
Câu 1. (3 điểm) TXĐ
{}
2\RD =.
a, (1,5 điểm)
() ()
2
2
1
'x
xy −
=,
() ()
3
2
2
'' x
xy −
=
Theo giả thiết ta có
() ()
1122
2
23
3=⇔=−⇔=
−xx
x.
Suy ra điểm M cần tìm là:
(
)
1;1
−
M.
b, (1,5 điểm) Tại
()
1;1 −M, hệ số góc của phương trình tiếp tuyến là
()
11'
=
y
Phương trình tiếp tuyến cần tìm là: 2
−
=
xy .
Câu 2. (2 điểm)
a, (1 điểm) TXĐ
R
.
Ta có:
() ( )
mxmxxy 21232' 2−+−+= ,
(
)
462''
−
+
=
mxxy .
Hàm số đạt cực tiểu tại điểm 1
=
x khi:
()
()
2
1
026
024
01''
01' =⇔
⎩
⎨
⎧
>−
=−
⇔
⎩
⎨
⎧
>
=m
m
m
y
y.
b, (1 điểm) TXĐ
[]
2;2−=D.
Ta có
()
2
2
4
224
'x
xx
xy −
−−
=
()
⇔= 0' xy 10
4
224
2
2
=⇔=
−
−− x
x
xx
Vì
()
(
)()
331,02,02 ===− yyy .
Suy ra: GTLN của hàm số là 33 , GTNN của hàm số là 0.
Câu 3. (1 điểm) Ta có: 2737312 23223 −+++=++− yxyxxxyxy
()
(
)
(
)
(
)
1212 33 −+−=−+−⇔ xxyxyx
Xét hàm số tttf += 3
)( trên
R
, phương trình trên có dạng
()( )
12
−
=− xfyxf
Vì
()
Rtttf ∈∀>+= ,013' 2 nên hàm số
(
)
tf đồng biến trên
R
.
Do đó
()( )
12 −=− xfyxf xyxyx
−
=
⇔
−
=
−
⇔112 .
Thế vào phương trình còn lại ta được: ⎢
⎢
⎣
⎡
−=
=
⇔=−+
3
5
1
0523 2
x
x
xx .
Hệ đã cho có hai nghiệm
()
yx, là
(
)
0,1 và ⎟
⎠
⎞
⎜
⎝
⎛−3
8
,
3
5.
Câu 4. (3 điểm)
a, (1,5 điểm) 5,6,2 aSOaSAaAC === .
Đặt
()
)(; SBCOdh =
Suy ra
11
55
5
111111
22222
a
h
aOCOBOSh =⇒=++= .
Ta có
()( )( )
11
552
2)(;2)(;; a
hSBCOdSBCAdSCADd ==== .
b, (1,5 điểm) Đặt 322 =⇒= SAAB
Gọi N là trung điểm của CD
11,5 22 ==⇒ SNAN
Ta có
()()
10
15
5.32.2
11512
cos,cos,cos =
−+
=∠== SANANSACMSA .
Suy ra
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=10
15
arccos,CMSA .
Câu 5. (1 điểm) Gọi H, K lần lượt là hình chiếu A’, D
lên (ABC).
Suy ra H là trọng tâm ABCΔvà .'
2
1HADK =
.
16
33
16
3
2
,
2
3
'
22 a
S
a
S
a
AH
a
HA ABCHAB =⇒=⇒== ΔΔ
Vậy .
64
3
.
3
13
a
SDKV ABCABCD == Δ
O
S
D
B
C
N
M
a
A
'
A
C'
B'
B
C
H
K
D