Đề thi thử Đại học và đáp án môn Toán năm 2009 - Bám sát cấu trúc của Bộ Giáo Dục (ĐỀ 01)

Đề thi thử Đại học năm 2009 Bám sát cấu trúc của Bộ Giáo Dục

ĐỀ 01

Thi vào thứ hai hàng tuần tại A7 Bà Triệu – Đà Lạt

I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH ( 7,0 điểm )

Câu I : ( 2 điểm ) Cho hàm số :

3 2

3 4

y x x

   





1

1.

Khảo sát sự biến thiên và vẽ đồ thị hàm số





1

.

2.

Với giá trị nào của

m

thì đường thẳng nối hai cực trị đồ thị của hàm số





1

tiếp xúc với đường tròn





 





2

: 1 5

C x m y m

    

.

Câu II: ( 2 điểm )

1.

Giải phương trình :

5 1

5 2 5

2 2

x x

   

2.

Giải phương trình :





 

2

3 2cos cos 2 sin 3 2cos 0

x x x x

    

.

Câu III: ( 1 điểm ) Tính giới hạn :

 

1

cos6

4

limln 1 cos2

x

xx



.

Câu IV: ( 1 điểm ) Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông tâm

O

, cạnh bằng

a

,





SA ABCD

 và

2

SA a

. Gọi

H

và

K

lần lượt là hình chiếu của

A

trên

SB

và

SD

. Giả sử

N

là giao

điểm của đường thẳng

SC

và





AHK

. Chứng minh rằng

AN HK



và tính thể tích khối chóp

.

S AHNK

.

Câu V: ( 1 điểm )

Cho

3

số thực dương

, ,

a b c

.Chứng minh rằng :

 

     

3 3 3

1

2

a b c

b c a c a b a b c

    

  

II. PHẦN RIÊNG ( 3,0 điểm )

Thí sinh chỉ được làm một trong hai phần ( phần 1 hoặc 2 ).

1.

Theo chương trình Chuẩn :

Câu VI.a ( 2 điểm )

1.

Viết phương trình mặt phẳng qua giao tuyến của

2

mặt phẳng





: 4 5 0

P x y

  

và





: 3 2 0

Q x y z

   

, đồng thời vuông góc với mặt phẳng





: 2 7 0

R x z

  

2.

Tìm trên giao tuyến của hai mặt phẳng









,

P Q

ở câu

1

những điểm

M

sao cho khoảng cách từ

M

đến mặt

phẳng





: 2 2 7 0

S x y z

   

một khoảng bằng

2

?.

Câu VII.a ( 1 điểm ) Cho tập





0;1;2;3;4;5

A

,từ

A

có thể lập được bao nhiêu số tự nhiên gồm

5

chữ số khác

nhau ,trong đó nhất thiết phải có mặt chữ số

0

và

3

?.

2.

Theo chương trình Nâng cao :

Câu VI.b ( 2 điểm )

1.

Viết phương trình mặt phẳng





P

qua

O

,vuông góc với mặt phẳng





: 0

Q x y z

  

và cách điểm





1;2; 1

M



một khoảng bằng

2

.

2.

Cho hai đường thẳng

 

1

3 7

: 1 2

1 3

x t

d y t

z t



 



 





 





và

 

2

7

: 3 2

9

x u

d y u

z u



 



 



 





.Lập phương trình đường thẳng





d

đối xứng

với đường thẳng





1

d

qua





2

d

.

Câu VII.b ( 1 điểm ) Cho số phức

1 3

z i

  . Hãy viết dạng lượng giác của số phức

5

z

.

GV ra đề : Nguyễn Phú Khánh – A7 Bà Triệu Đà Lạt , 42B/11 Hai Bà Trưng Đà Lạt .

Đề thi thử Đại học năm 2009 Bám sát cấu trúc của Bộ Giáo Dục

Đáp án đề thi

I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH ( 7,0 điểm )

Câu I : ( 2 điểm ) Cho hàm số :

3 2

3 4

y x x

   





1

1.

Khảo sát sự biến thiên và vẽ đồ thị hàm số





1

. Học sinh tự làm .

2.

Với giá trị nào của

m

thì đường thẳng nối hai cực trị đồ thị của hàm số





1

tiếp xúc với đường tròn





 





2

: 1 5

m

C x m y m

    

.

Đồ thị hàm số





1

có cực tiểu





2;0

A

 , cực đại





0;4

B

. Phương trình đường thẳng nối hai cực trị của hàm số





1

là

   

: 1 : 2 4 0

2 4

x y

AB AB x y

     

.





m

C

có tâm





; 1

m

I m m



, bán kính

5

R

.

Đường thẳng





AB

tiếp xúc với đường tròn





m

C

khi

 

,2

2

3 5 2

2 1 4 5 3 5

3 5 8

2 1

m

I AB

m m

d R m m m

  

 

  

       

 

    

   

  .

Câu II: ( 2 điểm )

1.

Giải phương trình :

5 1

5 2 5

2 2

x x

   

Điều kiện :

0

x



Bất phương trình cho viết lại :

 

1 1

5 2 5 1

2 4

x x

   

   

 

   

 

Đặt :

 

1

2 2 , 0

2

t x do x

x

   

.

Khi đó

 

2 2

1 1

2 1 1

4 4

t x x t

x x

       

Phương trình

 

2 2

1

1 5 2 1 5 2 5 3 0

3

2

t

t t t t t







         







Điều kiện

2

t

 , do đó

3

2

t



Khi đó

 

2

1

1 3

1

2

2 3 1 0 0

2 2

4

21

01

00

x

x xx x

xx







   

 

   



   

   





  











Vậy tập nghiệm của bất phương trình cho là :





1

0; 1;

4

T 

  



 

2.

Giải phương trình :





   

2

3 2cos cos 2 sin 3 2cos 0 1

x x x x

    

 





2

1 2 3 1 sin 3 cos 2 3 3.sin 2sin .cos 0

x x x x x

      

2

2 3 sin 3.sin 3 cos 2sin .cos 0

x x x x x

     









3.sin 2sin 3 cos 3 2sin 0

x x x x

     









3 2sin 3.sin cos 0

x x x

   

Đề thi thử Đại học năm 2009 Bám sát cấu trúc của Bộ Giáo Dục

 

31sin sin

3 2sin 0 32 3

1

3.sin cos 0 t n t n 6

3 6

n

x n nx

x

x x x k k

a x a

 





  

   

   

  

 



   

       



   

 



 





Câu III: ( 1 điểm ) Tính giới hạn :

 

1

cos6

4

limln 1 cos2

x

xx





Dễ thấy

   





 





 

1

cos6

ln 1 sin 2

sin 2

12

2

ln 1 cos2 .ln 1 cos2 .

cos6 cos3 2 sin 2

2

x

x x

x x x



 

 



 

 

   



 

   





 





 

3 2

ln 1 sin 2 ln 1 sin 2

cos 2 1

2 2

. .

4cos 2 3cos 2 4cos 2 3

sin 2 sin 2

2 2

x x

x

x x x

x x

 

   

   

   

   

 

 

   





 

1

cos6 2

4 4

ln 1 sin 2

1 1

2

limln 1 cos2 lim .

4cos 2 3 3

sin 2

2

x

x x

x

xxx

 



 

 

 

 

 

   



Cách 2 : Đặt

, 0

4 4

t x x t

 

    

   









1

cos6 0

4 4

ln 1 sin2

1

limln 1 cos2 lim .ln 1 cos2 lim

cos6 sin6

xt

x x

t

x x

x t

 



 

 

   

 

 

 

   

 

 





0 0

sin2

.2

ln 1 sin2 ln 1 sin2

sin2 1

2

lim . lim . sin6

sin2 sin6 sin2 3

6

t t

t

t t

ttt

t t t

t

 



   



   

 

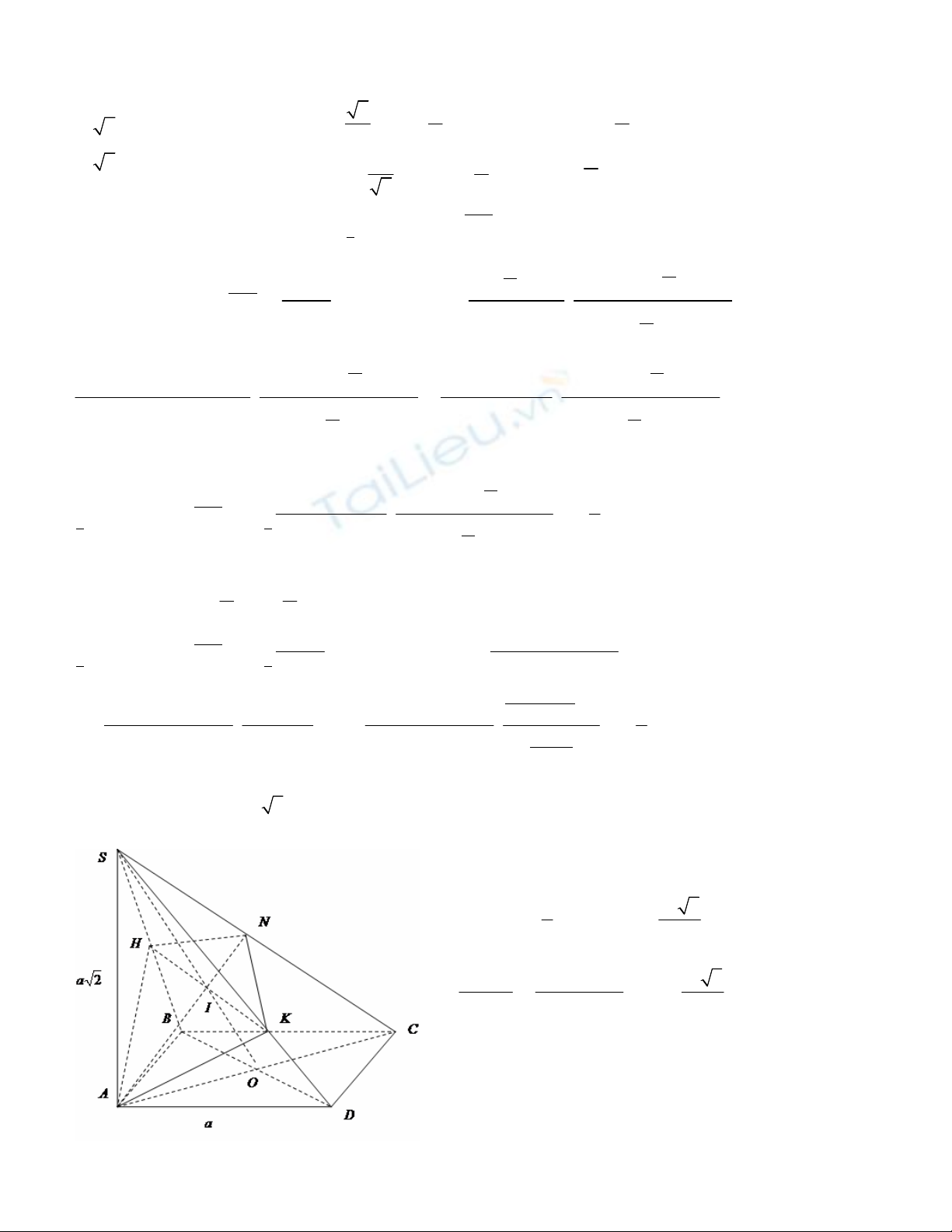
Câu IV: ( 1 điểm ) Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông tâm

O

, cạnh bằng

a

,





SA ABCD

 và

2

SA a

. Gọi

H

và

K

lần lượt là hình chiếu của

A

trên

SB

và

SD

. Giả sử

N

là giao

điểm của đường thẳng

SC

và





AHK

. Chứng minh rằng

AN HK



và tính thể tích khối chóp

.

S AHNK

.

Chứng minh tứ giác

AHNK

có

2

đường chéo vuông góc

là

AN HK



3

.

1 2

.

3 9

S AHNK AHNK

a

dt dt SN  (đvtt).

Hoặc dùng tỷ số thể tích : 3

. . 2

...

. . 9

SAHNK

ABCD

V SH SN SK a

V SB SC SD

   (đvtt)

Đề thi thử Đại học năm 2009 Bám sát cấu trúc của Bộ Giáo Dục

Câu V: ( 1 điểm )

Cho

3

số thực dương

, ,

a b c

.Chứng minh rằng :

 

     

3 3 3

1

2

a b c

b c a c a b a b c

    

  

Phân tích bài toán :



Đẳng thức cần chứng minh đưa về dạng :

 

3 3 3

0

a b c

m a c nb k b a pc i b c ja

b c a c a b a b c

           

   .



Giả sử

0

a b c

  

. Dự đoán đẳng thức xảy ra khi

a b c

 

.

Từ đó gợi mở hướng giải :

 

3

a

m a c nb mna

b c a

   

. Đẳng thức xảy ra khi

   

33

1

4

1

2

am

m a c nb a

b c a m a a na

a a a

a b c n





   

    

 



 

 





Tương tự cho các trường hợp khác .

Giải :

   

3

1 1 3

2 4 2

a

b c a a

b c a

   

. Đẳng thức xảy ra khi:

   

3

1 1

2 4

a

b c a

  

.

   

3

1 1 3

2 4 2

b

c b a b

c a b

   

. Đẳng thức xảy ra khi:

   

3

1 1

2 4

b

c b a

c a b

  

.

   

3

1 1 3

2 4 2

c

a b c c

a b c

   

. Đẳng thức xảy ra khi:

   

3

1 1

2 4

c

a b c

  

.

Cộng vế theo vế ta được :

 

     

3 3 3

1

2

a b c

b c a c a b a b c

    

   .

Dấu đẳng thức xảy ra khi :

0

a b c



II. PHẦN RIÊNG ( 3,0 điểm )

Thí sinh chỉ được làm một trong hai phần ( phần 1 hoặc 2 ).

1.

Theo chương trình Chuẩn :

Câu VI.a ( 2 điểm )

1.

Viết phương trình mặt phẳng qua giao tuyến của

2

mặt phẳng





: 4 5 0

P x y

  

và





: 3 2 0

Q x y z

   

, đồng thời vuông góc với mặt phẳng





: 2 7 0

R x z

  

.

Giả sử đường thẳng





d

là giao tuyến của

2

mặt phẳng





P

và





Q

nên phương trình đường thẳng





d

có dạng

 

4 5 0

:

3 2 0

x y

dx y z

  







   





hay

 

5 4

:13 13

x t

d y t t R

z t

 



 



  









d

đi qua điểm





5;0; 13

M

 và có vtcp





4;1;13

u

 



, mặt phẳng





R

có vtpt





2;0; 1

R

n

 



.

Mặt phẳng cần tìm đi qua điểm





5;0; 13

M

có vtpt là









; 1;22; 2

R

n u n

  

  

nên phương trình có dạng













1 5 22 0 2 13 0 22 2 21 0

x y z x y z

           

.

Chú ý : Bài toán này có thể giải theo dạng chum mặt phẳng , tuy nhiên phương pháp này không đề cập trong

chương trình mới hiện nay .

Đề thi thử Đại học năm 2009 Bám sát cấu trúc của Bộ Giáo Dục

2.

Tìm trên giao tuyến của hai mặt phẳng









,

P Q

ở câu

1

những điểm

M

sao cho khoảng cách từ

M

đến mặt

phẳng





: 2 2 7 0

S x y z

   

một khoảng bằng

2

?.

Giao tuyến của hai mặt phẳng









,

P Q

là

 

5 4

:13 13

x t

d y t t R

z t

 



 



  













5 4 ; ; 13 13 ,

M d M t t t t R

     

.

 





 





   

;2 2

2

2 5 4 2 13 13 7

30 23

5

2 2 1

M S

t t t

t

d      

 

   

Theo bài toán

 

;

20 20

, ; ;

30 23 10

30 23

23 23

2 2 30 23 10 30 23 10

40 40

5

, ; ;

23 23

M S

t M

t

d t tt M



 



 

  





 

        

  

 





 



 



Câu VII.a ( 1 điểm ) Cho tập





0;1;2;3;4;5

A

,từ

A

có thể lập được bao nhiêu số tự nhiên gồm

5

chữ số khác

nhau ,trong đó nhất thiết phải có mặt chữ số

0

và

3

?.

Cách 1: Gọi số tự nhiên có

5

chữ số khác nhau được lập từ tập

A

là:

1 2 3 4 5 1

, 0

a a a a a a



Số cách chọn

1

a

có

5

cách .Số cách chọn

2345

a a a a

là số chỉnh hợp chập

4

của

5

:

4

5

A

.Suy ra : có

4

5

5. 600

A



(số) .

Trong

600

số trên thì: Số không có chữ số

0

được lập từ tập





1;2;3;4;5

B

 là số chỉnh hợp chập

4

của

5

:

4

5

120

A

 (số).

Số không có chữ số

3

được lập từ tập





0;1;2;4;5

A

:Số cách chọn

1

0

a



có

4

cách. Số cách chọn

2345

a a a a

là số hoán vị

4

P

.Suy ra : có

4

4. 96

P



(số).

Vậy theo yêu cầu bài toán ta có :

600- (120 + 96) = 384

(số)

Cách 2:

Số cách chọn số tự nhiên gồm

5

chữ số khác nhau ,trong đó nhất thiết phải có mặt chữ số

0

và 3,chính là số

cách xếp

5

chữ số từ tập A vào

5

ô liên tiếp nhau.

Vì nhất thiết phải có mặt chữ số

0

và

3

nên ta chọn số

0

và

3

xếp trước

Vì số

0

không được đứng ở vị trí đầu tiên nên có

4

cách xếp.

Số

3

có

4

cách xếp vào

4

vị trí còn lại.Số cách xếp

3

số còn lại chính là số chỉnh hợp chập

3

của

4

:

3

4

A

.

Vậy theo yêu cầu bài toán ta có :

3

4

4.4 384

A

 (số).

2.

Theo chương trình Nâng cao :

Câu VI.b ( 2 điểm )

1.

Viết phương trình mặt phẳng





P

qua

O

,vuông góc với mặt phẳng





: 0

Q x y z

  

và cách điểm





1;2; 1

M



một khoảng bằng

2

.

Mặt phẳng





P

qua

O

nên có phương trình:





2 2 2

: 0, 0

P ax by cz a b c

     

, vtpt :





; ; 0

n a b c

 





Mặt phẳng





Q

có vtpt





1;1;1

m





. Vì









P Q

nên





. 0 0 1

n m n m a b c

      

   

.

Đề thi thử Đại học và đáp án môn Toán năm 2009 - Bám sát cấu trúc của Bộ Giáo Dục (ĐỀ 01)

Tham khảo tài liệu 'đề thi thử đại học và đáp án môn toán năm 2009 - bám sát cấu trúc của bộ giáo dục (đề 01)', tài liệu phổ thông, ôn thi đh-cđ phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi