TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG ĐỀ THI THỬ ĐẠI HỌC (LẦN 1)
Năm học: 2013-2014 Môn: TOÁN; Khối A và khối A1
Thời gian: 180 phút (không kể thời gian phát đề)
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu 1 ( 2,0 điểm). Cho hàm số
2x 3
y
x 2
có đồ thị (C).
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (C)
b) Tìm trên (C) những điểm M sao cho tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) tại A, B sao cho AB
ngắn nhất .
Câu 2 ( 1,0 điểm). Giải phương trình:
2sin 2x +sinx+3cosx+2=0
4
Câu 3 ( 1,0 điểm). Giải bất phương trình:
2 3 2
5
x 2 log 2 x x 2 1 x 6 3x x
Câu 4 ( 1,0 điểm). Giải hệ phương trình: 3 3 2
2 2 2
3 3 2 0
1 3 2 1 0
x y y x
x x y y
Câu 5 ( 1,0 điểm). Cho hình chóp
S.ABC
, có đáy ABC là tam giác vuông tại A,
·
0
AB a, ACB 30
. Gọi I là
trung điểm BC, hình chiếu vuông góc của điểm S lên mặt đáy (ABC) là điểm H thỏa mãn:
IA 2IH
uur uur
. Góc
giữa SC và mặt đáy (ABC) bằng
0
60
. Tính thể tích khối chóp S.ABC và tính khoảng cách từ trung điểm K của
SB tới mặt phẳng (SAH) theo a ?
Câu 6 ( 1,0 điểm). Cho ba số thực a, b, c thỏa mãn
1 2 3
a ; b ; c
2 3 4
và
2a 3b 4c 7

. Tìm giá trị nhỏ
nhất của biểu thức
1 1 1
A 2a 3b 4c
2a 1 3b 2 4c 3
II. PHẦN RIÊNG (3,0 điểm): Thí sinh chỉ được làm một trong hai phần (phần A hoặc phần B)
A. Theo chương trình chuẩn
Câu 7.a (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trực tâm
H(1; 1)
, điểm
M( 1;2)
là trung điểm AC và phương trình cạnh BC là:
2x y 1 0
. Xác định tọa độ các đỉnh A, B, C của
tam giác ABC ?
Câu 8.a (1,0 điểm). Cắt hình nón (N) đỉnh S cho trước bởi mặt phẳng qua trục của nó, ta được một tam giác
vuông cân có cạnh huyền bằng
a
2
. Tính diện tích xung quanh của hình nón (N). Tính thể tích khối cầu nội
tiếp hình nón (N)
Câu 9.a (1,0 điểm). Cho hai đường thẳng
1
d
và
2
d
cắt nhau tại điểm O. Trên
1
d
lấy 6 điểm phân biệt khác điểm
O. Trên
2
d
lấy n điểm phân biệt khác điểm O. Tìm n để số tam giác tạo thành từ
n 7
điểm trên (kể cả điểm O)
là 336
B. Theo chương trình nâng cao
Câu 7.b (1,0 điểm). Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): x + y – 2 = 0 cắt đường tròn (C) có
phương trình: 2 2
4 4 4 0
x y x y
tại hai điểm A và B. Tìm điểm C trên đường tròn (C) sao cho diện tích
tam giác ABC lớn nhất?
Câu 8.b (1,0 điểm). Cho hình trụ (T) có bán kính đáy bằng a. Một mặt phẳng
( )
song song và cách trục
'
OO
của hình trụ bằng
a
2
cắt hình trụ (T) theo thiết diện là hình vuông. Tính diện tích xung quanh của hình trụ (T)
và tính thể tích khối cầu ngoại tiếp hình trụ (T)
Câu 9.b (1,0 điểm). Một hộp đựng 4 viên bi xanh, 5 viên bi đỏ, 3 viên bi vàng. Chọn ngẫu nhiên 3 viên bi.
Tính xác suất để 3 viên bi được chọn, trong đó có đúng một viên bi xanh ?
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh: ……………………………………………; Số báo danh: …………………….
--------------------------------------------HẾT--------------------------------------------
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC (LẦN 1) KHỐI A VÀ A1 – Năm hoc: 2013-2014
Câu 1: (2,0 điểm)
a)(1,0 đ)
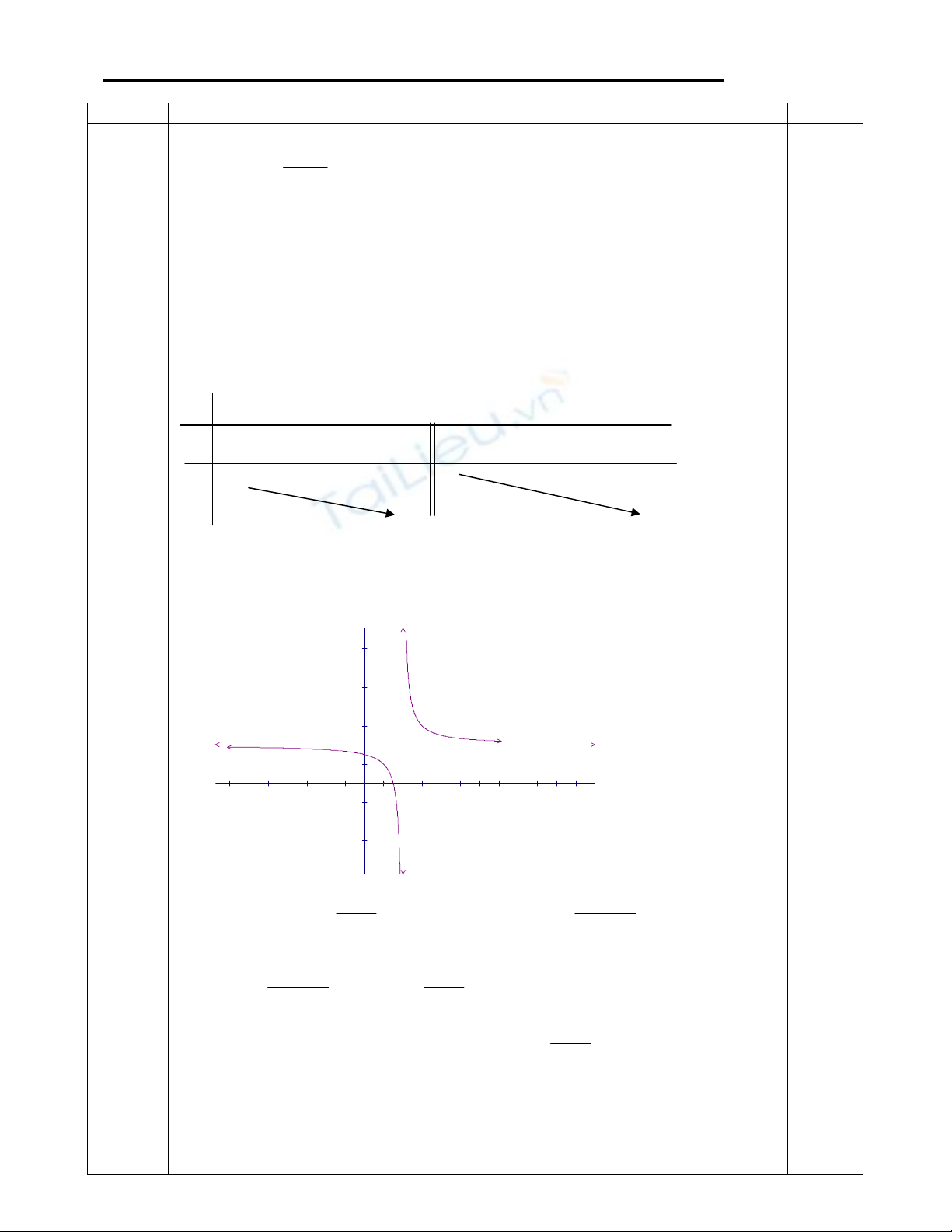
Hàm số y =
2x 3
x 2
- TXĐ: D =
R
\ {2}
- Sự biến thiên:
+ ) Giới hạn: x
lim y 2

. Do đó ĐTHS nhận đt y = 2 làm TCN
x 2 x 2
lim y ; lim y
 
. Do đó ĐTHS nhận đt x = 2 làm TCĐ ……………..
+) Bảng biến thiên:
Ta cã : y’ =
2
1
x 2
< 0
x D
..........................................................
Hàm số nghịch biến trên hai khoảng

;2
và

2; ,
hàm số không có cực trị ...............................................................................
+ ) Vẽ đồ thị
0,25
0,25
0,25
0,25
b)(1,0 đ) Lấy điểm 1
M m;2
m 2
C
. Ta có :
2
1
y' m
m 2
.
Tiếp tuyến (d) tại M có phương trình :
2
1 1
y x m 2
m 2
m 2
………………………………….
Giao điểm của (d) với tiệm cận đứng là : 2
A 2;2
m 2
Giao điểm của (d) với tiệm cận ngang là : B(2m – 2 ; 2) …………………..
Ta có :
2
22
1
AB 4 m 2 8
m 2
. .................................................
Dấu “=” xảy ra khi m = 1 hoặc m=3
0,25
0,25
0,25
8
6
4
2
-2
-4
-5
5
10
y’
y
x


-


2
-
2
2
2
Vậy điểm có hai điểm cần tìm 1
M (1;1)
và 2
M (3;3)
........................................ 0,25
Câu 2: (1,0 điểm)
2sin 2x +sinx+3cosx+2=0
4
2
sin 2x cos2x+sinx+3cosx+2=0 2sinx.cosx+2cos
x 1 sinx+3cosx+2=0
sinx(2cosx+1)+(2cosx+1)(cosx+1)=0
(2cosx+1)(sinx+cosx+1)=0
2cosx+1=0 (1)
(2cosx+1)(sinx+cosx+1)=0
sinx+cosx+1=0 (2)
……………….
*
2
x k.2
23
(1) 2cosx+1=0 cosx=cos (k )
32
x k.2
3
¢
……..
*x k.2
(2) sinx+cosx+1=0 sin x+ sin (k )
2
4 4 x k.2
¢
Vậy phương trình đã cho có nghiệm là:
2 2
x k.2 ; x k.2 ; x k.2 ; x k.2
3 3 2
……………..
0,25
0,25
0,25
0,25
Câu 3: (1,0 điểm)
1/ (1 đ)
2 3 2
5
x 2 log 2 x x 2 1 x 6 3x x
2 2
5
x 2 log 2 x x 2 1 x x 3 0
2 2
5
2 2
5
x 2 0
(I)
log 2 x x 2 1 x x 3 0
x 2 0
(II)
log 2 x x 2 1 x x 3 0
…………………….
Xét hàm số:
2 2
5
f(x) log 2 x x 2 1 x x 3 x
¡
Đặt
2
2
1 7 7
t x x 2 x t
2 4 2
Ta được
2
57
f(t) log 2t 1 t 5 t ;
2

'7
f (t) 0; t ; và f(2)=0
2

, Nên Hàm số f(t) đồng biến trong 7;
2

+
2 2
5
x 2 0 x 2
(I)
log 2 x x 2 1 x x 3 0
f(t) 0 f (2)
2
x 2
x 2
x 2
x 2
x 1
t 2 x x 2 2 x 2
(*) …………………
+
2 2
5
x 2 0 x 2
(II)
log 2 x x 2 1 x x 3 0
f(t) 0 f (2)
2
x 2
x 2 x 2
1 x 2
t 2 1 x 2
x x 2 2
(**) ……
Từ (*) và (**) Suy ra tập nghiệm của bpt đã cho là
S 1;

………….
0,25
0,25
0,25
0,25
Câu 4: (1,0 điểm)
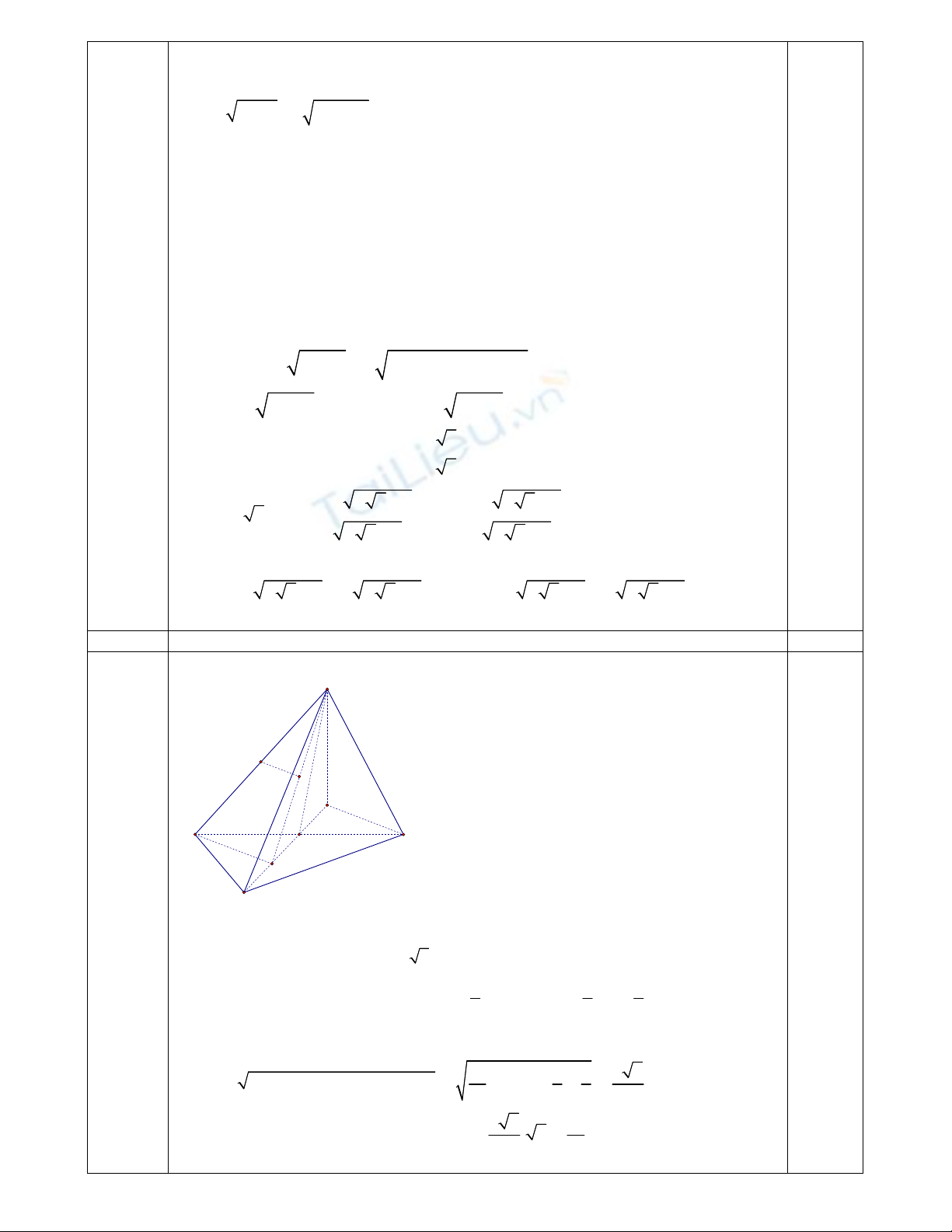
3 3 2
2 2 2
3 3 2 0 (1)
1 3 2 1 0 (2)
x y y x
x x y y
Điều kiện: 2
2
1 0 1 1
0 2
2 0
x x
y
y y
……………………………….
Đặt
t x 1 x t 1, t 0;2
ta có (1) 3 3 2 3 3 2
3 3 2 0 ( 1) 3 3( 1) 2 0
x y y x t y y t
t3 3t2 = y3 3y2 (*)
Hàm số f(u) = u3 3u2 nghịch biến trên đoạn [0; 2] nên:
3 2 3 2
(*) t 3t y 3y f(t) f (y) t y
y = x + 1 ... ..... ...
2 2 2
(2) 1 3 2( 1) ( 1) 1 0
x x x x
2 2
2 1 1 0
x x Đặt
2
1
v x
v[0; 1]
(2) 2v13
v 2v 2 0
v 1 3 (loai)
x 2 3 3 y 1 2 3 3
v 1 3
x 2 3 3 y 1 2 3 3
…………………….
Vậy hệ đã cho có hai nghiệm
(x;y) ( 2 3 3;1 2 3 3)và (x;y) ( 2 3 3;1 2 3 3)
…..
0,25
0,25
0,25
0,25
Câu 5: (1,0 điểm)
600
300
K
J
I
BC
A
H
S
*Tam giác ABC vuông tại A,
· ·
0 0
ACB 30 ABC 60 ,AC a 3;BC 2a
* I là trung điểm BC nên
1 1 a
IA IB IC BC a; IH IA
2 2 2
·
·
·
0
SH (ABC) (SC,(ABC)) (SC,HC) SCH 60
2
2 2 0 2
a a 1 a 3
HC IH IC 2IH.IC.cos60 a 2. .a.
4 2 2 2
Trong tam giác SHC: 0
a 3 3a
SH HC.tan60 . 3
2 2
......................
0,25
2
ABC
AB.AC a.a 3 a 3
S
2 2 2
2 3
S.ABC ABC
1 1 a 3 3a a 3
V .S .SH . .
3 3 2 2 4
(đvtt) .....................................
Gọi J là trung điểm AI, tam giác ABI đều nên
BJ AI
a 3
BJ (SAH) d(B,(SAH)) BJ
2
BJ SH
............................
K là trung điểm SB nên
1 1 a 3
d(K,(SAH)) .d(B,(SAH)) .BJ
2 2 4
..........
0,25
0,25
0,25
Câu 6: (1,0 điểm)
Ta có:
3
7 2a 3b 4c 1 (2a 1) (3b 2) (4c 3) 3. (2a 1)(3b 2)(4c 3)
3
1
0 (2a 1)(3b 2)(4c 3)
3
*
1 1 1
A 2a 3b 4c
2a 1 3b 2 4c 3
1 1 1
(2a 1) (3b 2) (4c 3) 6
2a 1 3b 2 4c 3
3
3
3
3. (2a 1)(3b 2)(4c 3) 6
(2a 1)(3b 2)(4c 3)
.......................
Đặt 3
1
t (2a 1)(3b 2)(4c 3); 0 t
3
3 1
A 3t 6; 0 t
t 3
Đặt 2
'2 2
3 3 3t 3 1
f(t) 3t 6 f (t) 3 0, t 0;
t 3
t t
....................
Suy ra hàm f(t) nghịch biến trên
1
0;
3
Do đó: 1 1
0 t f(t) f 16
3 3
Vậy
A f(t) 16
. Giá trị nhỏ nhất của biểu thức A là 16 .................................
Khi 3
1 2
2a 1 a
3 3
1
t (2a 1)(3b 2)(4c 3)
1 7
3b 2 b
3
3 9
2a 1 3b 2 4c 3
1 5
4c 3 c
3 6
................
0,25
0,25
0,25
0,25
Câu 7.a (1,0 điểm)
2x-y+1=0
H(1;-1) M(-1;2)
A
C
B
*Pt đường cao AH đi qua H(1;-1) và vuông góc với BC là:
AH : 1(x 1) 2(y 1) 0 x 2y 1 0
.........................................
0,25