Trang 1/6 - Mã đề 102
SỞ GD&ĐT NGHỆ AN
LIÊN TRƯỜNG THPT
KÌ THI THỬ TỐT NGHIỆP THPT NĂM 2024
Môn: Toán, Lớp 12
ĐỀ CHÍNH THỨC
(Đề thi có 06 trang)
Thời gian: 90 phút (Không kể thời gian phát đề)
Họ và tên:…………………………………………………..........SBD:……………......
Mã đề thi
102
Câu 1. Hàm số nào dưới đây đồng biến trên khoảng
0; ?
A. .B. .C. .D. .
1
3
logy x
0.5
logy x
3
logy x
Câu 2. Cho khối nón có chiều cao và bán kính đáy . Thể tích của khối nón bằng
6h
4r
A. .B. .C. .D. .
16
32
56
48
Câu 3. Cho số phức . Phần ảo của số phức bằng
3 2z i
z
A. .B. .C. D. .
2
2i
2
2i
Câu 4. Tập nghiệm của bất phương trình là
2
5 125
x
A. .B. .C. .D. .
3
;2

3;
2

3;3
2
3;
2

Câu 5. Tập nghiệm của bất phương trình là
5 5
log 5 log 5x
A. .B. .C. .D. .
1;
1;
;1
0;1
Câu 6. Cho cấp số cộng với và công sai . Giá trị của bằng
n
u
12u
3d
2
u
A. .B. .C. .D. .
1
3
2
5
6
Câu 7. Cho khối chóp có diện tích đáy và chiều cao . Thể tích của khối chóp đã cho bằng
2
5B a
3h a
A. .B. .C. .D. .
3
5a
2
5a
3
8a
3
15a
Câu 8. Đạo hàm của hàm số là
1
5x
y
A. .B. .C. .D. .
1
5x
y
1 5x
y x
1
5
ln 5
x
y
5.5 .ln 5
x
y
Câu 9. Cho hình nón có diện tích xung quanh bằng và có bán kính đáy . Độ dài đường sinh của
10
2r
l
hình nón đã cho bằng
A. .B. .C. .D. .
8l
5l
5
2
l
6l
Câu 10. Cho hàm số . Khẳng định nào dưới đây đúng?
32f x x x
A. .B. .
4 2
df x x x x C
2
d 3 2f x x x x C
C. .D. .
4 2
1
d4
f x x x x C
4 2
1 1
d4 2
f x x x x C
Câu 11. Cho khối hộp , biết khối chóp có thể tích thì khối hộp
.ABCD A B C D
.A A B C D
V
có thể tích bằng
.ABCD A B C D
A. .B. .C. .D. .
2V
3V
6V
3
V
Câu 12. Cho hàm số . Hàm số không thể nhận giá trị nào dưới đây:
1
3
f x x
A. .B. .C. .D. .
1
6
2
0, 25
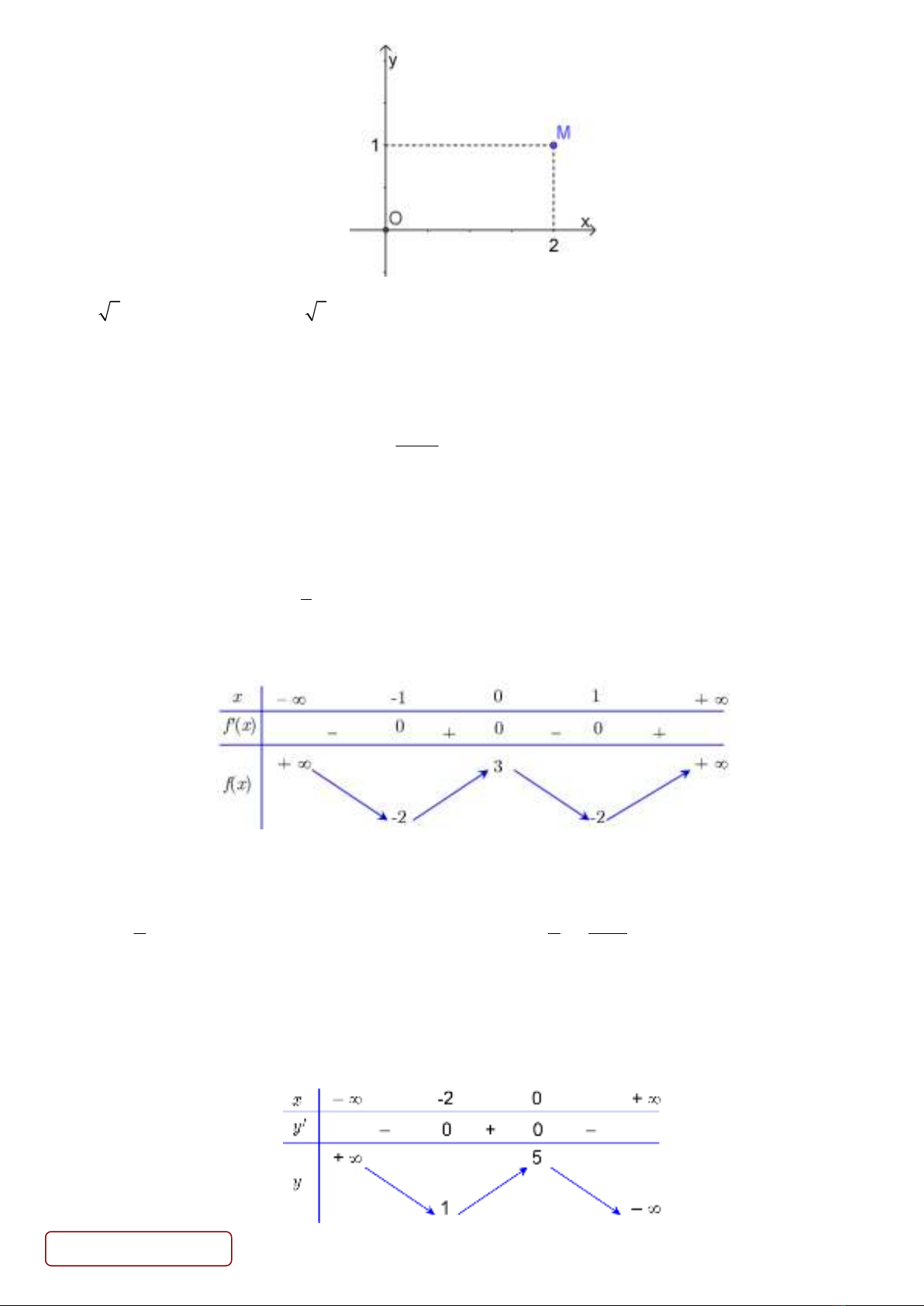
Câu 13. Điểm trong hình bên là điểm biểu diễn của số phức .
M
z
Trang 2/6 - Mã đề 102
Mô đun của là
z
A. .B. .C. .D. .
5
3
5
2
Câu 14. Lớp 12A có 30 học sinh. Có bao nhiêu cách chọn 3 học sinh tùy ý của lớp 12A để tham gia 1 trò chơi?
A. .B. .C. .D. .
24360
3
30
90
4060
Câu 15. Cho hai số phức và . Phần thực của số phức bằng
1 2
z z
A. .B. .C. .D. .
3
7
1
3
Câu 16. Tiệm cận đứng của đồ thị hàm số có phương trình là
A. .B. .C. .D. .
2y
2x
3x
3y
Câu 17. Trong không gian , cho mặt cầu . Bán kính của mặt cầu
Oxyz
2 2 2
: 2 1 3 9S x y z
S
là
A. .B. .C. .D. .
2R
9R
1R
3R
Câu 18. Nếu thì bằng
4
1
d 6f x x
4
1
11 d
3f x x
A. .B. .C. .D. .
7
9
5
3
Câu 19. Cho hàm số có bảng biến thiên như sau
y f x
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. .B. .C. .D. .
1;
0;1
; 1
;0
Câu 20. Với các số thực dương bất kì. Mệnh đề nào dưới đây đúng?
,a b
A. .B. .
log log log
ab a
b
log
log log
a a
b b
C. . D. .
log log .logab a b
log log logab a b
Câu 21. Trong không gian cho hai điểm và . Tọa độ của vectơ là
Oxyz ,
2; 1;3A
4;2; 5B
AB
A. .B. .C. .D. .
2; 3;8
2;3; 8
2;1;8
6;1; 2
Câu 22. Cho hàm số bậc ba có bảng biến thiên như hình vẽ.
y f x
Trang 3/6 - Mã đề 102
Số nghiệm thực của phương trình là
5 6 0f x
A. .B. .C. .D. .
0
2
3
1
Câu 23. Số giao điểm của đồ thị hàm số và đồ thị hàm số là
3 2
3y x x
2
3y x x
A. .B. .C. .D. .
0
3
1
2
Câu 24. Cho và thỏa mãn , giá trị của bằng
0b
0, 1a a
3
2021 2024
log .
aa b
A. .B. .C. .D. .
2023
3
2025
3
2027
3
1013
Câu 25. Cho hàm số liên tục trên và có bảng xét dấu của như sau:
y f x
f x
Số điểm cực trị của hàm số đã cho là
A. .B. .C. .D. .
4
1
2
3
Câu 26. Trong không gian phương trình đường thẳng đi qua điểm và vuông góc với mặt
Oxyz
d
2; 1; 1M
phẳng là
: 2 3 2 0P x y z
A. .B. .
2 3 1
1 2 3
x y z
2 1 1
1 2 3
x y z
C. .D. .
2 3 1
1 2 3
x y z
4 3 5
1 2 3
x y z
Câu 27. Cho hai số phức và . Môđun của số phức bằng
3z i
1w i
A. .B. .C. .D. .
2 5
3 5
4 5
6
Câu 28. Trong không gian mặt cầu có tâm và đi qua điểm có phương trình là
Oxyz ,
1;2; 3I
1;0; 2A
A. B.
2 2 2
1 2 3 3.x y z
2 2
2
1 2 9.x y z
C. D.
2 2 2
1 2 3 9.x y z
2 2 2
1 2 3 9.x y z
Câu 29. Trong không gian , cho mặt phẳng . Mặt phẳng có một vectơ pháp tuyến là
Oxyz
//P Oxz
P
A. .B. .C. .D. .
0;1;0n
1;0; 0n
1;0;1n
0;0;1n
Câu 30. Cho hàm số bậc ba có bảng biến thiên như hình vẽ
y f x
Khẳng định nào dưới đây đúng?
A. .B. .C. .D. .
2 3f f
72
2
f f
0 2f f
2 2f f
Câu 31. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
Trang 4/6 - Mã đề 102
A. .B. .C. .D. .
4 2
2 1y x x
33 1y x x
4 2
2 1y x x
33 1y x x
Câu 32. Trong không gian cho điểm ba điểm đường thẳng qua và
Oxyz
1;2; 1 , 4;3;2 , 1;2;3A B C
A
song song với có phương trình là
BC
A. .B. .C. .D. .
1 5
2
1
x t
y t
z t
1 5
2
1
x t
y t
z t
1 5
2
1
x t
y t
z t
1 5
2 2
1
x t
y t
z t
Câu 33. Cho hàm số có bảng biến thiên như sau
y f x
Điểm cực tiểu của hàm số đã cho là
A. B. C. D.
2.x
1.x
3.x
2.x
Câu 34. Nếu và thì bằng
2
0
d 2f x x
5
0
du 8f u
5
2
dtf t
A. .B. .C. .D. .
10
6
10
6
Câu 35. Cho hình chóp có đáy là hình vuông cạnh , , . Góc giữa mặt
.S ABCD
2a
SA ABCD
2SA a
phẳng và mặt phẳng bằng
SBC
SCD
A. .B. .C. .D. .
45
90
30
60
Câu 36. Trong một đề thi trắc nghiệm môn Toán có loại câu hỏi trả lời dạng đúng sai. Một câu hỏi có 4 ý hỏi,
mỗi ý hỏi học sinh chỉ cần trả lời đúng hoặc chỉ trả lời sai. Nếu 1 ý trả lời đúng đáp án thì được 0,1 điểm, đúng
đáp án 2 ý được 0,25 điểm, đúng đáp án 3 ý được 0,5 điểm và đúng đáp án cả 4 ý được 1 điểm. Giả sử một thí
sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại đúng sai này. Tính xác suất để
học sinh đó được 0,5 điểm ở phần trả lời 2 câu hỏi này.
A. .B. .C. .D. .
5
32
11
64
5
256
1
32
Câu 37. Cho hàm số . Khi đó bằng
3khi 1
2 1 khi 1
x x
y f x x x
3
1df x x
A. .B. .C. .D. .
2
4
0
6
Câu 38. Cho khối chóp đều có thể tích bằng và cạnh đáy bằng . Gọi là trung điểm của
.S ABC
3
3a
2a
M
cạnh , khoảng cách từ điểm đến mặt phẳng bằng
SA
M
ABC
A. .B. .C. .D. .
2 3a
3a
4 3a
3 3a
Câu 39. Cho hàm số bậc ba và hàm số bậc hai có đồ thị như hình vẽ.
y f x
y g x
Trang 5/6 - Mã đề 102
Biết rằng đồ thị hàm số cắt đồ thị hàm số tại ba điểm phân biệt có hoành độ
y f x
y g x
1 2 3
, ,x x x
thoả mãn . Diện tích miền tô đậm nằm trong khoảng nào sau đây?
1 2 3
2 9x x x
A. .B. .C. .D. .
13
6; 2
13 ;7
2
11
5; 2
11;6
2
Câu 40. Cho hàm số liên tục và có đạo hàm trên , thỏa mãn các điều kiện và
y f x
0;
1 1f
. Biết . Giá trị bằng
2
2 2 2
4 1 .e .e , 0;
x f x
x
x x f x x x
3 ln 3 ,f a b a b
3a b
A. .B. .C. .D. .
12
14
11
15
Câu 41. Trong không gian cho các điểm và hai đường thẳng lần lượt có
Oxyz
5;7;0 , 5;8; 4M Q
phương trình: . Biết điểm di động trên đường thẳng và điểm di động trên
1 2
1 5
: 3 ; : 3
3 2
x t x
y y
z z t
N
1
P
đường thẳng . Giá trị nhỏ nhất của là
2
T MN NP PQ
A. .B. .C. .D. .
369
459
179
289
Câu 42. Trong không gian cho mặt cầu có tâm thuộc đường thẳng và đi qua
,Oxyz
S
I
4
:5 7 2
x y z
hai điểm . Mặt cầu tiếp xúc với mặt phẳng nào dưới đây?
2; 1;2 , 2;3; 2M N
S
A. .B. .
: 2 2 5 0x y z
: 2 2 8 0P x y z
C. .D. .
: 2 2 1 0R x y z
: 2 2 9 0x y z
Câu 43. Có bao nhiêu số nguyên thoả mãn điều kiện sau:
1;2024x
?
2
3 3
0,4 5
3
log 6log 50
log log 0
log 4
x x
x
A. .B. .C. .D. .
1536
1537
1535
1538
Câu 44. Trên tập hợp số phức, xét phương trình (với là tham số). Biết phương trình đã cho
24 0,z mz
m
có hai nghiệm phân biệt . Các điểm biểu diễn các số phức tạo thành một đa giác lồi có
1 2
,z z
1 2
1 2
1 1
, , ,z z z z
diện tích lớn nhất bằng
A. .B. .C. .D. .
15
4
3
15
8
2
Câu 45. Có bao nhiêu cặp số thỏa mãn điều kiện sau:
;x y
?
4 2 2 2 2 2
2 2 5
5 7 . log 2 4 16 2 log 3log 5 3 1
x y y y x x x y y x x
A. .B. .C. .D. .
6
4
8
2