
S GD & ĐT H ng Yênở ư Đ THI TH Đ I H C NĂM 2010 L N 2Ề Ử Ạ Ọ Ầ
Tr ng THPT Tr n H ng Đ oườ ầ ư ạ Môn: Toán - Th i gian: 180 phútờ
Đ Bàiề
Câu I: (2 đi m) ểCho hàm s : ố
( )
3 2
3 1 9 2y x m x x m= − + + + −
(1) có đ th là (Cồ ị m)
1) Kh o sát và v đ th hàm s (1) v i m=1.ả ẽ ồ ị ố ớ
2) Xác đ nh m đ (Cị ể m) có c c đ i, c c ti u và hai đi m c c đ i c c ti u đ i x ngự ạ ự ể ể ự ạ ự ể ố ứ
v i nhau qua đ ng th ng ớ ườ ẳ
1
2
y x=
.
Câu II: (2,5 đi m)ể
1) Gi i ph ng trình: ả ươ
( )
( )
3
sin 2 cos 3 2 3 os 3 3 os2 8 3 cos sinx 3 3 0x x c x c x x+ − − + − − =
.
2) Gi i b t ph ng trình : ả ấ ươ
( )
2
2 1
2
1 1
log 4 5 log
2 7
x x x
+ − >
+
.
3) Tính di n tích hình ph ng gi i h n b i các đ ng: y = x.sin2x, y = 2x, x =ệ ẳ ớ ạ ở ườ
2
π
.
Câu III: (2 đi m) ể
1) Cho hình lăng tr ABC.A’B’C’ có đáy ABC là tam giác đ u c nh a, c nh bênụ ề ạ ạ
h p v i đáy m t góc là 45ợ ớ ộ 0. G i P là trung đi m BC, chân đ ng vuông góc h t A’ọ ể ườ ạ ừ
xu ng (ABC) là H sao cho ố
1
2
AP AH=
uuur uuur
. g i K là trung đi m AA’, ọ ể
( )
α
là m t ph ngặ ẳ
ch a HK và song song v i BC c t BB’ và CC’ t i M, N. Tính t s th tích ứ ớ ắ ạ ỉ ố ể
' ' '
ABCKMN
A B C KMN
V
V
.
2) Gi i h ph ng trình sau trong t p s ph c: ả ệ ươ ậ ố ứ
( )
2
2
2 2 2 2
65
6 0
a a a a
a b ab b a a
+ − =
+
+ + + − =
Câu IV: (2,5 đi m)ể
1) Cho m bông h ng tr ng và n bông h ng nhung khác nhau. Tính xác su t đ l yồ ắ ồ ấ ể ấ
đ c 5 bông h ng trong đó có ít nh t 3 bông h ng nhung? Bi t m, n là nghi m c aượ ồ ấ ồ ế ệ ủ
h sau:ệ
2 2 1
3
1
9 19
2 2
720
m
m n m
n
C C A
P
−+
−
+ + <
=
2 ) Cho Elip có ph ng trình chính t c ươ ắ
2 2
1
25 9
x y
+ =
(E), vi t ph ng trình đ ngế ươ ườ
th ng song song Oy và c t (E) t i hai đi m A, B sao cho AB=4.ẳ ắ ạ ể
3) Vi t ph ng trình m t ph ng cách đ u hai đ ng th ng dế ươ ặ ẳ ề ườ ẳ 1 và d2 bi t:ế
1
2
: 2
3
x t
d y t
z t
= +
= +
= −
2
1 2 1
:2 1 5
x y z
d
− − −
= =
Câu V: (1 đi m) ểCho a, b, c
0
≥
và
2 2 2
3abc+ + =
. Tìm giá tr nh nh t c a bi u th cị ỏ ấ ủ ể ứ
3 3 3
2 2 2
1 1 1
a b c
P
b c a
= + +
+ + +
……………………H t………………………ế
ĐÁP ÁN Đ THI TH Đ I H C L N 2Ề Ử Ạ Ọ Ầ
Bài
1
1
Khi m = 1 ta có hàm s : ố
3 2
6 9 1y x x x= − + −
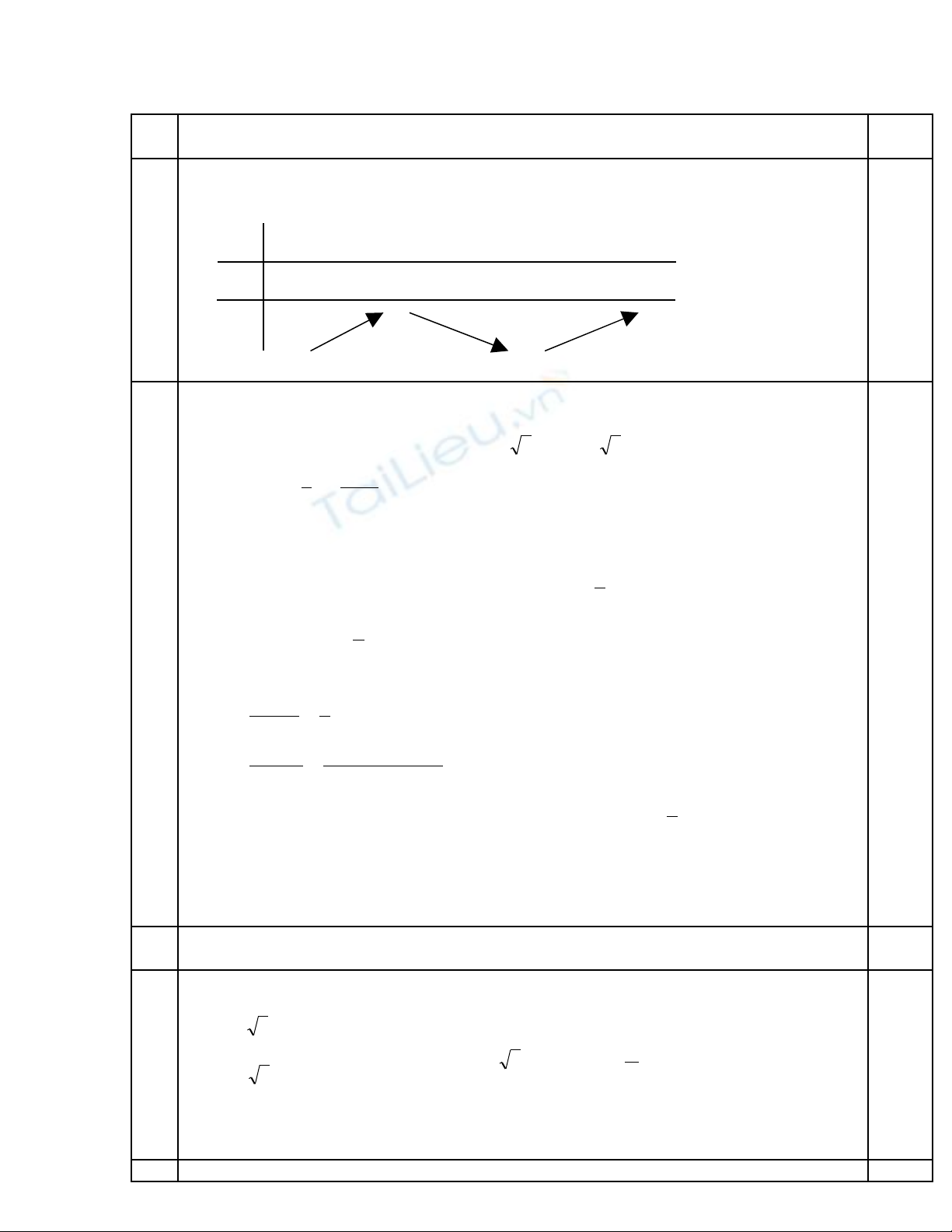
•BBT:
x -
∞
1 3 +
∞
y/ + 0 - 0 +
3 +
∞
y
-
∞
1
1đ
2
9)1(63' 2++−= xmxy
Đ hàm s có c c đ i, c c ti u:ể ố ự ậ ự ể
09.3)1(9' 2>−+=∆ m
);31()31;( +∞+−∪−−−∞∈⇔ m
Ta có
( )
14)22(29)1(63
3
1
3
122 ++−+−++−
+
−= mxmmxmx
m
xy
V y đ ng th ng đi qua hai đi m c c đ i và c c ti u làậ ườ ẳ ể ự ạ ự ể
14)22(2 2++−+−= mxmmy
Vì hai đi m c c đ i và c c ti u đ i x ng qua đt ể ự ạ ự ể ố ứ
xy 2
1
=
ta có đi u ki n c n làề ệ ầ
[ ]
1
2
1
.)22(2 2−=−+− mm
−=
=
⇔=−+⇔ 3
1
032
2
m
m
mm
Khi m = 1
⇒
ptđt đi qua hai đi m CĐ và CT là:y = - 2x + 5. T a đ trung đi m CĐ vàể ọ ộ ể
CT là:
=
++−
=
+
==
+
1
2
10)(2
2
2
2
4
2
2121
21
xxyy
xx
T a đ trung đi m CĐ và CT là (2; 1) thu c đ ng th ng ọ ộ ể ộ ườ ẳ
xy 2
1
=
1=⇒ m
tm .
Khi m = -3
⇒
ptđt đi qua hai đi m CĐ và CT là: y = -2x – 11.ể
3
−=⇒
m
không th a mãn. ỏ
V y m = 1 th a mãn đi u ki n đ bài.ậ ỏ ề ệ ề
1đ
Bài
2
1 ph ng trình đ a v :ươ ư ề
=
=
=
⇔
=−+
=−
⇔
=+−−−⇔
)(4cos
1cos
3tan
04cos3cos
0sincos3
0)8cos6cos2)(sincos3(
2
2
loaix
x
x
xx
xx
xxxx
Ζ∈
=
+=
⇔k
kx
kx ,
2
3
π
π
π
1 đ
2
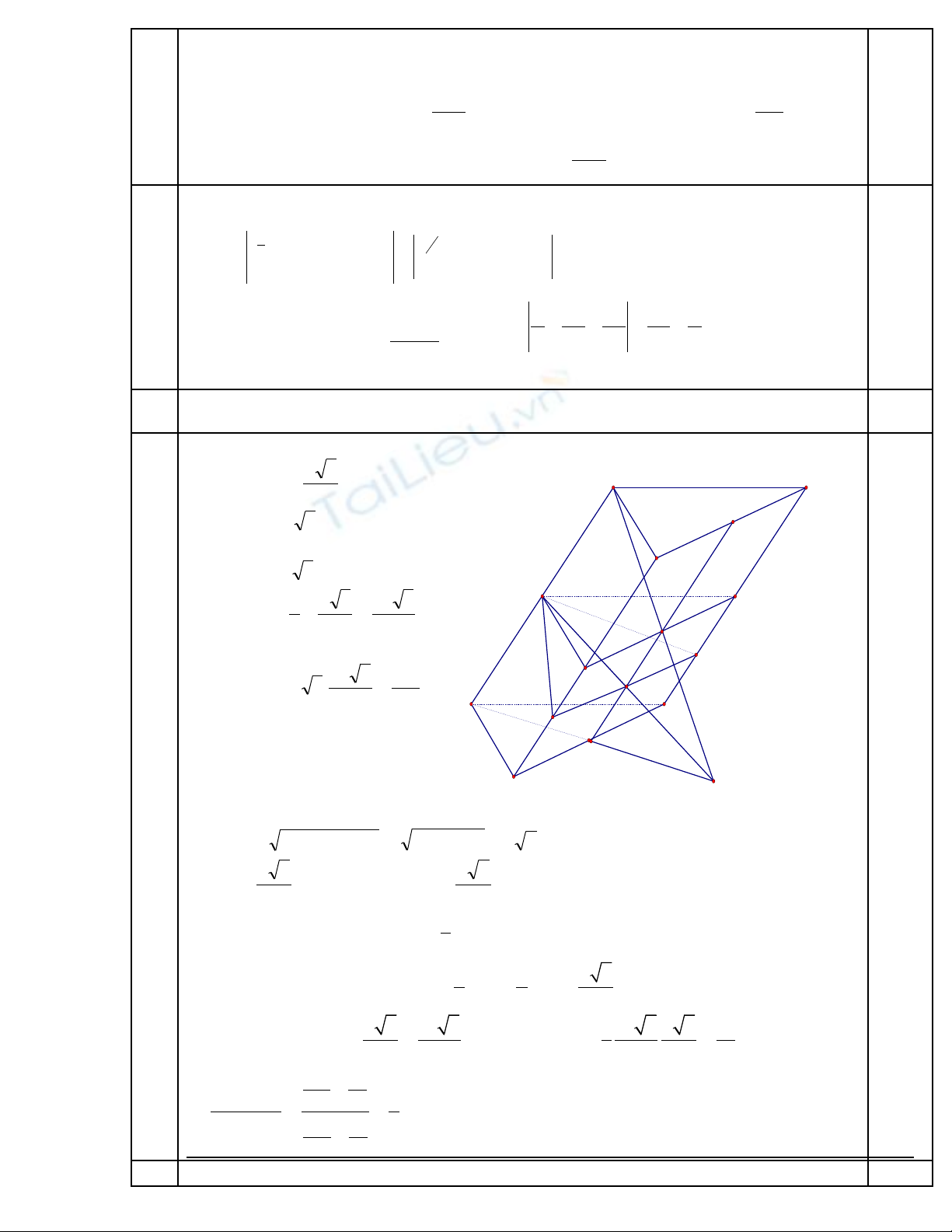
Đk:
−>
+∞∪−−∞∈
⇔
>+
>−+
7
);1()5;(
07
054
2
x
x
x
xx
)1()5;7( ∞+∪−−∈⇒ x
T pt ừ
7
1
log2)54(log
2
2
2
+
−>−+⇒
x
xx
2 2
2 2
27
log ( 4 5) log ( 7) 5
x x x x
−
⇔ + − > + ⇔ <
K t h p đi u ki n: V y BPT có nghi m: ế ợ ề ệ ậ ệ
)
5
27
;7( −
−∈x
0.75đ
3Ta có: x.sin2x = 2x
⇔
x.sin2x – 2x = 0
⇔
x(sin2x – 2) =0
⇔
x = 0
Di n tích hình ph ng là:ệ ẳ
∫∫ −=−= 2
0
2
0)22(sin)22sin.(
π
π
dxxxdxxxxS
Đ t ặ
−
−
=
=
⇒
−=
=
x
x
v
dxdu
dxxdv
xu
2
2
2cos
)22(sin
44424
222
πππππ
−=+−=⇔ S
(đvdt)
0.75đ
Bài
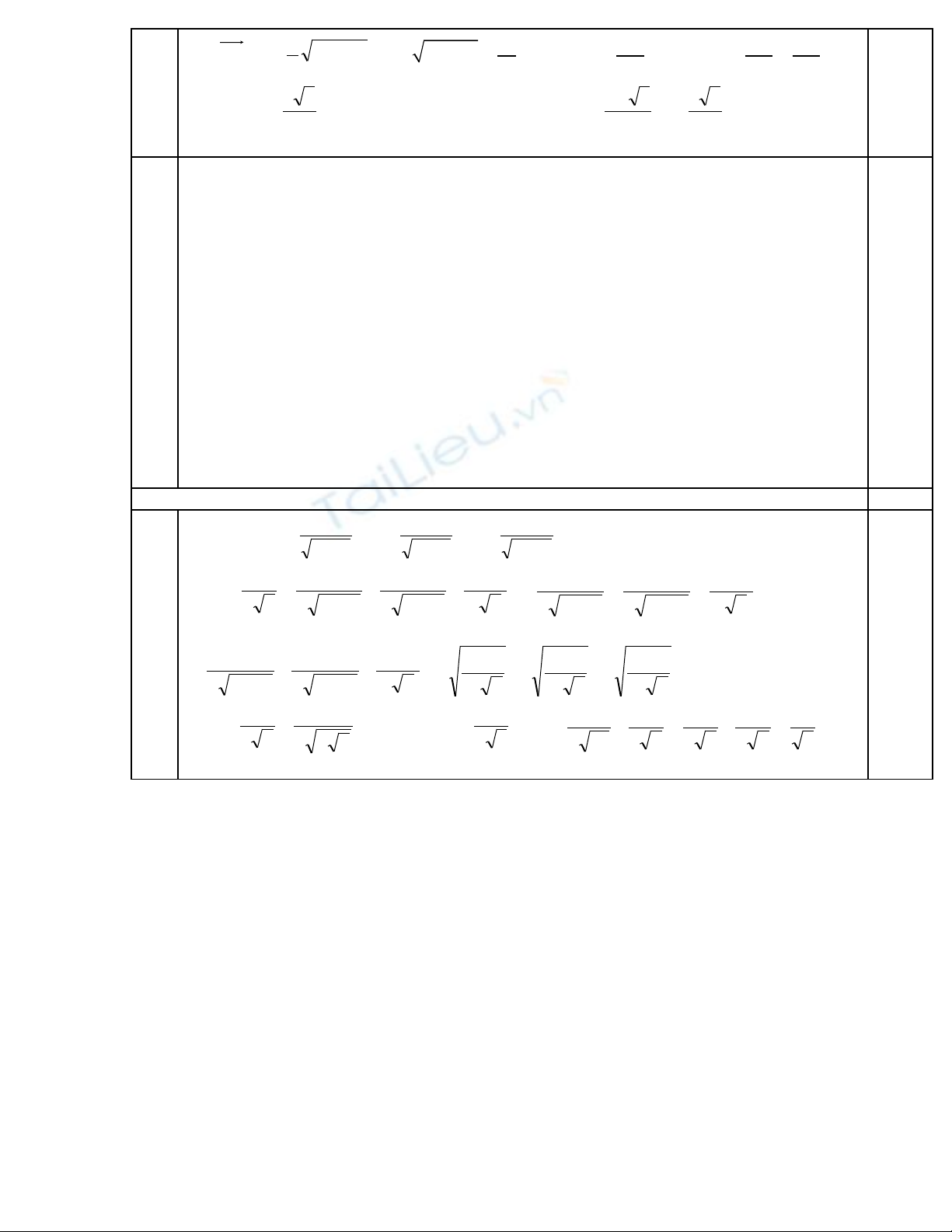
3
1G i Q, I, J l n l t là trung đi m B’C’, BB’, CC’ọ ầ ượ ể
ta có:
2
3a
AP =
3aAH =⇒
Vì
'' AHA∆
vuông cân t i H.ạ
V y ậ
3' aHA =
Ta có
4
3
2
3
.
2
12
aa
aS ABC ==
(đvdt)
4
3
4
3
.3
32
'''
aa
aV CBABCA ==⇒
(đ vt
t) (1)
Vì
'' AHA∆
vuông cân
( )
CCBBHKAAHK ''' ⊥⇒⊥⇒
G i E = MNọ
∩
KH
⇒
BM = PE =
CN (2)
mà AA’ =
22
'AHHA +
=
633 22 aaa =+
4
6
2
6a
CNPEBM
a
AK ===⇒=⇒
Ta có th tích K.MNJI là:ể
1.
3
1 1 6
'
2 4 4
MNJI
V S KE
a
KE KH AA
=
= = =
2
6 6
. . ( )
4 4
MNJI
a a
S MN MI a dvdt= = =
2 3
1 6 6 ( )
3 4 4 8
KMNJI
a a a
V dvtt⇒ = =
3 3
2 3
' ' '
3
1
8 8
32
8 8
ABCKMN
A B C KMN
a a
V
a a
V
−
⇒ = =
+
1đ
2ĐK:
0
2≠+ aa
45
E
K
J
I
A
B
C
C'
B'
A'
P
H
Q
N
M

T (1) ừ
06)(5)( 222 =−+−+⇔ aaaa
=+
−=+
⇔6
1
2
2
aa
aa
Khi
1
2−=+ aa
thay vào (2)
2
1 23.
2
6 0
1 23.
2
i
b
b b
i
b
− −
=
⇒ − − − = ⇔ − +
=
;
+−
=
−−
=
⇔=++
2
31
2
31
01
2
i
a
i
a
aa
Khi
6
2
=+ aa
=
−=
⇔2
3
a
a
Thay vào (2)
2
1 5
2
6 6 6 0
1 5
2
b
b b
b
− +
=
⇒ + − = ⇔ − −
=
V y h pt có nghi m (a, b) là:ậ ệ ệ
+−−−
−−−−
2
31
;
2
231
,
2
31
;
2
231 iiii
−−+−
−−+−
2
31
;
2
231
,
2
31
;
2
231 iiii
;
−−
+−
−−
−
+−
−
2
51
;2,
2
51
;2,
2
51
;3,
2
51
;3
Bài
41)
=
<++
−
+
−
720
2
19
2
9
1
12
3
2
n
mn
m
m
P
AcC
T (2): ừ
761!6720)!1( =⇔=−⇔==− nnn
Thay n = 7 vào
(1)
09920
19990
2
19
2
9
45
2
)1(
2
2
<+−⇔
<++−⇔
<++
−
⇔
mm
mmm
m
mm
119
<<⇔
m
vì
10
=⇒Ζ∈
mm
V y m = 10, n = 7. V y ta có 10 bông h ng tr ng và 7 bông h ng nhung, đ l yậ ậ ồ ắ ồ ể ấ
đ c ít nh t 3 bông h ng nhung trong 5 bông h ng ta có các TH sau:ượ ấ ồ ồ
TH1: 3 bông h ng nhung, 2 bông h ng tr ng có:ồ ồ ắ
1575. 2
10
3
7=CC
cách
TH2: 4 bông h ng nhung, 1 bông h ng tr ng có:ồ ồ ắ
350. 1
10
4
7=CC
cách
TH3: 5 bông h ng nhung có:ồ
21
5
7=C
cách
⇒
có 1575 + 350 + 21 = 1946 cách.
S cách l y 4 bông h ng th ng ố ấ ồ ườ
%45,31
6188
1946
6188
5
17
≈=⇒
=
P
C
2) G i ptđt // Oy là: x = a (d) tung đ giao đi m (d) và Elip là: ọ ộ ể
25
25
25
1
9
1
925
222
22
aay
ya
−
=−=⇔
=+
2
2
225
5
3
25
25
.9 ay
a
y−±=⇒
−
=⇒
V y ậ
−−
−22 25
5
3
;,25
5
3
;aaBaaA
−= 2
25
5
6
;0 aAB
;
2 2 2
10 100 100 125
25 25 25
3 9 9 9
a a a⇔ − = ⇔ − = ⇔ = − =
3
55
±=⇒ a
V y ph ng trình đ ng th ng: ậ ươ ườ ẳ
3
55
,
3
55 =
−
=xx
3)đ ng th ng dườ ẳ 2 có PTTS là:
+=
+=
+=
'51
'2
'21
tz
ty
tx
⇒
vect CP c a dơ ủ 1 và d2 là:
1 2
(1;1; 1), (2;1;5)
d d
u u= − =
r
⇒
VTPT c a mp(ủ
α
) là
1 2
. (6; 7; 1)
d d
n u u
α
= = − −
r r r
⇒
pt mp(
α
) có d ng 6x – 7y – z + D = 0ạ
Đ ng th ng dườ ẳ 1 và d2 l n l t đi qua 2đ’ M(2; 2; 3) và N(1; 2; 1)ầ ượ
( ,( )) ( ,( ))
|12 14 3 | | 6 14 1 |
| 5 | | 9 | 7
d M d N
D D
D D D
α α
⇒ =
− − + = − − +
⇔ − + = − + ⇔ =
V y PT mp(ậ
α
) là: 3x – y – 4z +
7 0=
Bài 5
Ta có: P + 3 =
2
2
3
2
2
3
2
2
3
111
a
a
c
c
c
b
b
b
a
+
+
++
+
++
+
24
1
1212
24
62
2
2
2
3b
b
a
b
a
P+
+
+
+
+
=+⇔
24
1
1212
2
2
2
2
3c
c
b
c
b+
+
+
+
+
+
24
1
1212
2
2
2
2
3a
a
c
a
c+
+
+
+
+
+
3
6
3
6
3
6
216
3
216
3
216
3cba ++≥
6
222
382
9
)(
222
3
22
3=++≥+⇒ cbaP
2
3
22
3
22
9
22
3
22
9
6 3 =−=−≥⇒ P
Đ PểMin khi a = b = c = 1






















![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



