Điều khiển hệ cầu trục dựa trên luật
PID
Tóm tắt:
Bài báo đưa ra mô hình toán của hệ cầu trục và các kết quả nghiên cứu thiết
kế bộ điều khiển cho chúng dựa trên luật PID với mong muốn giảm dao
động của tải và khả năng
ứng dụng vào thực tiễn.
Đặtvấnđề
Cầu trục là thiết bị công
nghiệp được ứng dụng rất
rộng rãi trong nhiều lĩnh
vực như trong xây dựng,
trong nhà máy hay tại
cảng bốc dỡ hàng ...
Những cầu trục này
thường vận hành bằng
tay. Khi mà kích thước
của cầu trục trở nên lớn
hơn và yêu cầu vận chuyển nhanh hơn thì quá trình điều khiển chúng sẽ
trở nên khó khăn nếu không tự động hoá quá trình này. Cầu trục dịch
chuyển theo quỹ đạo không cứng nhắc. Nhưng nó hoạt động dưới những
điều kiện hết sức khắc nhiệt và một hệ thống điều khiển kín là thích hợp
nhất.
Cầu trục là hệ phí tuyến lớn. Hơn nữa trong quá trình di chuyển phải đảm
bảo dao động của tải là nhỏ nhất. Vì thế khi thiết kế bộ điều khiển cho hệ
cầu trục phải tính đến các yếu tố này
Trong nhiều trường hợp vận hành không đòi hỏi cao về chất lượng thì
luật PID hoàn toàn đáp ứng được yêu cầu đặt ra. Việc cài đặt luật PID
không chỉ đơn giản mà chi phí lại khá thấp, dễ dàng trong sử dụng.
2. Luật điều khiển PID
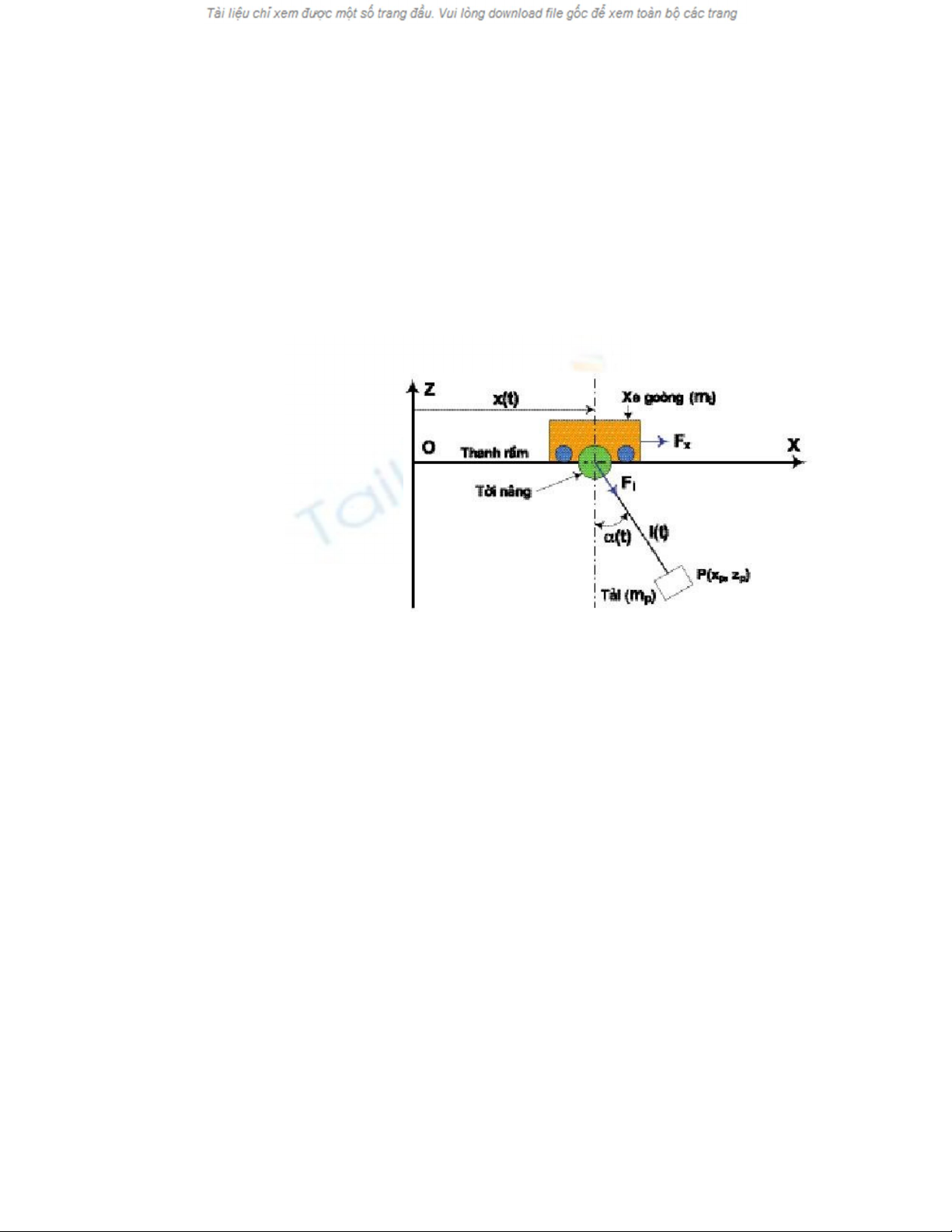
Hình 1: Mô hình chuyển động cầu trục trong
hệ toạ độ 2D

Bộ điều khiển PID được tạo nên từ ba thành phần: P-Propotion, I-
Integral, D-Derivation và được mô tả trên miền thời gian như sau:
trong đó: e(t) là tín hiệu đầu vào (sai lệch điều khiển), u(t) là tín hiệu đầu ra
(tín hiệu điều khiển), kP là hệ số khuếch đại, TI là hằng số thời gian tích
phân, TD là hằng số thời gian vi phân.
Hàm truyền đạt của bộ điều khiển PID như sau:
Các tham số kp, TI, TD hay kP, kI, kD cần phải xác định và hiệu chỉnh với
từng hệ thống để hệ kín đạt chất lượng mong muốn.
- Nếu sai lệch e(t) càng lớn thì thông qua thành phần P - tỉ lệ uP(t) , tín hiệu
điều chỉnh u(t) càng lớn.
- Nếu sai lệch e(t) vẫn khác 0, thì thông qua thành phần I - tích phân uI(t) ,
bộ điều khiển vẫn tạo tín hiệu điều chỉnh.
- Nếu tốc độ biến đổi của e(t) càng lớn thì thông qua thành phần D - vi phân
uD(t) , bộ điều khiển đưa tín hiệu điều chỉnh càng lớn.
Trong khi thiết kế bộ điều khiển cho đối tượng xác định không phải lúc nào
ta cũng bắt buộc phải xác định cả ba tham số kp, kI, kD. Khi mà trong đối
tượng có thành phần tích phân thì bộ điều khiển chỉ cần luật PD là đủ, còn
khi đối tượng thay đổi chậm và bản thân bộ điều khiển không cần phản ứng

thật nhanh với sai lệch thì sử dụng luật PI. Đơn giản nhất là bộ điều khiển
với chỉ luật P để đầu ra bám theo đầu vào.
Có rất nhiều phương pháp tính toán và chỉnh định tham số bộ điều khiển
PID có thể kể ra ở đây là phương pháp thứ nhất, thứ hai của Ziegler-Nichols,
tính toán theo nguyên lý tối ưu đối xứng, tính theo nguyên lý tối ưu độ lớn,
ngoài ra còn phải kể đến phương pháp của Chien – Hrones – Reswick [1].
3. Thiết kế bộ điều khiển phản hồi đầu ra cho hệ cầu trục
3.1 Mô hình toán hệ cầu trục
Để xây dựng mô hình toán của hệ cầu trục ta cần phải định nghĩa rõ ràng các
biến cho hệ. Mô hình cầu trục với hệ toạ độ được chọn như mô tả trên hình
1. Trục Ox nằm ngang dọc theo thanh rầm, trục Oz thẳng đứng có chiều
hướng lên trên. Xe goòng di chuyển trên thanh rầm với vị trí được xác định
bởi x(t) là khoảng cách đo được từ gốc O đến điểm treo của cáp nâng tải trên
xe. Coi tải như một chất điểm có khối lượng mP, xe goòng có khối lượng
mt. Tải trọng và xe goòng được nối với nhau bằng một cáp cứng có khối
lượng không đáng kể và có chiều dài l(t), sự dài ra của dây cáp là không
đánh kể. Trong khi nâng hạ tải hay di chuyển xe thì tải dao động trong mặt
phẳng thẳng đứng với góc lệch (t). Fx là lực chuyển động xe goòng theo
hướng x và Fl là lực nâng tải theo hướng l.
Phương trình chuyển động của hệ cầu trục thu được từ phương trình
Lagrange về cân bằng năng lượng của hệ.
Sau khi tính toán và biến đổi phương trình động lực học mô tả hệ thống như
sau [2]:
Để thao tác dễ hơn với các thông số hệ cầu trục, ta sẽ viết lại

phương trình chuyển động của hệ trong không gian trạng thái. Các phương
trình dưới đây sẽ được dùng để mô phỏng động học hệ thống. Chúng ta đặt
các biến trạng thái như sau:
Khi đó, từ phương trình động lực học ban đầu, ta có: Từ các phương trình
trên ta xây dựng được các khối mô hình ứng với
từng chuyển động tương ứng: chuyển động thẳng của xe, chuyển động nâng
tải, và dao động của tải. Sau cùng, kết hợp các chuyển động lại ta có mô
hình động lực học mô tả hệ cầu trục trên Matlab/Simulink
3.2 Thiết kế bộ điều khiển PID cho hệ cầu trục
Hình 2: Sơ đồ khối mô tả các th
ành
phần hệ cầu trục: DynamicX-
chuy
ển động thẳng của xe;
DynamicL-nâng tải; Dynamic_Anfa-
dao động tải
Hình 3: Mô hình đ
ộng lực học hệ
cầu trục trên Matlab
Giả thiết động học các khâu trong hệ độc lập với nhau, từ đó thành lập
phương trình chuyển động của từng thành phần trong hệ. Trên cơ sở đó lựa
chọn bộ điều khiển PID phù hợp cho từng nhánh chuyển động.
Phương trình chuyển động của xe goòng theo trục x, như sau

; với b là hệ số ma sát nhớt
Lựa chọn một luật điều khiển đơn giản hiệu quả (dựa trên luật PID) cho
thành phần vị trí xe goòng [1], [2], [4] được đưa ra là khâu PI có dạng:
trong đó xd là vị trí yêu cầu, kxp phệ số khâu P, kxi hệ số khâu I
Phương trình nâng tải theo phương l thẳng đứng khi bỏ qua ma sát, như sau
Theo [1], [2], [5] để giữ ổn định tải trong không gian ở một độ cao mong
muốn thì bộ điều khiển lựa chọn là luật PD có dạng
trong đó: ld là độ cao nâng tải mong muốn, kip hệ số khâu P, kiD hệ số
khâu D
Tuy nhiên, với thành phần nâng tải, bằng thực nghiệm và theo [3], [5] để đầu
ra bám theo đầu vào thì luật điều khiển PID sẽ mang lại chất lượng tốt hơn.
Thông số cầu trục được cho như sau:
* Khối lượng xe goòng: mt = 2[kg]
* Hệ số ma sát của xe: b = 20[N]
* Khối lượng tải: mp = 0.2[kg]
* Chiều dài cáp nâng tải thay đổi: 0.25-1[m]
* Khoảng cách di chuyển xe thay đổi: 0-1[m]
* Góc lắc dao động cho phép: = 10O ~ 0.2 rad


























