18 August 2009 Assoc. Prof. Hon.-Prof. Dr.-Ing. habil. Ng. Ph. Quang
Electrical Engineering - Automatic Control
1
Điềukhiểnsố
(Digital Control Systems)
PhầnA:
Môn họctruyềnđạtcáckiếnthứcphụcvụphân
tích, thiếtkếcác hệthống điềukhiểntựđộng sử
dụng vi xửlý (μP, μC, DSP).
PhầnA baogồmcácnội dung thuộcchương
trìnhdànhchoĐạihọc.
(Version 5, 8/2009)
18 August 2009 Assoc. Prof. Hon.-Prof. Dr.-Ing. habil. Ng. Ph. Quang
Electrical Engineering - Automatic Control
2
Điềukhiểnsố
Chương 1: Mô hình tín hiệuvàhệthống
1. Cấutrúccơsởcủahệthống ĐK số
2. Mô hình tín hiệutrênmiềnảnh z
3. Mô hình hệthống trên miềnảnh z
Chương 2: Điềukhiểncóphảnhồiđầura
1. Xét ổnđịnh củahệthống số
2. Thiếtkếtrên miềnthờigianxấpxỉliên tục
3. Thiếtkếtrên miềnthời gian gián đoạn
4. Mộtsốdạng mởrộng
18 August 2009 Assoc. Prof. Hon.-Prof. Dr.-Ing. habil. Ng. Ph. Quang
Electrical Engineering - Automatic Control
3
Điềukhiểnsố
Chương 3: Điềukhiểncóphảnhồitrạng thái
1. Ôn lạicáckiếnthứccơsở
2. Mô hình trạng thái gián đoạn
3. Tính ĐK được, QS đượcvàcácdạng chuẩn
4. Cấutrúccơbảncủahệthống ĐK sốtrên không
gian trạng thái
5. Mộtsốdạng mởrộng
Chương 4: Thực hiện kỹthuậthệthống ĐK số
1. Ảnh hưởng củasốhóa (lượng tửhóa) biên độ
2. Thiếtkếhệthống bằng máy tính (MATLAB)
3. Thiếtkếhệthống vi điềukhiển
18 August 2009 Assoc. Prof. Hon.-Prof. Dr.-Ing. habil. Ng. Ph. Quang
Electrical Engineering - Automatic Control
4
Điềukhiểnsố
Tài liệuthamkhảo:
[1] Isermann R.: Digitale Regelsysteme. Bd. I und II, Springer-Verlag, 2.
Auflage, 1987-1988
[2] Franklin G.F., Powell J.D., Workman M.L.: Digital Control of Dynamic
Systems. Addison Wesley, 2nd 1994
[3] Quang Ng.Ph.: MATLAB & Simulink dành cho kỹsưđiềukhiểntựđộng.
Nhà xuấtbản KH&KT, 2004
[4] Quang Ng.Ph., Dittrich A.-J.: Vector Control of Three-Phase AC
Machines. Springer, Berlin – Heidelberg, 2008
Chú ý: Giáo trình này sửdụng để dậycáclớpđạihọcvớithời
lượng 45 tiết, bao gồm lý thuyếtvàvídụ. Vớicáclớp 60
tiết, sẽdậygiống nhưlớp 45 tiếtnhưng có thêm bài tậplớn
12-15 tiết.
18 August 2009 Assoc. Prof. Hon.-Prof. Dr.-Ing. habil. Ng. Ph. Quang
Electrical Engineering - Automatic Control
5
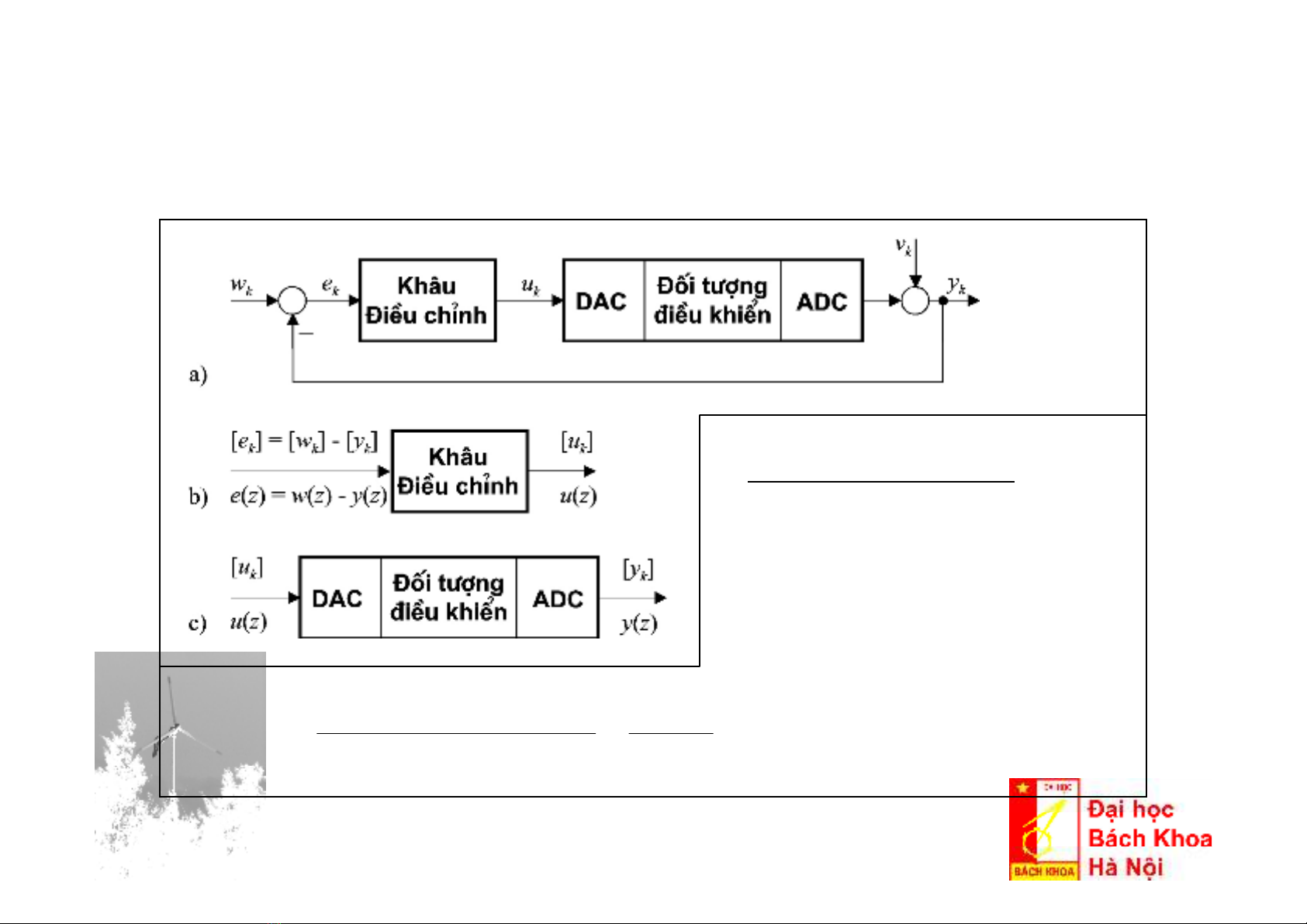
1. Mô hình tín hiệuvàhệthống
1.1 Cấutrúccơsởcủahệthống ĐK số
11 0
011
kkk
kk k
pu pu pu
qe qe qe
μμ
νν
−−
−−
++ + =
+++
()
(
)
(
)
1
1
01
ÐC 11
01
Qz
qqz qz
Gz ppz pz
P
z
ν
ν
μ
μ
−
−−
−−
−
+++
==
+++
Khâu Điềuchỉnh:
1. Pt. Sai phân
2. Hàm truyềnđạttrên
miềnảnh z