http://www.ebook.edu.vn
CHƯƠNG 6
TÍNH TOÁN ỨNG LỰC (ỨNG SUẤT) TRONG THÁP CỦA
CẦN TRỤC THÁP THEO QUAN ĐIỂM ĐỘNG LỰC HỌC
Đặt vấn đề
Cần trục tháp có tháp cao, độ mảnh lớn, kết cấu của cột (tháp) dạng dàn
không gian. Khi các bộmáy của cần trục làm việc độc lập hoặc đồng thời thì tải
trọng tác dụng tại một mặt phẳng tính toán nào đó tổng quát gồm các thành phần
ứng lực: Fx, Fy, Fz, Mx, My, Mz.
Các ứng lực này theo quan điểm động lực học, do trọng lượng của các bộ
phận, trọng lượng của hàng và lực căng trong cáp hàng, cáp cần gây ra.Bản thân
các lực căng cáp cũng là các hàm thay đổi theo thời gian. Chính vì vậy các ứng
lực này cũng là các hàm thay đổi theo thời gian và chúng gây ra các ứng suất
trong các thanh đứng và thanh xiên là các ứng suất động (hàm của thời gian).
Việc xác định các ứng lực (ứng suất này) là các hàm thời gian có một ý
nghĩa rất quan trọng trong việc tính toán mỏi, tuổi thọcủa kết cấu thép cần trục
tháp.
Để xác định được ứng lực này theo quan điểm động lực học, cần phải giải
bài toán động lực học, xác định được các toạ độ suy rộng để tính ra được các lực
căng cáp và từ đó tính được các ứng suất động.
Chúng ta chọn cần trục tháp kiểu tháp quay (KB 160-2 do Liên Xô cũ chế
tạo) làm đối tượng nghiên cứu.
Mô hình thực thểhiện ởHình 6-1, sơ đồ mắc cáp ởHình 6-2, mô hình động
lực học ởHình 6-3
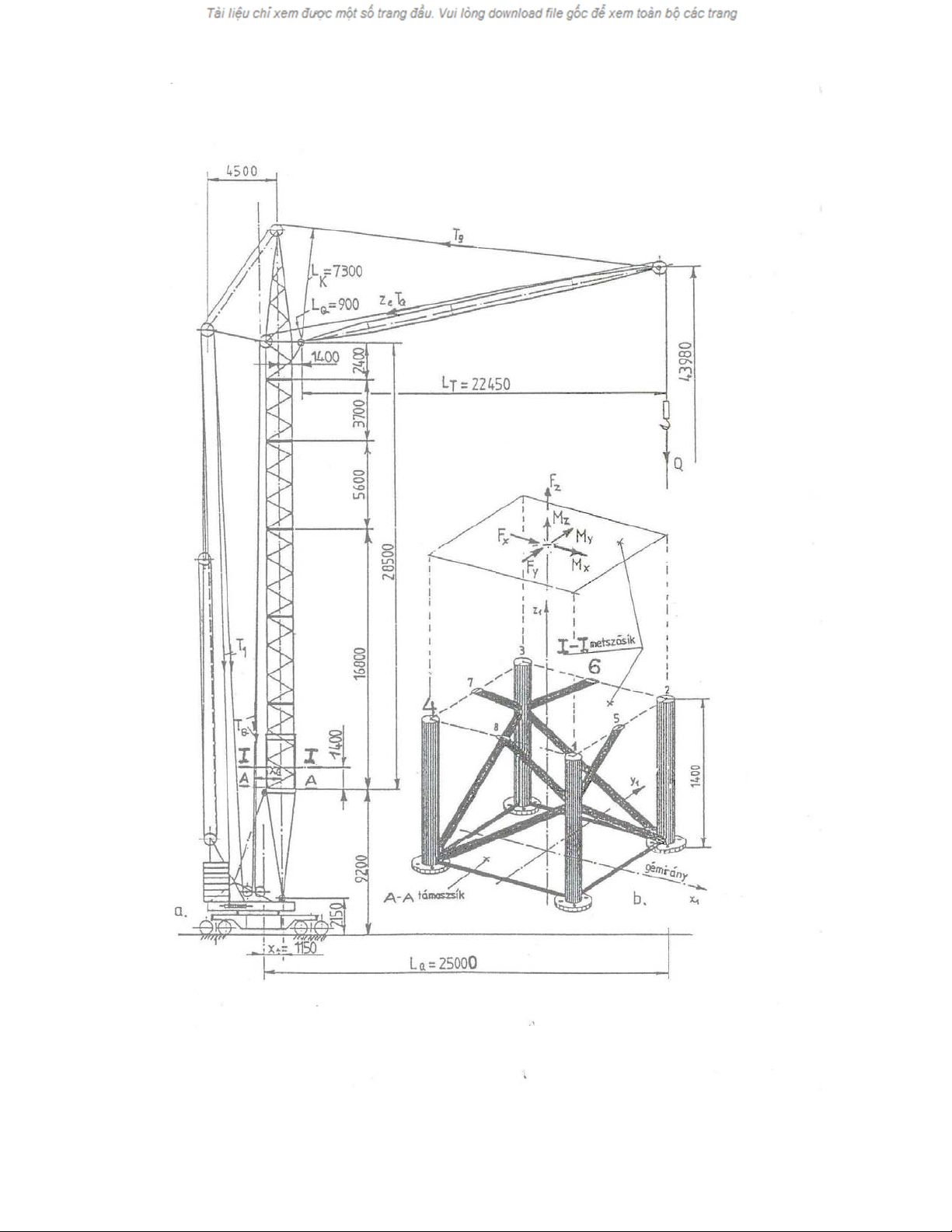
http://www.ebook.edu.vn
Hình 6-1. Tổng thể cần trục tháp kiểu tháp quay (KB–160-2)
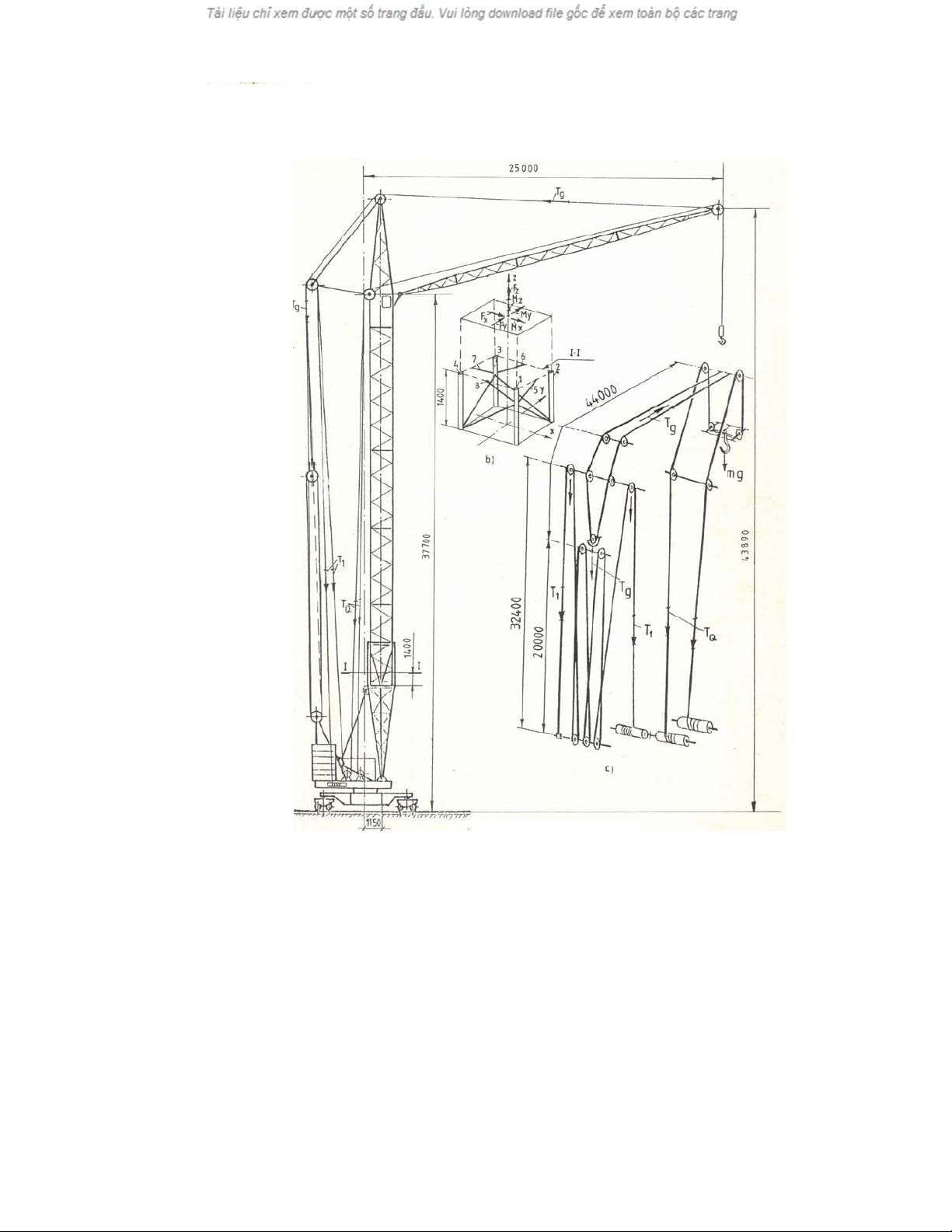
http://www.ebook.edu.vn
Hình 6-2. Sơ đồ mắc cáp của cần trục tháp
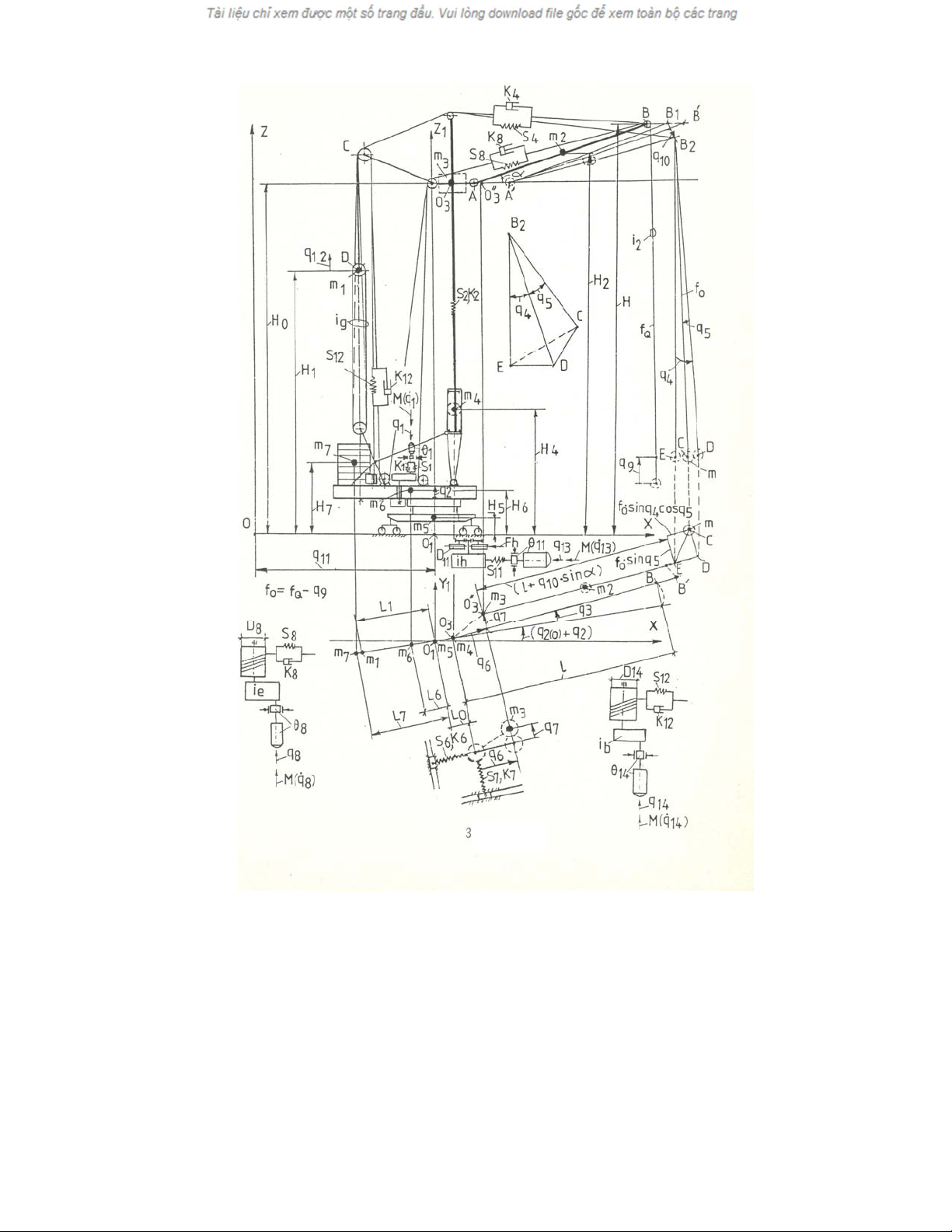
http://www.ebook.edu.vn
Hình 6-3. Mô hình động lực học
http://www.ebook.edu.vn
Trong đó:
q1, q8, q13, q14 -Tương ứng là góc quay trên trục động cơ của bộmáy quay,
bộmáy nâng, bộmáy di chuyển và bộmáy nâng hạcần
q2-Độ dịch chuyển góc của toa quay quanh trục quay của cần trục
q3-Độ dịch chuyển tương đối của tháp quanh trục riêng của nó (góc xoắn
khi biến dạng)
q4, q5-Độ dịch chuyển góc nghiêng của cáp hàng quanh đỉnh cần trong mặt
phẳng tháp - cần và trong mặt phẳng vuông góc với mặt phẳng trên.
q6, q7-Độ dịch chuyển của đỉnh tháp (chỗnối cần) trong mặt phẳng tháp -
cần và trong mặt phẳng vuông góc với mặt phẳng trên (biến dạng do uốn của
tháp trong 2 mặt phẳng chính của nó)
q9-Độ dịch chuyển của cáp hàng theo phương của cáp nâng hàng
q10 -Độ dịch chuyển của đỉnh cần (do góc quay tương đối của cần quanh
khớp bản lềnối với tháp)
q11 -Độ dịch chuyển của cần trục khi bộmáy di chuyển hoạt động
q12 -Độ dịch chuyển của puli động của bộmáy nâng hạcần
m1- Khối lượng cụm puli động
m2- Khối lượng của cần
m3- Khối lượng của tháp quy dẫn lên đỉnh tháp
m4- Khối lượng quy dẫn của phần cổng ởchân tháp
m5- Khối lượng của phần satxi
m6- Khối kượng của sàn toa quay
m7 - Khối lượng của đối trọng
S4, K4-Độ cứng và hệsốdập tắt dao động của cáp treo cần
S8, K8-Độ cứng và hệsốdập tắt dao động của cáp hàng
S1, K1-Độ cứng và hệsốdập tắt dao động của bộmáy quay
S12, K12 -Độ cứng và hệsốdập tắt dao động của cáp thuộc tời nâng hạcần
S11 -Độ cứng của bộmáy di chuyển
S6, S7, K6, K7-Độ cứng và hệsốdập tắt dao động quy dẫn của tháp theo 2
phương chính
S2, K2-Độ cứng và hệsốdập tắt dao động xoắn của tháp
)q(M),q(M),q(M),q(M 141381 tương ứng là các đường đặc tính cơ của bộ
máy quay, bộmáy nâng hạhàng, bộmáy di chuyển và bộmáy nâng hạcần (thay
đổi tầm với)
f0- Chiều dài ban đầu của cáp hàng
1
- Mômen quán tính của bộmáy quay
11
- Mômen quán tính của bộmáy di chuyển