http://www.ebook.edu.vn
CHƯƠNG 9
ĐỘNG LỰC HỌC CỦA MÁY SẢN XUẤT VẬT LIỆU XÂY DỰNG
9.1. Động lực học của máy sàng
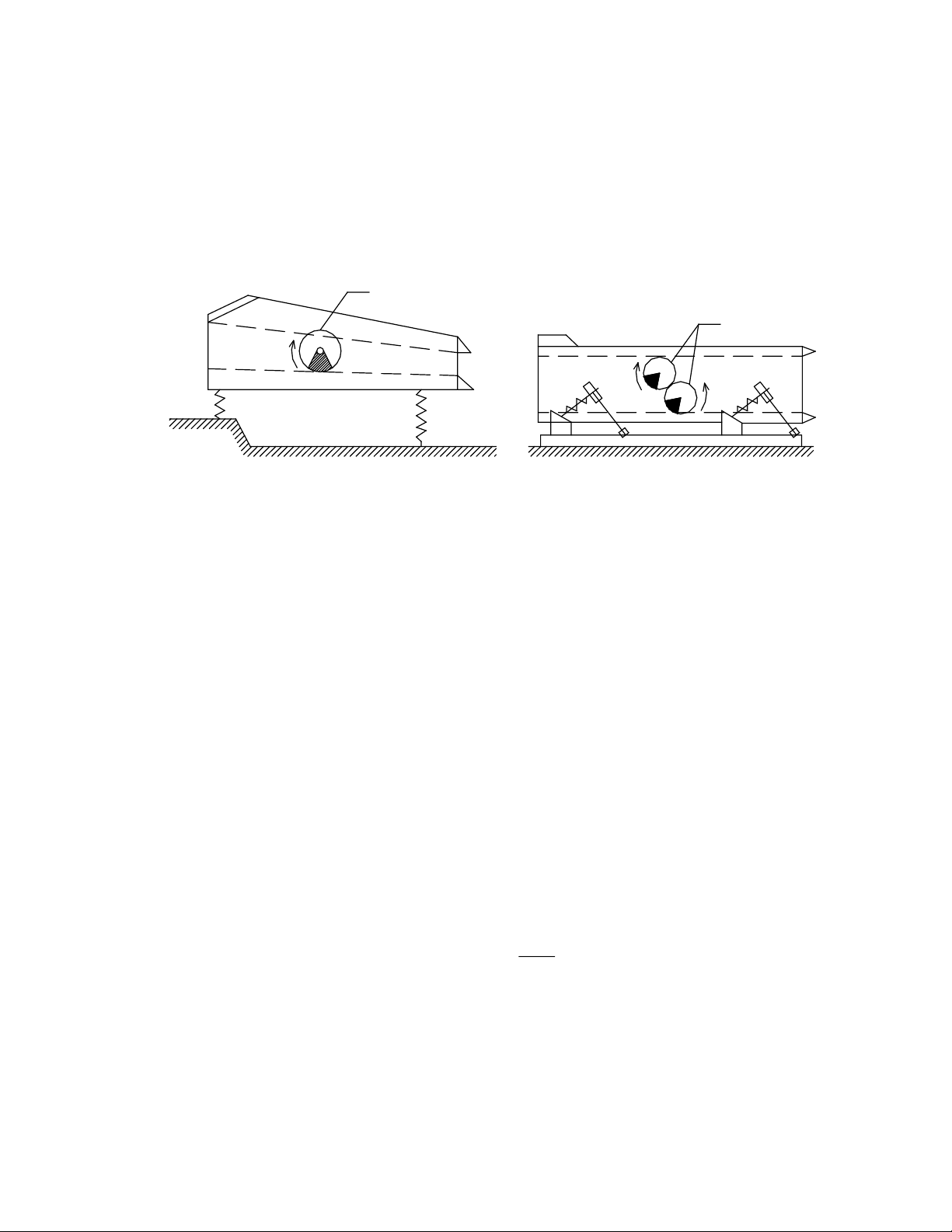
Xét máy sàng rung quán tính như Hình 9-1
Cấu tạo và nguyên lý làm việc đã xét trong môn học “Máy và thiết bịsản
xuất vật liệu xây dựng”. Ở đây, chỉ nêu lại sơ đồ cấu tạo như sau:
9.1.1. Xây dựng mô hình động lực học của máy sàng rung có hướng
Giảthiết:
Bỏqua ảnh hưởng va đập của các hạt vật liệu và có thểcoi khung sàng có
dao động điều hoà.
Có thểcoi 1/3 khối lượng vật liệu trên sàng dao động cùng với sàng
Đường tác dụng của lực kích động đi qua trọng tâm của hệthống
Độ cứng và khả năng chịu tải của các lò xo là như nhau và độ cứng tương
đương là S
Sựdập tắt dao động giữa sàng và dòng vật liệu thểhiện bằng hệsốdập tắt
dao động K
Ký hiệu:
m - khối lượng dao động của toàn hệ
3
m
mm VL
S
m
m
Hình a.
Sàng rung vô hướng
Hình b
. Sàng rung có hướng
Hình 9-1. Sàng rung
http://www.ebook.edu.vn
Với:
mS- Khối lượng dao động của sàng
mVL - Khối lượng vật liệu tổng cộng nằm trên mặt sàng
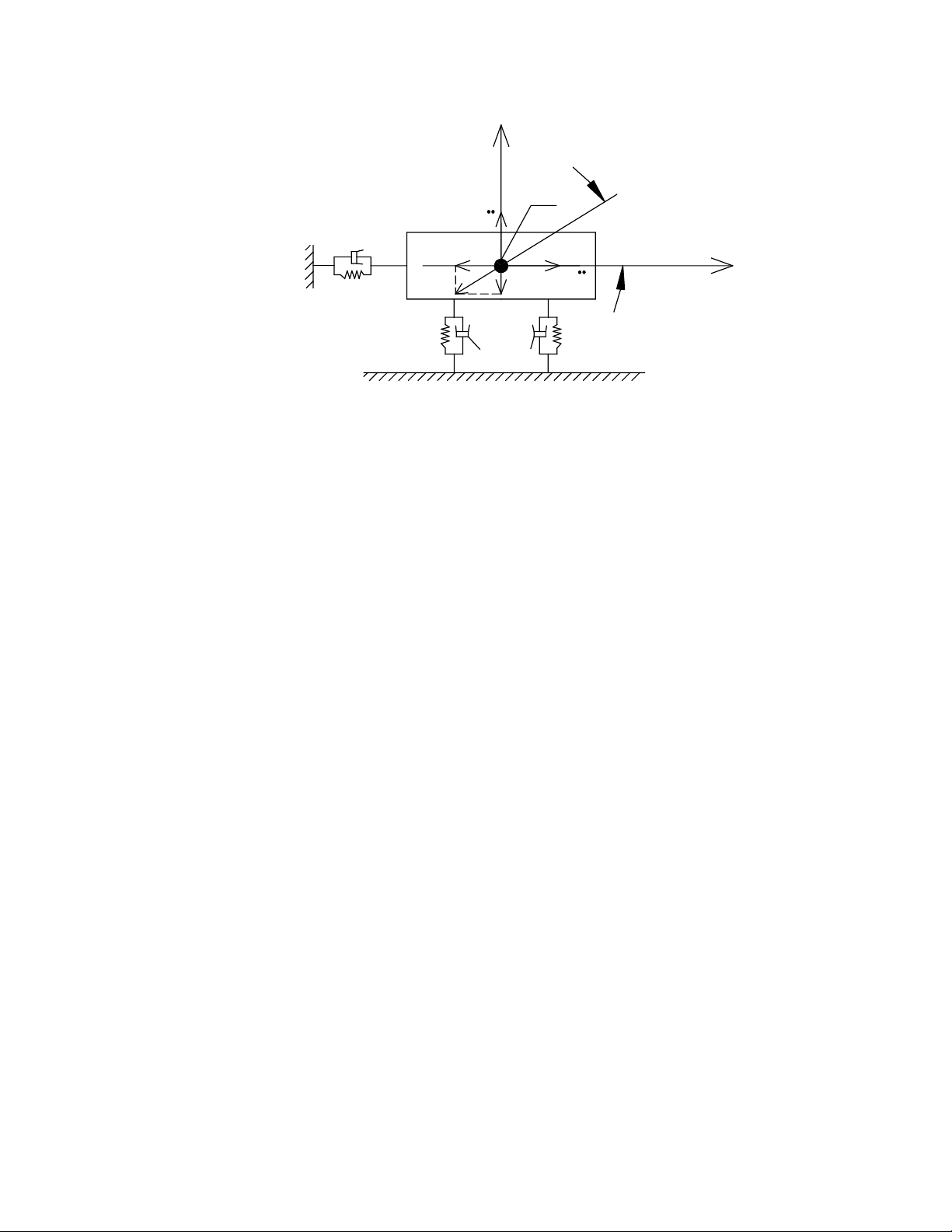
SX, SY-Độ cứng theo phương X, phương Y
KX, KY- Hệsốdập tắt dao động theo X và phương Y
F - lực kích động được phân tích thành FX, FY
- Góc nghiêng của đường tác dụng lực của lực kích động theo phương
ngang
Hệ2 bậc tự do theo 2 phương X và Y
9.1.2. Viết phương trình chuyển động
yyy
XXX
FySyKym
FXSxKxm
(9-1)
Với: tsinrmF 2
00
Trong đó:
m0r0- Mômen khối lượng của các bánh lệch tâm
- Vận tốc góc của bộgây rung
sinFF;cosFF yx
Thay vào chúng ta có:
tsinsinrmySyKym
tsincosrmxSxKxm
2
00xx
2
00xx
(9-2)
y
m
F
x
mx
my
F
y
S
y
/2
S
y
/2 K
y
/2
S
x
K
x
x
F
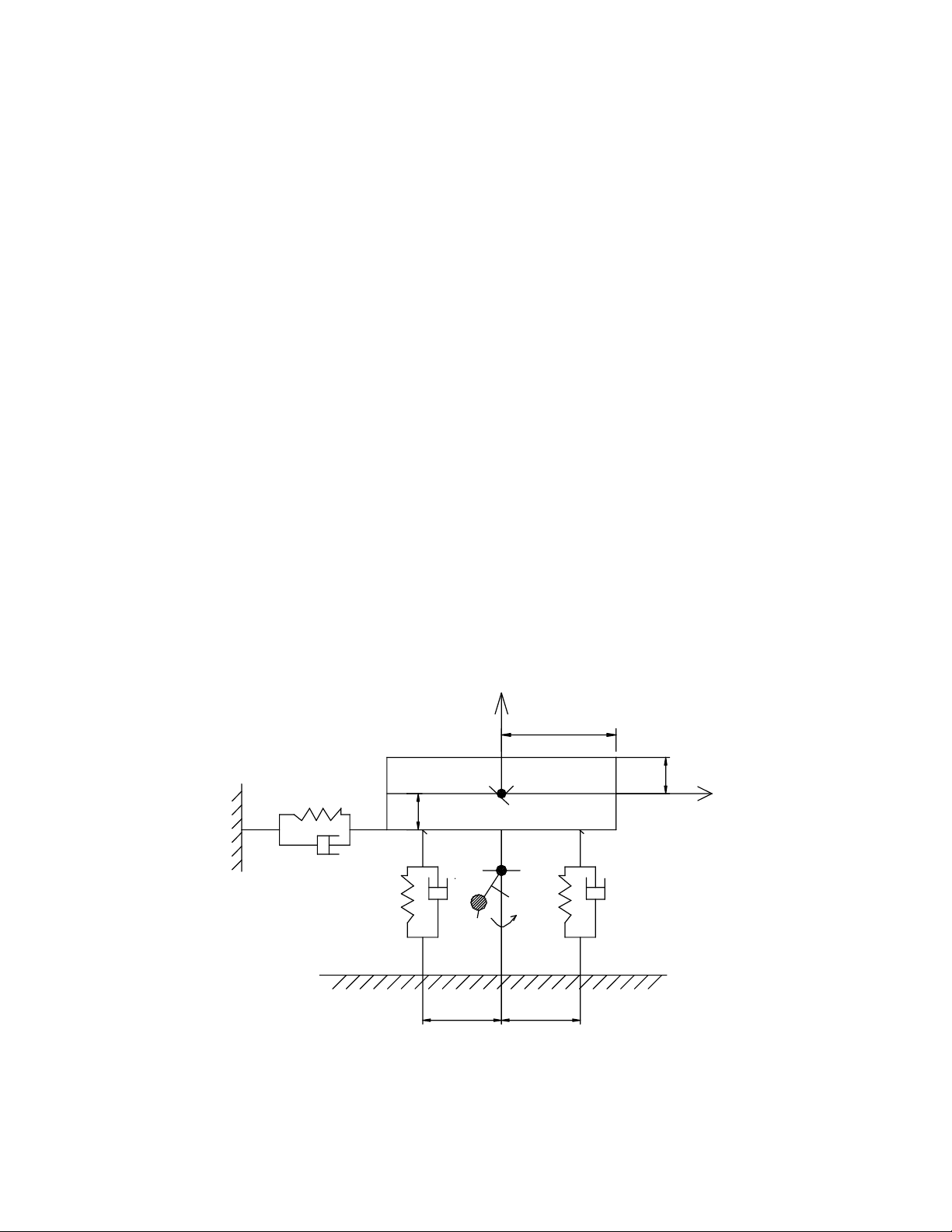
Hình 9-2. Mô hình động lực học
http://www.ebook.edu.vn
9.2. Nghiên cứu dao động của bàn rung đúc bê tông
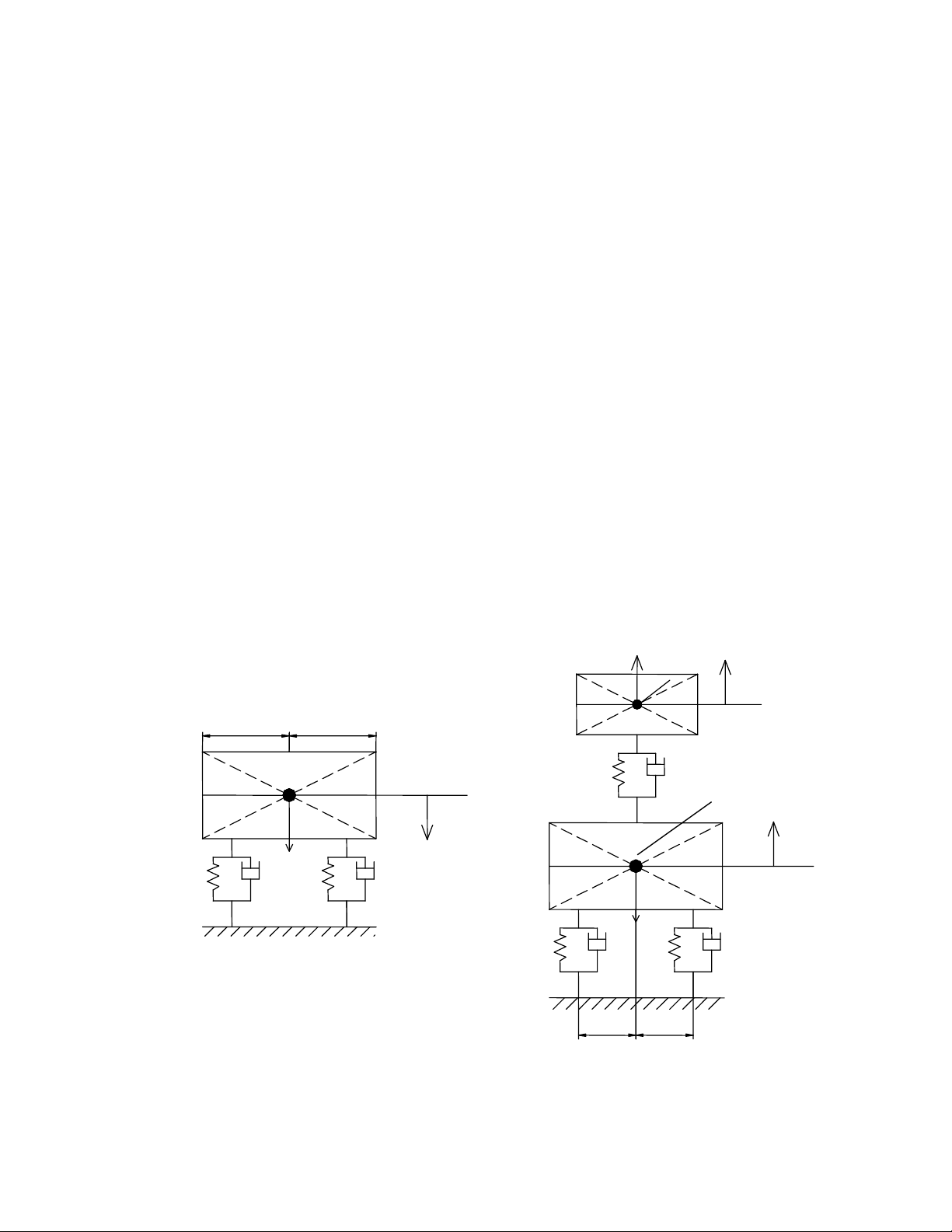
9.2.1. Mô hình động lực học 1 khối lượng (Hình a)
Giảthiết:
- Lực kích động qua trọng tâm hệthống
- Kết cấu hệ đối xứng
- Chỉ xét đến khối lượng của bàn rung
và ván khuân, bỏqua khối lượng bê tông
9.2.2. Mô hình 2 khối lượng (Hình b)
Ký hiệu:
mb- Khối lượng tổng cộng của bê tông
mb’ - Khối lượng một phần bê tông dao
động cùng bàn rung
mv- Khối lượng ván khuôn
ms- Khối lượng các phần dao động thuộc
bàn rung
Trong tính toán gần đúng, khối lượng chung
của hệlà:
'bsv mmmm
Với mb’=(0,2 - 0,35)mb
Trong mô hình này đã đưa vào cả khốilượng của bê tông và độ cứng, hệsố
dập
tắt dao động của bê tông.
Hình 9-3. Các mô hình động lực học
l/2
k/2
S/2
S/2
F
l/2
k/2
y
m
l
l
k/2
S/2
S/2
F
S/2
k/2
k/2
y
a
m
b
y
y
b
m
S
+m
V
http://www.ebook.edu.vn
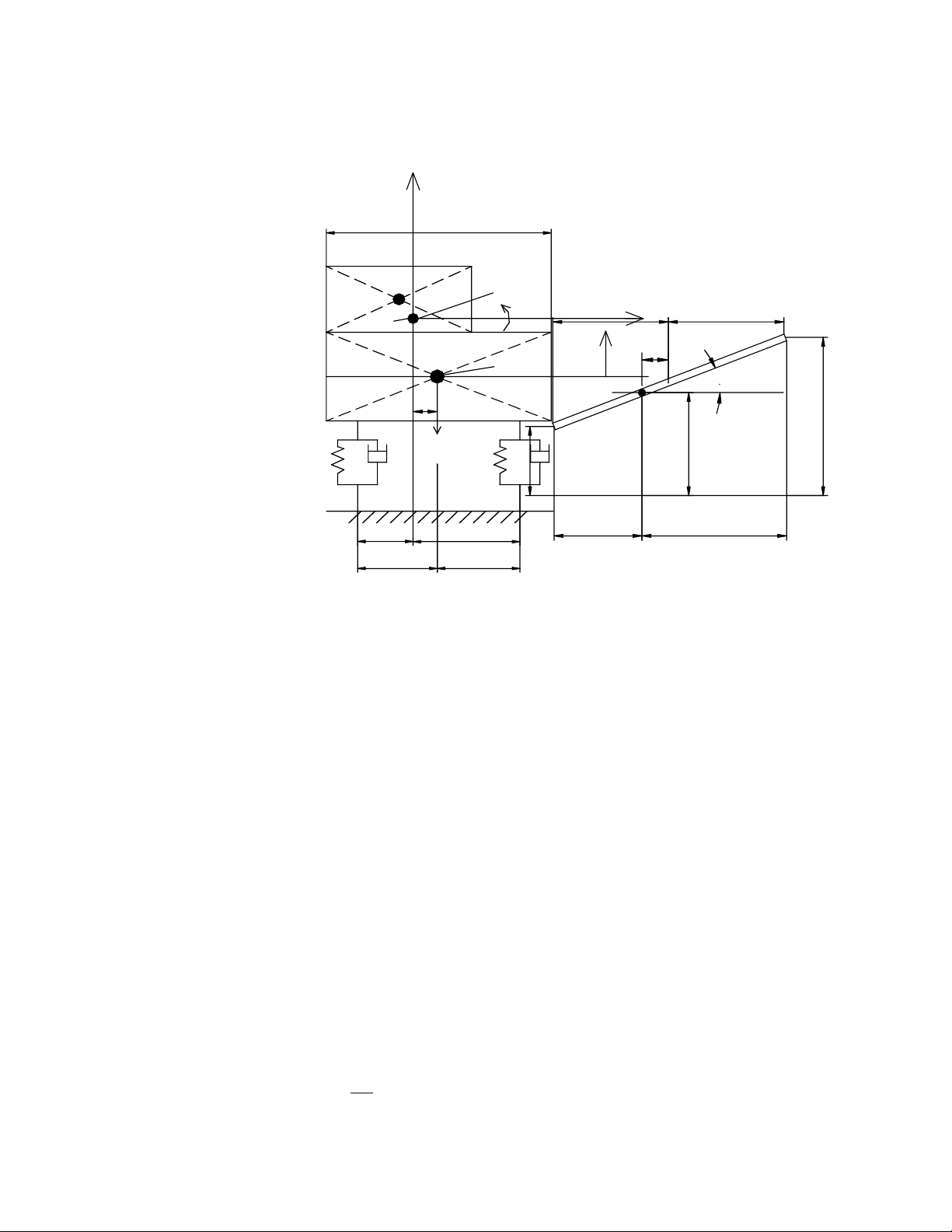
9.2.3. Mô hình động lực học của bàn rung chịu tải không đối xứng
Kết cấu hệ không đối xứng
Ký hiệu:
O - Trọng tâm chung của hệ
m - Khối lượng chung
F.ex- Mômen của lực kích động
Z
- Góc quay của khối lượng m quanh trục vuông góc với mặt phẳng hình
vẽ(trục Z)
ex-Độ lệch tâm của khối lượng chung m với trọng tâm của bàn rung
Phương trình chuyển động:
X111222111222Z
22112211
e.tcosFylSylSylKylK
tcosFySySyKyKym
(9-3)
Với:
Z22
Z11
tglyy
tglyy
Đặt ex=e.l)e1(ll);e1(ll
l
e
e21
X
y - Độ dịch chuyển của trọng tâm
l
l
1
y
1
m
l
2
l
y
2
y
1
2
z
e
x
=el
l
2
B
F
l
l
1
l
S
1
k
1
0
y
S
2
k
2
m
S
m
y
2
x
e
x
(m
y
+m
b'
)
z
12
Hình 9-4. Mô hình động lực học cuả bàn rung khi chưa chịu tải không đối xứng
http://www.ebook.edu.vn
Vì góc lắc Z
nhỏ( 10-3 - 10-4 rad) nên coi
Z
tg .
Thay kết quảtrên vào (1) chúng ta có:
)e1(lyy
)e1(lyy
2
1
Sắp xếp, rút gọn lại chúng ta có:
tcosleFSleyyKle)e1(Sl)e1(Kl
tcosFSleKleSyyKym
2222
(9-4)
Trong đó:
2121 SSS;KKK
Coi: 0lSlS
0lKlK
12
12
Chú ý:
Hệ phương trình (9-3) là phương trình có cảl1, l2, y1, y2, có gắng biến đổi
để đưa về phương trình (9-4) là hệ phương trình chỉcó l, y,
9.2.4. Bàn rung dao động tròn
Khi không thể đặt bộphận gây ra lực kích động vào đúng trọng tâm hệ
thống lúc này mômen của lực kích động làm cho góc lắc của bàn rung thay đổi
một cách điều hoà.
Các điểm của bàn rung dao động trong quá trình làm việc sẽ là điểm có
dao động tổng hợp theo 2 phương (x,y) và góc quay
. Quỹ đạo thực không
phải là đường tròn mà là đường Elip
Ký hiệu:
O0- Trọng tâm của bàn rung có độ dịch chuyển theo 2 phương x, y
Sy/2
d
00
Kx
l
1
Sy/2
Ky/2
mo
r
0
0
1
Sx
m
y
l
Ky/2
2
l
y
x
P
lx
Hình 9-5. Mô hình động lực học của bàn rung dao động tròn