ET 2060 Biểu diễn tín hiệu và hệ thống LTI trên miền tần số ( TS. Đặng Quang Hiếu )

Chia sẻ: Nguyễn Ngọc Minh | Ngày: | Loại File: PDF | Số trang:27

Thêm vào BST

Báo xấu

216
lượt xem 42
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Vai trò của biến đổi Fourier ◮ ◮ Quan trọng trong toán học, vật lý và các ngành kỹ thuật đặc biệt là xử lý tín hiệu. Khái niệm chuỗi Fourier do Joseph Fourier giới thiệu vào năm 1807, và sau đó được phát triển bởi nhiều nhà khoa học nổi tiếng khác. Phân loại: ◮ ◮ ◮ ◮ Chuỗi Fourier (FS) Chuỗi Fourier rời rạc theo thời gian (DTFS) Biến đổi Fourier (FT) Biến đổi Fourier rời rạc theo thời gian (DTFT) ◮ Biến đổi Fourier rời rạc (DFT) có thể được thực hiện nhanh (các thuật toán FFT). Tín hiệu trên miền thời gian và...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: ET 2060 Biểu diễn tín hiệu và hệ thống LTI trên miền tần số ( TS. Đặng Quang Hiếu )

ET 2060 Biểu diễn tín hiệu và hệ thống LTI trên miền tần số TS. Đặng Quang Hiếu http://ss.edabk.org Trường Đại học Bách Khoa Hà Nội Viện Điện tử - Viễn thông 2011-2012 Vai trò của biến đổi Fourier ◮ Quan trọng trong toán học, vật lý và các ngành kỹ thuật đặc biệt là xử lý tín hiệu. ◮ Khái niệm chuỗi Fourier do Joseph Fourier giới thiệu vào năm 1807, và sau đó được phát triển bởi nhiều nhà khoa học nổi tiếng khác. Phân loại: ◮ Chuỗi Fourier (FS) ◮ Chuỗi Fourier rời rạc theo thời gian (DTFS) ◮ Biến đổi Fourier (FT) ◮ Biến đổi Fourier rời rạc theo thời gian (DTFT) ◮ Biến đổi Fourier rời rạc (DFT) có thể được thực hiện nhanh (các thuật toán FFT).
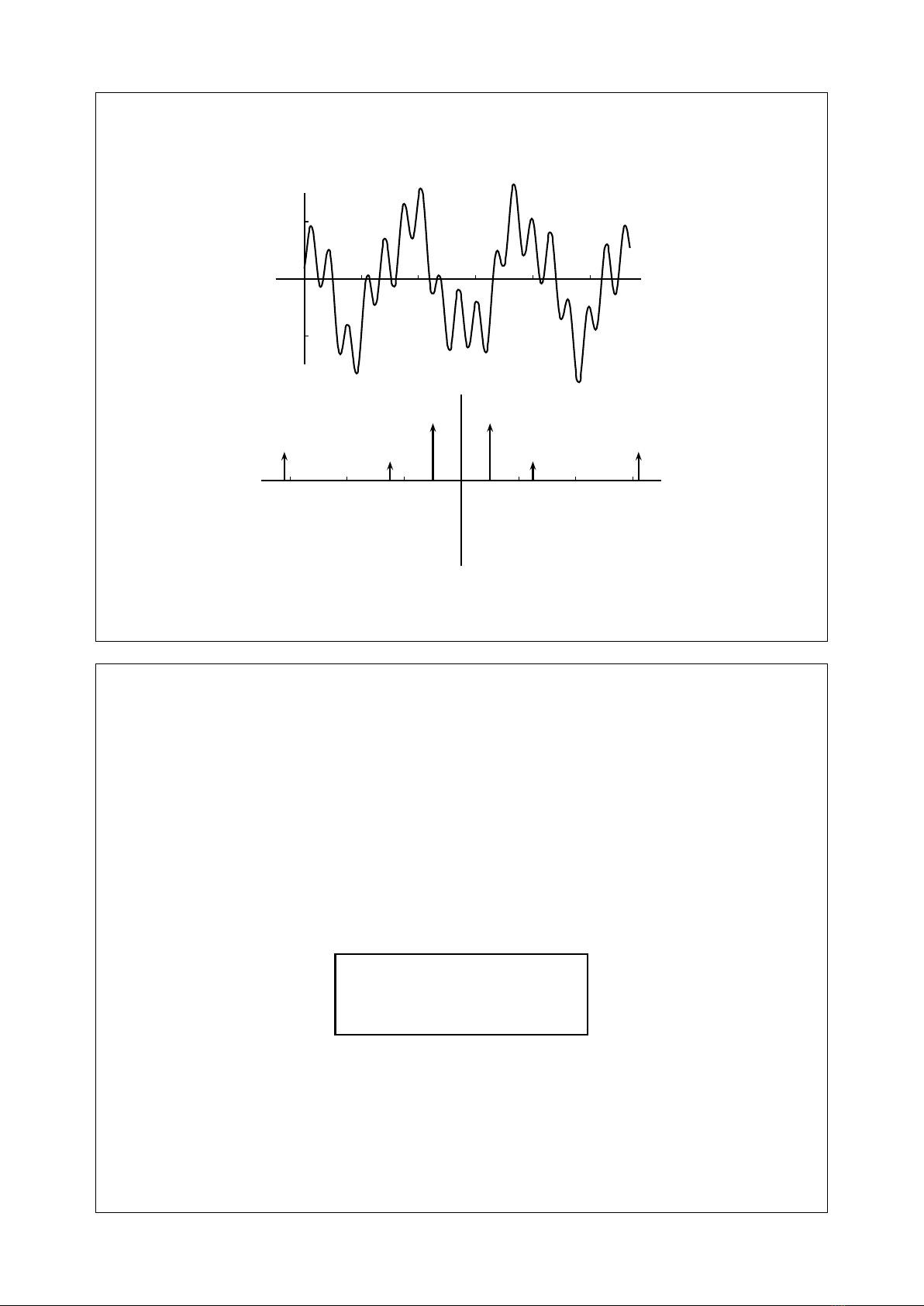
Tín hiệu trên miền thời gian và miền tần số x (t ) 1 t 1 2 3 4 5 -1 |X (f )| -3 -2 -1 1 2 3 f Hàm riêng của hệ thống LTI (1) Xét hệ thống LTI với đầu vào là dãy lũy thừa x [n] = e j ωn ∞ h[k ]e j ω(n−k ) = e j ωn H (e j ω ) y [n] = k =−∞ trong đó, ∞ h[k ]e −j ωk jω H (e ) = k =−∞ e j ωn - hàm riêng (eigenfunction) của hệ thống LTI ◮ H (e j ω ) - trị riêng (eigenvalue) ◮
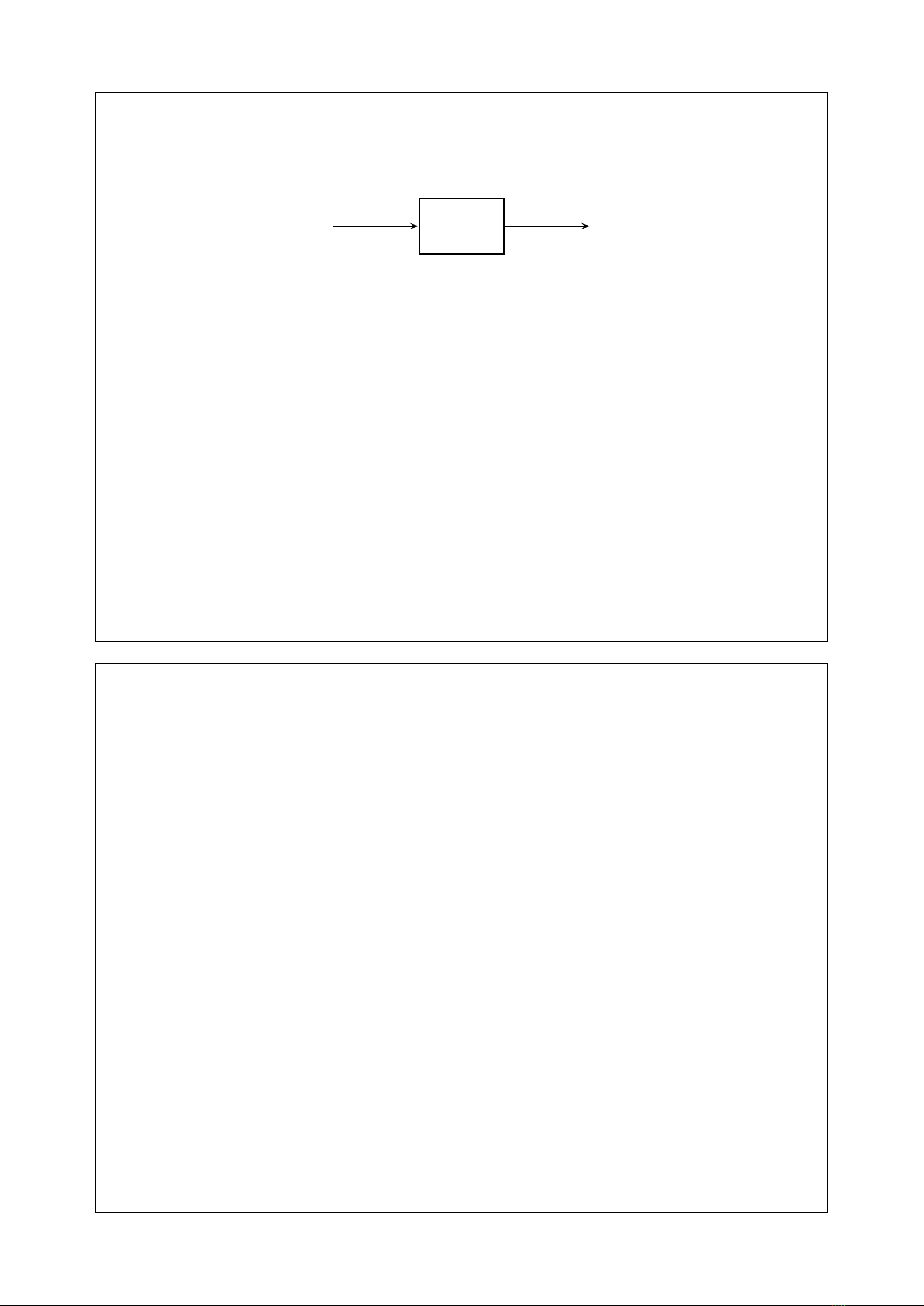
Hàm riêng của hệ thống (2) H (e j ω )e j ω n e j ωn h[n] Nếu biểu diễn đầu vào bất kỳ theo các hàm riêng a k e j ωk n x [n] = k thì ak H (e j ωk )e j ωk n y [n] = k ◮ Không phải thực hiện phép chập!!! H (e j ω ) gọi là đáp ứng tần số của hệ thống ◮ Outline Chuỗi Fourier cho tín hiệu liên tục Chuỗi Fourier cho tín hiệu rời rạc Biến đổi Fourier Biến đổi Fourier rời rạc theo thời gian
Chuỗi Fourier (FS) 2π Tín hiệu x (t ) tuần hoàn với chu kỳ cơ bản T = có thể được Ω0 biểu diễn bởi chuỗi Fourier (FS) như sau: ∞ ck e jk Ω0 t x (t ) = k =−∞ trong đó T 1 x (t )e −jk Ω0 t dt ck = T 0 là các hệ số FS của x (t ) (ck , c−k – thành phần hài bậc |k |). Ví dụ về FS Hãy tìm khai triển chuỗi Fourier cho các tín hiệu sau với chu kỳ cơ bản Ω0 = 2π/T . 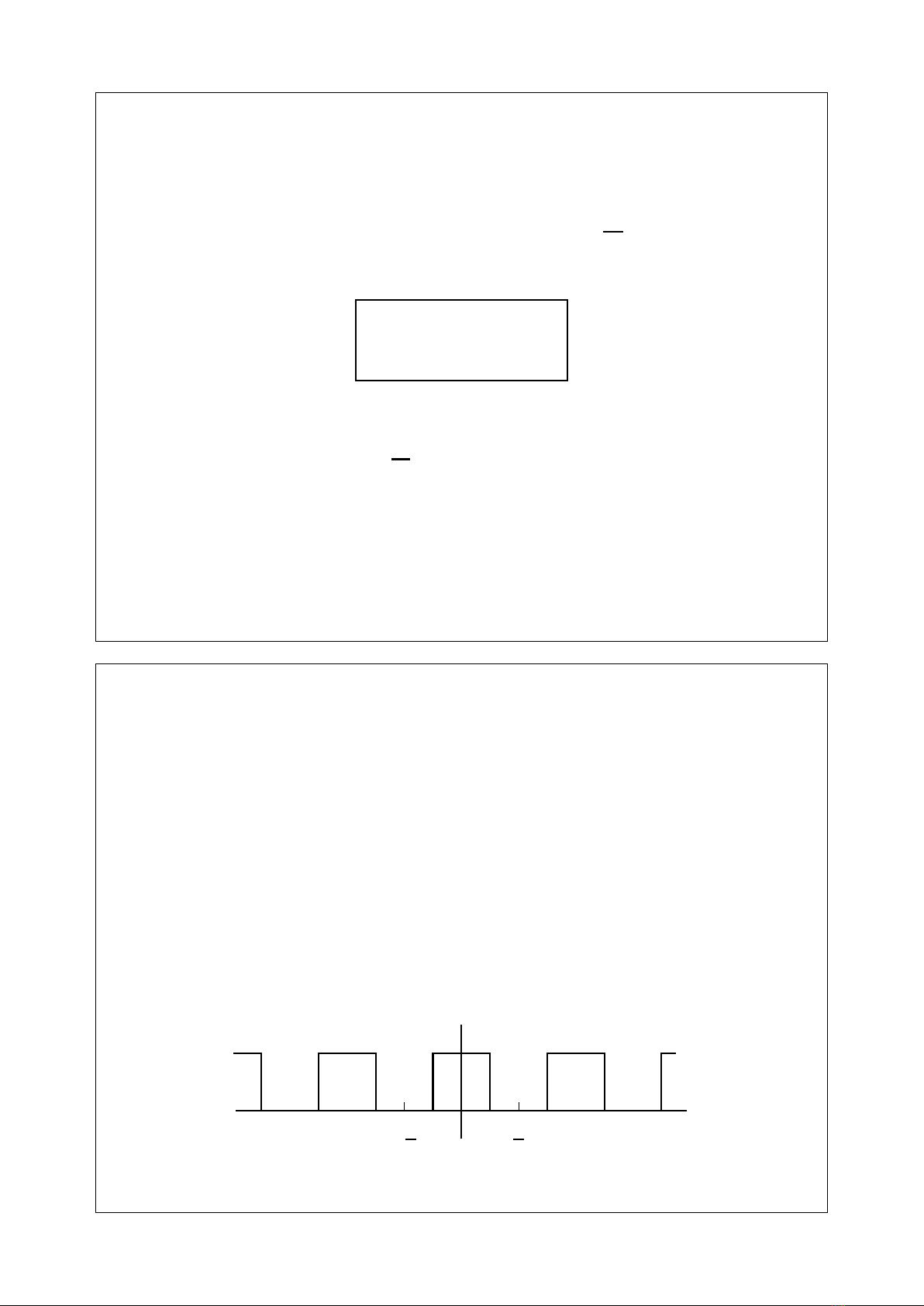(a) x (t ) = cos(Ω0 t ) ∞ − kT ) (b) x (t ) = k =−∞ δ (t (c) Xét trong một chu kỳ, 1, |t | ≤ T0 x (t ) = 0, T0 < |t | < T /2 x (t ) t −T0 T0 −T T 2 2
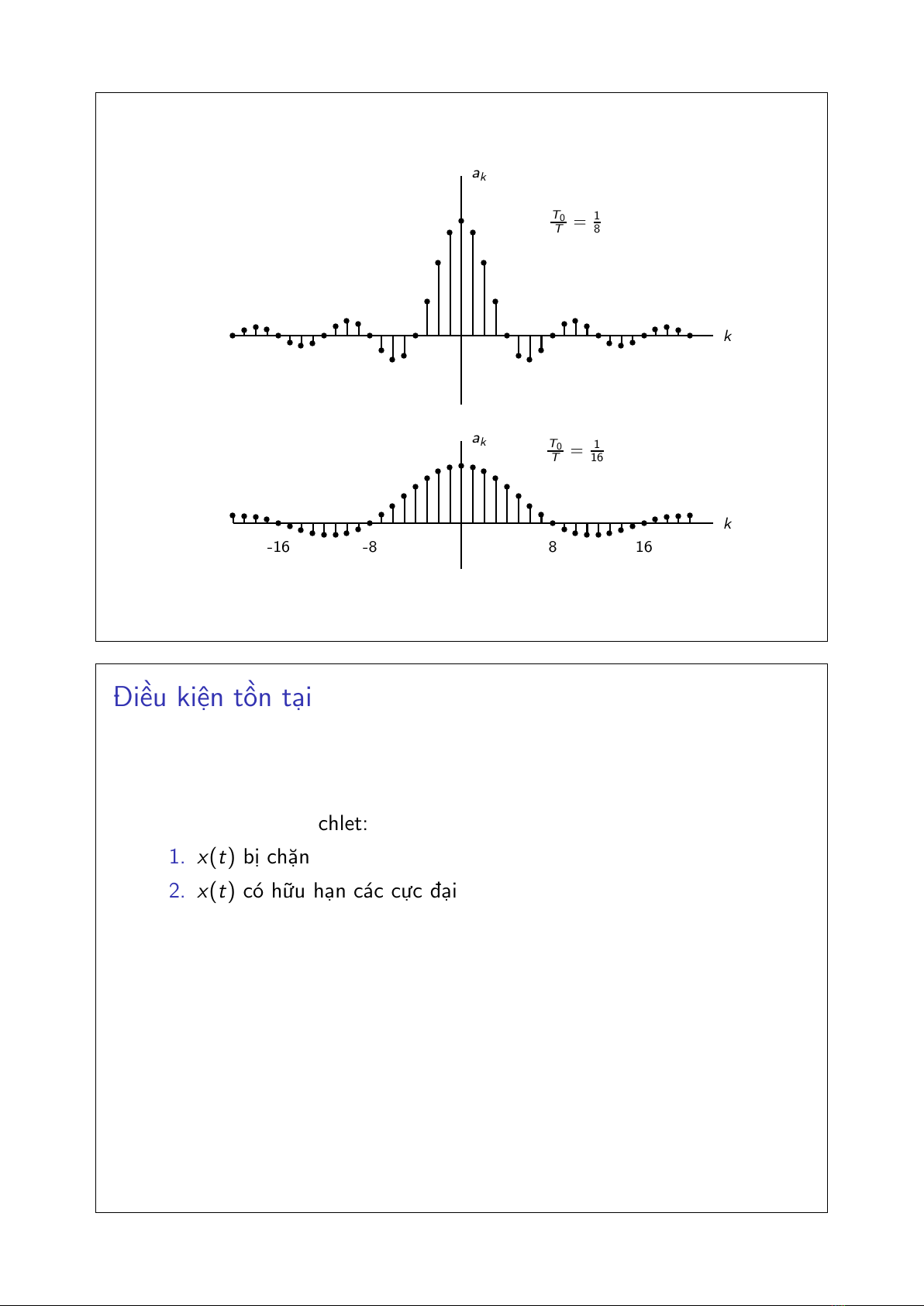
Khai triển chuỗi Fourier của hàm xung vuông tuần hoàn ak T0 1 = 0.25 T 8 k -20 -16 -12 -8 -4 4 8 12 16 20 ak T0 1 = T 16 k -16 -8 8 16 Điều kiện tồn tại FS Các điều kiện Dirichlet: 1. x (t ) bị chặn 2. x (t ) có hữu hạn các cực đại và cực tiểu trong một chu kỳ 3. x (t ) có hữu hạn các điểm gián đoạn trong một chu kỳ Tín hiệu có năng lượng hữu hạn trên một chu kỳ: |x (t )|2 dt < ∞ T
Dạng biểu diễn khác của FS ∞ a0 x (t ) = + ak cos(k Ω0 t ) + bk sin(k Ω0 t ) 2 k =1 Quan hệ giữa ak , bk và ck ? Nếu coi ck là một dãy rời rạc: ∞ X [k ]e jk Ω0 t x (t ) = k =−∞ Tính chất tuyến tính Nếu FS x (t ) ←−→ ak − FS y (t ) ←−→ bk − thì FS αx (t ) + β y (t ) ←−→ αak + β bk −
Tính chất dịch Dịch theo thời gian: FS x (t − t0 ) ←−→ e −j Ω0 t0 ck − Dịch tần số: FS e jk0 Ω0 t x (t ) ←−→ ck −k0 − Ví dụ: Tìm khai triển cho tín hiệu tuần hoàn với chu kỳ T 1, 0 < t ≤ T0 x (t ) = 0, T0 < t < T Đảo trục thời gian FS x (−t ) ←−→ c−k − ◮ Nếu x (t ) chẵn? ◮ Nếu x (t ) lẻ?
Tính chất đối xứng FS ∗ x ∗ (t ) ←−→ c−k − ◮ Nếu x (t ) thực? ◮ Nếu x (t ) ảo? Quan hệ Parseval ∞ 1 2 |ck |2 |x (t )| dt = T T k =−∞ Ý nghĩa: FS bảo toàn công suất của tín hiệu.
Outline Chuỗi Fourier cho tín hiệu liên tục Chuỗi Fourier cho tín hiệu rời rạc Biến đổi Fourier Biến đổi Fourier rời rạc theo thời gian Dãy tuần hoàn và chuỗi Fourier Dãy x [n] (hoặc x [n]N ) tuần hoàn với chu kỳ N : ˜ ˜ ∀n , r ∈ Z x [n] = x [n + rN ], ˜ ˜ Khai triển chuỗi Fourier cho dãy x [n]: ˜ 2π ck e j kn x [n] = ˜ N k 2π Đặc điểm của các thành phần tần số e j kn ∀k ∈ Z? , N 2π 2π ej kn = ej (k +rN )n ∀r ∈ Z , N N N −1 2π X [k ]e j kn x [n] = ˜ X [k ] = ck +rN , N r k =0
Tính X [k ]? 2π (i) Nhân cả hai vế với e −j mn , tính tổng với n = 0, (N − 1) N N −1 N −1 N −1 −j 2π mn 2π (k −m)n X [k ]e j x [n]e ˜ = N N n =0 n =0 k =0 (ii) Đổi thứ tự lấy tổng ở vế phải N −1 N −1 N −1 −j 2π mn 2π (k −m)n ej x [n]e ˜ = X [k ] N N n =0 n =0 k =0 (iii) Tính trực giao: N −1 k − m = rN N , khi 2π (k −m)n ej = N k − m = rN 0, khi n =0 N −1 2π x [n]e −j mn =⇒ = N · X [m] ˜ N n =0 Khái niệm chuỗi Fourier rời rạc N −1 1 2π x [n]e −j kn X [k ] = ˜ N N n =0 ˜ ˜ X [k ] tuần hoàn với chu kỳ N . Ký hiệu: X [k ] hoặc X [k ]N . DTFS (chuỗi Fourier rời rạc theo thời gian) cho dãy tuần hoàn: DTFS ˜ x [n] ←− −→ X [k ] − ˜ N −1 N −1 1 −j 2π kn 2π ˜ ˜ X [k ]e j N kn X [k ] = x [n]e ˜ x [n] = ˜ , N N n =0 k =0 ˜ ◮ Nếu cần nhấn mạnh "hệ số", có thể thay X [k ] bằng ký hiệu ck . ˜ 2π W N = e −j ◮ → công thức? N ˜ ˜ ◮ Khái niệm biên độ và pha: |X [k ]|, arg{X [k ]}.
Ví dụ về DTFS (1) Tìm khai triển Fourier của dãy ∞ ∀r ∈ Z 1, n = rN , δ(n − rN ) = x [n] = ˜ 0, n = rN r =−∞ (2) Cho x [n] là dãy tuần hoàn với chu kỳ N ˜ ∀n ∈ Z, M < N 1, ℓN ≤ n ≤ ℓN + M − 1, x [n] = ˜ 0, n còn lại ˜ ˜ ˜ Hãy tìm X [k ], |X [k ]|, arg{X [k ]}. (3) Dãy x [n] tuần hoàn với chu kỳ N cũng có thể coi là một dãy ˜ ˜ tuần hoàn có chu kỳ 2N . Nếu X1 [k ]N = DTFS{x [n]N } và ˜ ˜2 [k ]2N = DTFS{x [n]2N }. Hãy tính X2 [k ]2N theo X1 [k ]N . ˜ ˜ X ˜ DTFS của dãy xung chữ nhật tuần hoàn N = 100, M = 10 0.1 0.09 0.08 0.07 0.06 |X[k]| 0.05 0.04 0.03 0.02 0.01 0 −100 −80 −60 −40 −20 0 20 40 60 80 100 k 3 2 1 arg{X[k]} 0 −1 −2 −3 −100 −80 −60 −40 −20 0 20 40 60 80 100 k
Các tính chất của chuỗi Fourier rời rạc (1) Tuyến tính: DTFS ˜ ˜ a1 x1 [n]N + a2 x2 [n]N ←− −→ a1 X1 [k ]N + a2 X2 [k ]N − ˜ ˜ (2) Dịch thời gian DTFS 2π kn ˜ ˜ x [n − n0 ] ←− −→ e −j N kn0 X [k ] := WN 0 X [k ] − ˜ (3) Dịch tần số DTFS ˜ 2π ej kn x [n] ←− −→ X [k − k0 ] − ˜ N0 Tính chất đối ngẫu Nếu DTFS ˜ x [n] ←− −→ X [k ] − ˜ thì DTFS 1 ˜ X [n] ←− −→ x [−k ] − ˜ N Ví dụ: Cho ∞ ˜ δ(k − rN ) X [k ] = r =−∞ Hãy tìm x [n]? ˜
Các tính chất đối xứng DTFS ˜ (a) x ∗ [n] ←− −→ X ∗ [−k ] − ˜ DTFS ˜ (b) x [−n] ←− −→ X ∗ [k ] − ˜ DTFS 1 ˜ ˜ (c) Re[˜ [n]] ←− −→ 2 [X [k ] + X ∗ [−k ]] − x DTFS ˜ (d) 1 [˜ [n] + x ∗ [−n]] ←− −→ Re[X [k ]] − 2x ˜ (e) Khi x [n] ∈ R ˜ ˜ ˜ X [k ] = X ∗ [− k ] ◮ ˜ ˜ Re[X [k ]] = Re[X [−k ]] ◮ ˜ ˜ Im[X [k ]] = −Im[X [−k ]] ◮ ˜ ˜ ◮ | X [ k ] | = |X [ − k ] | ˜ ˜ ◮ arg{X [k ]} = − arg{X [−k ]} Chập tuần hoàn Cho DTFS ˜ x1 [n] ←− −→ X1 [k ] − ˜ DTFS ˜ x2 [n] ←− −→ X2 [k ] − ˜ ˜ ˜ ˜ Nếu X3 [k ] = X1 [k ]X2 [k ] thì x3 [n] =? ˜ ⇒ Khái niệm chập tuần hoàn: N −1 1 1 ∗˜ x1 [m]˜2 [n − m] x3 [n]N = x1 [n](˜)N x2 [n] = ˜ ˜ ˜ x N N m =0 Chứng minh?
Cách tính chập tuần hoàn Tìm x3 (n0 ) với n0 ∈ [0, (N − 1)] ˜ (1) Lấy đối xứng qua trục tung x2 [m] → x2 [−m] ˜ ˜ (2) Dịch theo trục hoành n0 mẫu (3) Nhân hai dãy vn0 [m] = x1 [m]˜2 [n0 − m] trong đoạn [0, (N − 1)] ˜ ˜ x (4) Tính tổng các phần tử của dãy vn0 [m] trong đoạn [0, (N − 1)] ˜ → x3 [n0 ] ˜ ∀r ∈ Z. (5) Dãy tuần hoàn chu kỳ N : x3 [n0 ] = x3 [n0 + rN ], ˜ ˜ Các tính chất khác ◮ Tích của hai dãy? ◮ Tương quan tuần hoàn của hai dãy? Tự đọc!
Bài tập Cho tín hiệu liên tục (tuần hoàn) xc (t ) có khai triển Fourier như sau: 9 −3 ak e j 2πkt /10 xc (t ) = k =−9 trong đó các hệ số ak = 0, ∀|k | > 9. Tín hiệu này được lấy mẫu 1 với chu kỳ T = 6 10−3 [s] để tạo thành dãy x [n] = xc (nT ). (a) Dãy x [n] có tuần hoàn không, nếu có thì chu kỳ bao nhiêu? ˜ (b) Hãy tính X [k ] theo các hệ số ak . Outline Chuỗi Fourier cho tín hiệu liên tục Chuỗi Fourier cho tín hiệu rời rạc Biến đổi Fourier Biến đổi Fourier rời rạc theo thời gian
Biến đổi Fourier (FT) cho tín hiệu không tuần hoàn Xét x (t ) là tín hiệu liên tục và không tuần hoàn theo thời gian. Nếu coi x (t ) là tuần hoàn với T → ∞, ta có cặp biến đổi Fourier: FT t Ω FT−1 FT x (t ) ←−→ X (j Ω) − trong đó: ∞ x (t )e −j Ωt dt X (j Ω) = FT{x (t )} = −∞ và ∞ 1 −1 X (j Ω)e j Ωt d Ω x (t ) = FT {X (j Ω)} = 2π −∞ Điều kiện tồn tại FT ∞ −∞ |x (t )|dt T0 (d) x (t ) = cos(Ω0 t )
FT cho tín hiệu tuần hoàn Xét tín hiệu ở miền tần số X (j Ω) = 2πδ(Ω − Ω0 ), ta có: ∞ 1 2πδ(Ω − Ω0 )e j Ωt d Ω x (t ) = 2π −∞ j Ω0 t =e =⇒ Nếu biết FS của x (t ) (tuần hoàn), tìm FT? Ví dụ: Tìm FT của các tín hiệu sau (a) x (t ) = cos(Ω0 t ) ∞ − kT ) (b) x (t ) = k =−∞ δ (t (c) Xét trong một chu kỳ, 1, |t | ≤ T0 x (t ) = 0, T0 < |t | < T /2 Các tính chất của biến đổi Fourier (1) Tuyến tính FT a1 x1 (t ) + a2 x2 (t ) ←−→ a1 X1 (j Ω) + a2 X2 (j Ω) − (2) Dịch thời gian FT x (t − t0 ) ←−→ e −j Ωt0 X (j Ω) − (3) Dịch tần số FT e j Ω0 t x (t ) ←−→ X (j (Ω − Ω0 )) −
Tính chất đối xứng FT x ∗ (t ) ←−→ X ∗ (−j Ω) − ◮ Khi x (t ) thực / ảo? Nếu x (t ) thực và x (t ) = xe (t ) + xo (t ), hãy tìm FT của xe (t ) ◮ và của xo (t )? Vi phân và tích phân Vi phân: FT d x (t ) ←−→ j ΩX (j Ω) − dt Tích phân: t FT 1 x (τ )d τ ←−→ − X (j Ω) + π X (0)δ(Ω) jΩ −∞ Ví dụ: Tìm FT của dãy nhảy đơn vị u (t ).
Co dãn trên miền thời gian và tần số FT 1 jΩ x (at ) ←−→ − X( ) |a| a với a ∈ R, const. Đối ngẫu Nếu FT x (t ) ←−→ X (j Ω) − thì FT X (jt ) ←−→ 2π x (−Ω) −
Quan hệ Parseval ∞ ∞ 1 2 |X (j Ω)|2 d Ω |x (t )| dt = 2π −∞ −∞ Chập trên miền thời gian FT y (t ) = x (t ) ∗ h(t ) ←−→ Y (j Ω) = X (j Ω)H (j Ω) − ◮ H (j Ω) - đáp ứng tần số của hệ thống LTI. ◮ Khi hệ thống LTI không ổn định, có tồn tại H (j Ω) không? Tự đọc thêm về FT của tích, tương quan chéo giữa hai tín ◮ hiệu.