Group FB: TEAM TOÁN VD–VDC
Hãy tham gia nhóm STRONG TEAM TOÁN VD-VDC để cùng học và cùng làm- Nhóm của các Gv, Sv toán 1
Mail: hoainlht@gmail.com
Câu 1: Cho hàm số
2
2 3 3y x x x
có đồ thị (C). Mệnh đề nào dưới đây đúng?
A.
()C
cắt trục hoành tại hai điểm phân biệt
B.
()C
cắt trục hoành tại hai điểm phân biệt
C.
()C
không cắt trục hoành
D.
()C
cắt trục hoành tại 1 điểm phân biệt
Lời giải
Chọn D
Phương trình hoành độ giao điểm
2
2
2
2 3 3 0 3 3 0
x
x x x xx

2x
Vậy (C) cắt trục hoành tại 1 điểm.
FB:Hoài Lệ
Câu 2: Đường cong trong hình sau là đồ thị của hàm số nào dưới đây?
Group FB: TEAM TOÁN VD–VDC
Hãy tham gia nhóm STRONG TEAM TOÁN VD-VDC để cùng học và cùng làm- Nhóm của các Gv, Sv toán 2
A.
2
24
x
yx

. B.
23
2
x
yx
. C.
1
2
x
yx

. D.
3
24
x
yx

.
Lời giải
Tác giả: Đỗ Tấn Bảo Email: Tanbaobg@gmail.com
Chọn A
Dựa vào hình vẽ, đồ thị hàm số đã cho có đường tiệm cận đứng và đường tiệm cận ngang lần
lượt là
và
1
2
y
nên chỉ phương án A và D thỏa mãn.
Vì đồ thị cắt trục tung tại điểm có tung độ dương nên chọn A.
Email: Duyhungprudential@gmail.com
Câu 3. Cho hàm số
fx
có đạo hàm
23
' 1 2 2 3f x x x x
. Tìm số điểm cực trị của
fx
A . 0 B. 3 C. 2 D. 1
Lời giải
Tác giả : Đặng Duy Hùng và Facebook : Duy Hùng
Chọn C
Cho
1
3
'0 2
2
x
f x x
x


Vì
1x
là nghiệm bội chẵn nên qua -1 thì
'fx
không đổi dấu . Vậy hàm số chỉ có 2 điểm
cực trị là
3
2, 2
xx
Boigiabao98@gmail.com
Câu 4. Với giá trị nào của
m
thì đồ thị hàm số
2
2 6 4
2
x mx
ymx
đi qua điểm
(1; 4)A
?
A.
1m
. B.
1
2
m
. C.
1m
. D.
2m
.
Lời giải
Tác giả : Nguyễn Quang Huy, FB: Nguyễn Quang Huy
Chọn A
Group FB: TEAM TOÁN VD–VDC
Hãy tham gia nhóm STRONG TEAM TOÁN VD-VDC để cùng học và cùng làm- Nhóm của các Gv, Sv toán 3
Đồ thị hàm số đi qua điểm
(1; 4)A
2
2.( 1) 6 .( 1) 4
4.( 1) 2
m
m
4(2 ) 6 6mm
1m
Vậy
1m
nên ta chọn đáp án A
thuhangnvx@gmail.com
Câu 5: Cho hàm số:
y f x
xác định và liên tục trên khoảng
3;2
,
2
3
lim 5, lim 3
x
x
f x f x


và có bảng biến thiên như sau
x
3
1
1
2
y'
0
0
y
0
3
5
2
Mệnh đề nào dưới đây sai ?
A. Hàm số không có giá trị nhỏ nhất trên khoảng
3;2
B. Giá trị cực tiểu của hàm số bằng
2
C. Giá trị cực đại của hàm số bằng
0
D. Giá trị lớn nhất của hàm số trên khoảng
3;2
bằng
0
Lời giải
Tác giả: Phùng Thị Thu Hằng, FB: Phùng Hằng
Chọn D
trantuananh12a3@gmail.com
Câu 6. Cho hàm số
y f x
có đồ thị như sau . Hàm số
y f x
đồng biến trên khoảng nào dưới đây ?
3
1
1
1
2
O
x
y
2
Group FB: TEAM TOÁN VD–VDC
Hãy tham gia nhóm STRONG TEAM TOÁN VD-VDC để cùng học và cùng làm- Nhóm của các Gv, Sv toán 4
A.
2; 1
. B.
1;2
. C.
1;1
. D.
2;1
.
Lời giải
Tác giả : Trần Tuấn Anh , FB: Trần Tuấn Anh
Chọn A
leducthien.1991@gmail.com
Câu 7. Kết luận nào sau đây về tính đơn điệu của hàm số
21
1
x
yx
là đúng?
A. Hàm số nghịch biến trên các khoảng
;1
và
1; 
.
B. Hàm số luôn luôn nghịch biến trên
\1
.
C. Hàm số đồng biến biến trên các khoảng
;1
và
1; 
.
D. Hàm số luôn luôn đồng biến biến trên
\1
.
Lời giải
Tác giả : Lê Đức Thiện, FB: Leo
Chọn C
Hàm số
21
1
x
yx
TXĐ:
; 1 1;D
2
1
'0
1
y
x

; 1 1;x
Hàm số đồng biến trên các khoảng
;1
và
1; 
.
tuluc0201@gmail.com
Câu 8. Gọi
,MN
là các điểm cực tiểu của đồ thị hàm số
42
183
4
y x x
. Độ dài đoạn thẳng
MN
là
A.10. B.6. C.8. D.4.
Lời giải
Tác giả : Võ Tự Lực, FB: Võ Tự Lực
Chọn C.
Ta có:
3
0
' 16 ; ' 0 4
4
x
y x x y x
x
.
Bảng xét dấu:
Group FB: TEAM TOÁN VD–VDC
Hãy tham gia nhóm STRONG TEAM TOÁN VD-VDC để cùng học và cùng làm- Nhóm của các Gv, Sv toán 5
x

-4 0 4

'y
- 0 + 0 - 0 +
Dựa vào bảng xét dấu, ta thấy hàm số đạt giá trị cực tiểu tại
4x
và
4x
.
+ Khi
4 61 4; 61x y M
.
+ Khi
4 61 4; 61x y N
.
Vậy
| 4 4 | 8MN
.
Ducchinh2308@gmail.com
Câu 9. Số đường tiệm cận của đồ thị hàm số
1
1
x
yx
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Tác giả : Huỳnh Đức Chính, FB: Huỳnh Đức Chính
Chọn B
Đồ thị của hàm số có tiệm cận đứng
1x
và tiệm cận ngang
1y
nên có 2 đường tiệm
cận.
diemhangtole@gmail.com
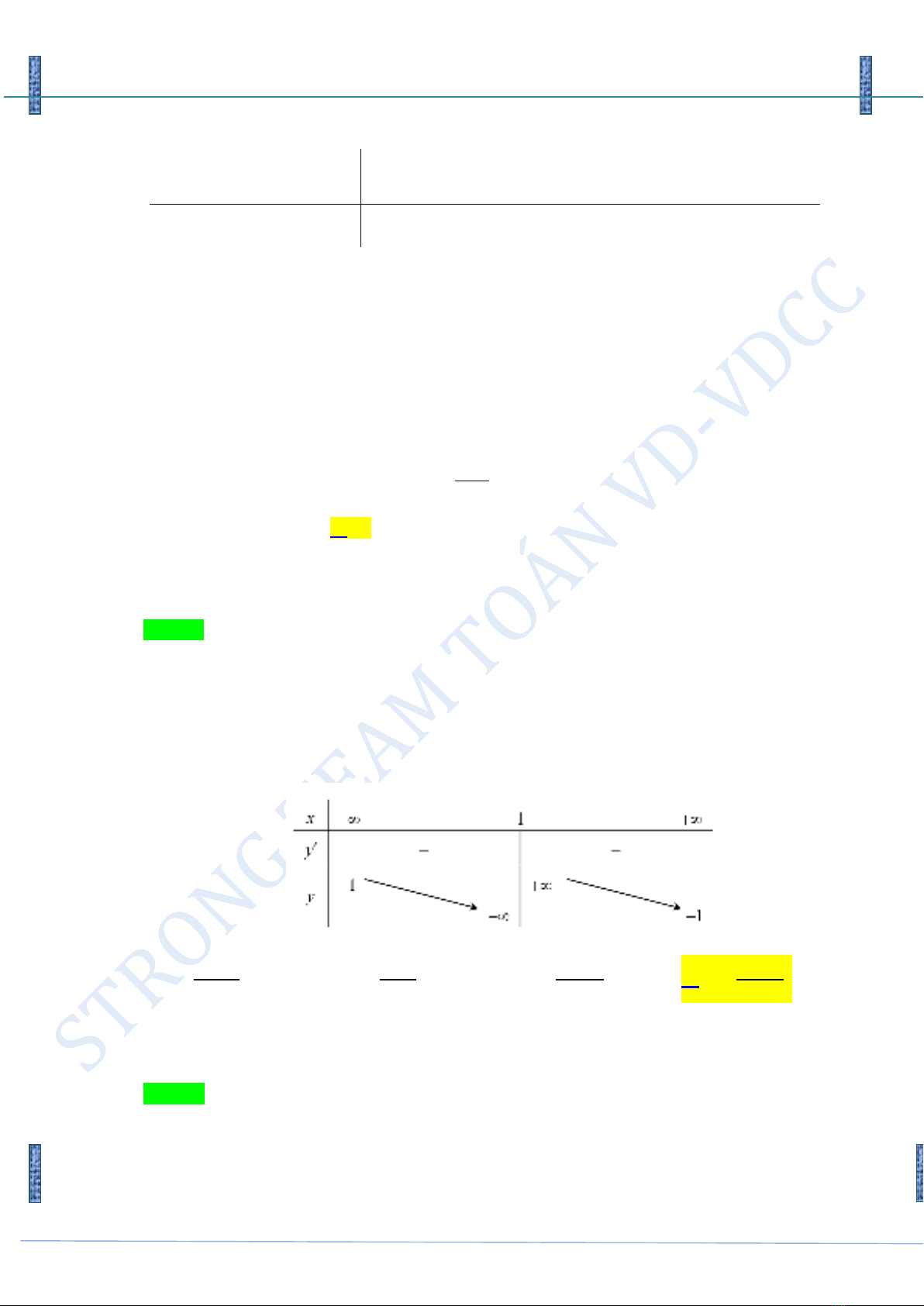
Câu 10. Bảng biến thiên trong hình dưới là của hàm số nào trong các hàm số đã cho?
A.
3
1
x
yx

. B.
3
1
x
yx
. C.
2
1
x
yx

. D.
3
1
x
yx

.
Lời giải
Tác giả : Tô Lê Diễm Hằng, FB: Tô Lê Diễm Hằng
Chọn D
Ta có
1
lim ; lim 1
x
x
yy


suy ra đồ thị hàm số nhận đường thẳng
1y
làm tiệm cận
ngang và đường thẳng
1x
làm tiệm cân đứng.