
GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ
NHẤT CỦA HÀM SỐ
I/ Mục tiêu:
1/ Kiến thức:
+ Nắm được khái niệm về giá trị min, max của hàm số trên tập D (
D
Ì
¡
)
+ Biết dùng công cụ đạo hàm để tìm min, max.
2/ Kỹ năng:
+ Thành thạo việc lập bảng biến thiên của hàm số trên tập D và theo dõi giá trị của hàm số
biến đổi trên D để tìm min, max.
+ Vận dụng tốt quy tắc tìm min, max của hàm số trên đoạn [a; b]
3/ Tư duy, thái độ:
+ Vận dụng linh hoạt các phương pháp phù hợp cho từng bài toán cụ thể.
+ Khả năng nhìn nhận quy các bài toán thực tiễn về tìm min, max.
II/ Chuẩn bị của GV & HS:
+ GV: Giáo án đầy đủ, bảng phụ (Vd 1 SGK)
+ HS: Cần xem lại qui trình xét chiều biến thiên hàm số, SGK, sách bài tập.
III/ Phương pháp: Đàm thoại, gợi mở, nêu vấn đề.
IV/ Tiến trình tiết dạy:
1/ Ổn định tổ chức:
2/ Kiểm tra bài cũ: (5’)

Hỏi: Xét chiều biến thiên của h/s
1
( )
1
y f x x
x
= = +
-
3/ Bài mới:
HĐ1: Xây dựng khái niệm về giá trị min, max của h/s trên tập hợp D.
Tg
HĐ của GV HĐ của HS Ghi bảng
3’
Bài toán: Xét h/s
2
( ) 9
y f x x
= = -
+ Tìm TXĐ của h/s
+ Tìm tập hợp các giá trị của y
+ Chỉ ra GTLN, GTNN của y
GV nhận xét đi đến k/n min,
max
a/ D= [ -3 ; 3]
b/
0 3
y
£ £
c/ + y = 0 khi x = 3 ho
ặc
x = - 3
+ y= 3 khi x = 0
a/ H/s xđ 2
9 0
x
Û - ³
3 3
x
Û - £ £
D= [-3;3]
b/
x D
" Î
ta có:
2
0 9 9
x
£ - £
0 3
y
Þ £ £
1/ Định nghĩa: SGK
0 0
max ( )
( )
/ ( )
x D
M f x
f x M x D
x D f x M
Î
=
ì £ " Î
ï
ï
Ûí$ Î =
ï
ï
î
0 0
min ( )
( )
/ ( )
x D
m f x
f x m x D
x D f x m
Î
=
ì ³ " Î
ï
ï
Ûí$ Î =
ï
ï
î
HĐ 2: Dùng bảng biến thiên của h/s để tìm min, max.
Tg HĐ của GV HĐ của HS Ghi bảng
7’
Từ đ/n suy ra để tìm min,
max của h/s trên D ta cần
theo dõi giá trị của h/s với
x D
Î
. Muốn vậy ta phải
xét sự biến thiên của h/s
trên tập D.
+ Tìm TXĐ
+ Tính y’
Vd1:
D= R
y’ = -2x + 2; y’ =0 x=1
x
y’
- ¥
+ ¥
1
+ 0
-
8’
Vd1: Tìm max, min của
h/s 2
2 3
y x x
= - + +
Vd2: Cho y = x3 +3x2 + 1
a/ Tìm min, max của y
trên [-1; 2)
b/ Tìm min, max của y
trên [- 1; 2]
Tổng kết: Phương pháp
tìm min, max trên D
+ Xét sự biến thiên của
h/s trên D, từ đó
Þ
min,
max
+ Xét dấu y’ => bbt
+ Theo dõi giá trị của y
KL min, max.
Tính y’
+ Xét dấu y’
+ Bbt => KL
max 4
x R
y
Î
=
khi x=1
h/s không có giá trị min trên R
Vd2: y’ = 3x2 + 6x
y’ =0
0
2
x
x
=
é
ê
= -
ê
ë
a/
[ )
1;2
min 1 0
x
y khi x
Î -
= =
Không tồn tại GTLN của h/s
trên [-1;2)
b/
[ ]
1;2
[-1;2]
max 21 2
min 1 0
x
x
y khi x
y khi x
Î -
Î
= =
= =
HĐ 3: Tìm min, max của h/s y = f(x) với x
Î
[a;b]
Tg HĐ của GV HĐ của HS Ghi bảng
Dẫn dắt:
Từ vd2b => nhận xét nếu hs liên
tục trên [a;b] thì luôn tồn tại min,
max trên [a;b] đó. Các giá trị này
+ Tính y’
+ Tìm x0
Î
[a;b] sao cho
f’(x0)=0 hoặc h/s không có
Quy tắc:
SGK trang 21
x
y’
y
+ ¥
-
1
+
-
-
3
- ¥
-
2
0
2
0 0 + +
21
1
10’
đạt được tại x0 có thể là tại đó
f(x) có đạo hàm bằng 0 hoặc
không có đạo hàm, hoặc có thể là
hai đầu mút a, b của đoạn đó.
Như thế không dùng bảng biến
thiên hãy chỉ ra cách tìm min,
max của y = f(x) trên [a;b]
VD: Cho y = - x4 +2x2 +1
Tìm min, max của y trên [0;3]
đạo hàm tại x0
+ Tính f(a), f(b), f(x0)
min, max
+tính y’
+ y’=0
0
1
1 [0;3]
x
x
x
é=
ê
ê
Û =
ê
ê= - Ï
ê
ë
+ Tính f(0); f(1); f(3)
+ KL
Gọi hs trình bày lời
giải trên bảng
HĐ 4: Vận dụng việc tìm min, max để giải quyết các bài toán thực tế
Tg HĐ của GV HĐ của HS Ghi bảng
10’
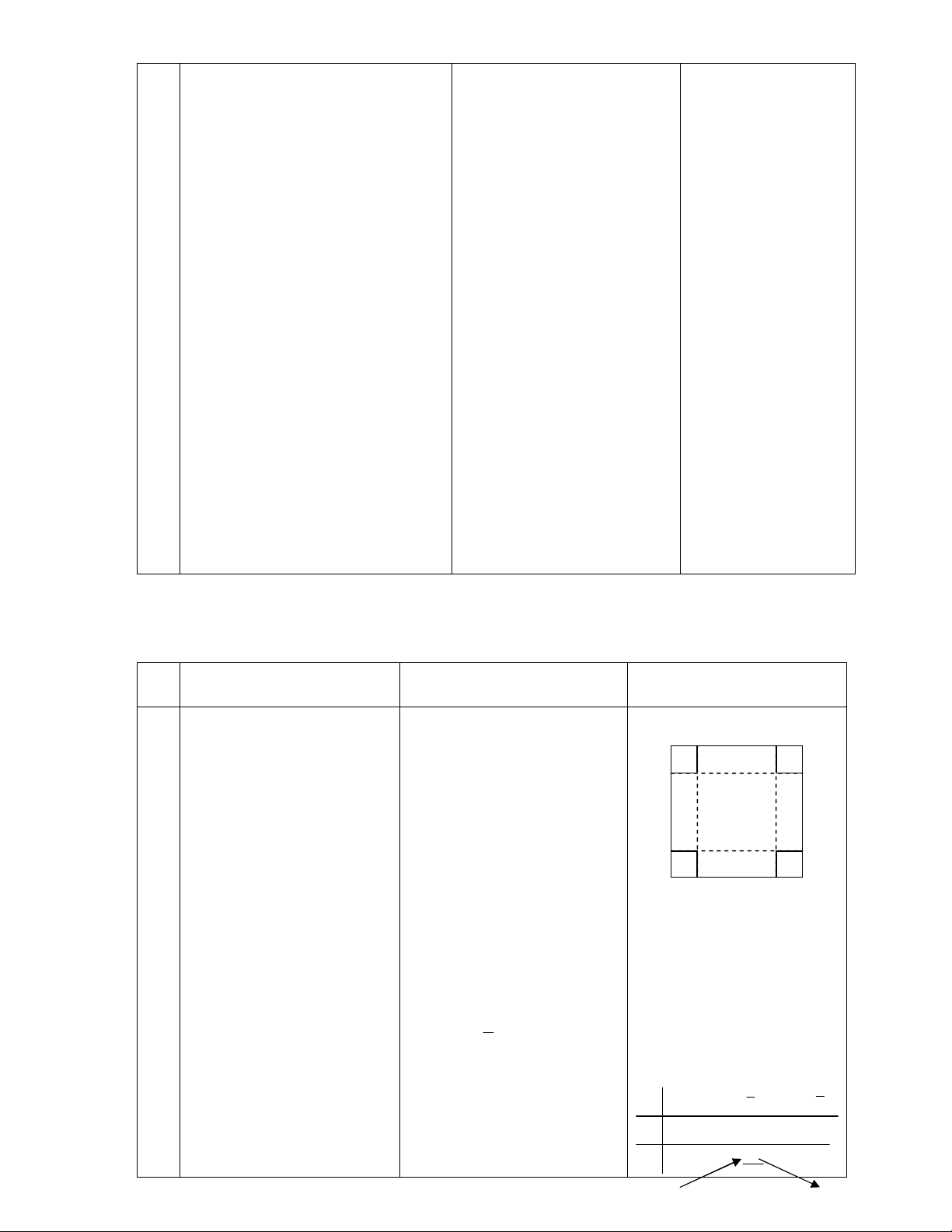
Có 1 tấm nhôm hình
vuông cạnh a. Cắt ở 4 góc
hình vuông 4 hình vuông
cạnh x. Rồi gập lại được 1
hình hộp chữ nhật không
có nắp.Tìm x để hộp này
có thể tích lớn nhất.
H: Nêu các kích thước của
hình hộp chữ nhật này?
Nêu điều kiện của x để
tồn tại hình hộp?
TL: các kích thướt là: a-2x;
a-2x; x
Đk tồn tại hình hộp là:
0
2
a
x
< <
V= x(a-2x)2
= 4x3 – 4ax2 + a2x
Bài toán:
Hướng dẫn hs trình bày
bảng
a x
x
V’
V
2
a
0
+ 0
-
3
2
27
a
6
a

H: Tính thể tích V của
hình hộp theo a; x.
H: Tìm x để V đạt max
Tính V’= 12x2 -8ax + a2
V’=0
6
2
a
x
a
x
é
=
ê
êÛ ê
=
ê
ë
Xét sự biến thiên trên
(
)
0;
2
a
Vmax=
3
2
27
a
khi
6
a
x
=
4/ Củng cố: (2’)
+ Nắm được k/n. Chú ý 0 0
/ ( )
x D f x M
$ Î =
+ Phương pháp tìm min, max trên tập D bằng cách dùng bbt của h/s
+ Nếu D=[a;b] thì có thể không dùng bảng biến thiên.
5/ Hướng dẫn học bài ở nhà:
+ Thuộc định nghĩa và nắm phương pháp tìm min, max
+ Bt 16 20. Bài tập phần luyện tập trang 23, 24 SGK.
Trường THPT Sào Nam
Số tiết 2 LUYỆN TẬP §2, §3
I/ Mục tiêu:


























