Trang 1
VẤN ĐỀ 1: KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
I. ỨNG DỤNG ĐẠO HÀM KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ:
1. Sự biến thiên và cực trị của hàm số:
1.1. Sự biến thiên của hàm số:
Cho hàm số y = f(x) xác định và có đạo hàm trên khoảng K = (a; b).
i) Nếu f'(x) 0 x K thì y = f(x) đồng biến (tăng) trên K.
ii) Nếu f'(x) 0 x K thì y = f(x) nghịch biến (giảm) trên K.
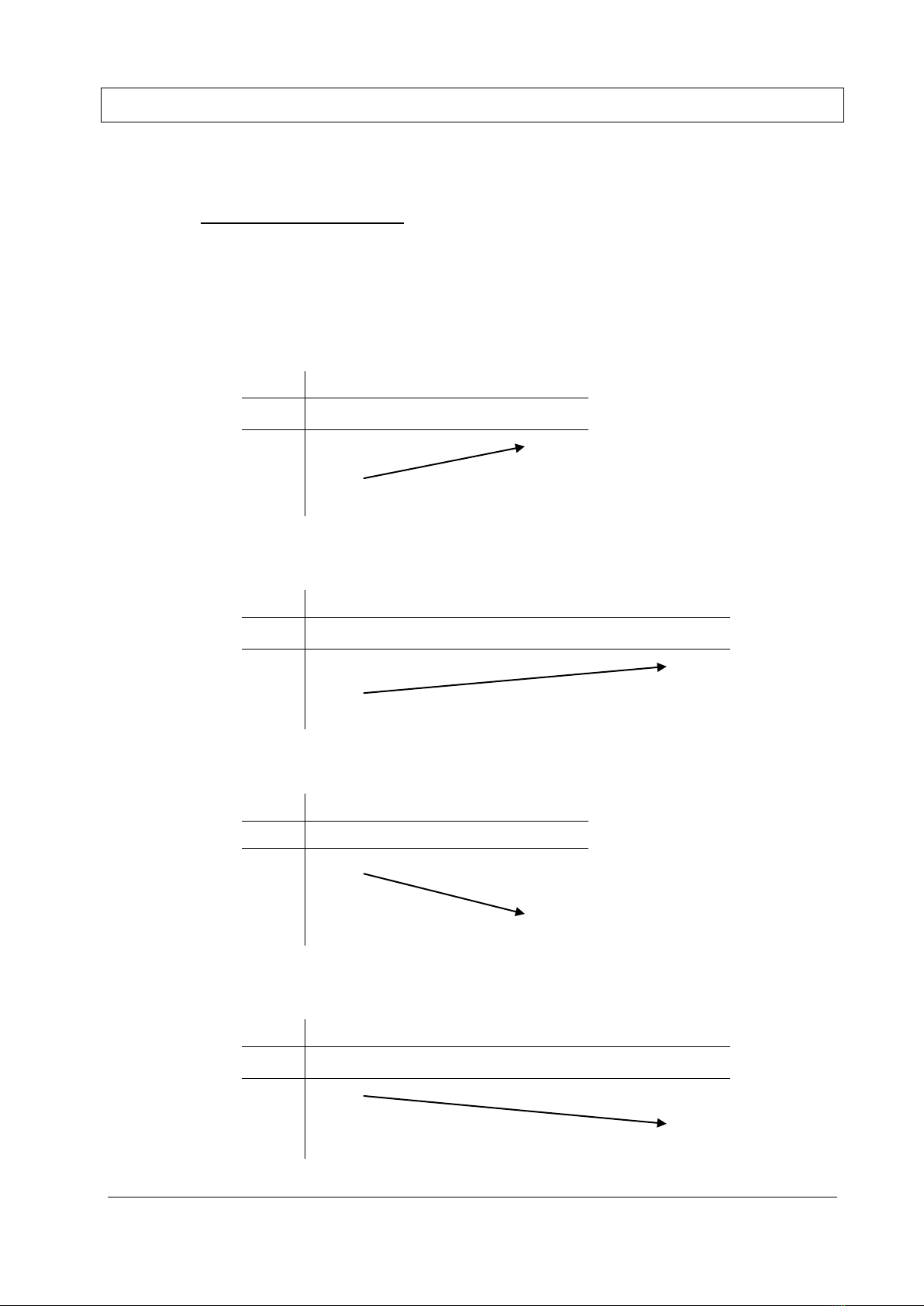
Bảng biến thiên:
i) y' > 0, x (a; b)
x
a
b
y'
+
y
ax
ylim
bx
ylim
Hàm số đồng biến (tăng) trên khoảng (a; b)
ii) y' 0, x (a; b) và y' = 0 tại một số hữu hạn điểm x0, x1, ..., xn
x
a
x0 x1 ..... xn
y'
+
+ 0 + 0 + 0 +
y
ax
ylim
bx
ylim
Hàm số đồng biến (tăng) trên khoảng (a; b)
iii) y' < 0, x (a; b)
x
a
b
y'
-
y
ax
ylim
bx
ylim
Hàm số nghịch biến (giảm) trên khoảng (a; b).
iv) y' 0, x (a; b) và y' = 0 tại một số hữu hạn điểm x0, x1, ..., xn
x
a
x0 x1 ..... xn
y'
-
- 0 - 0 - 0 -
y
ax
ylim
bx
ylim
Hàm số nghịch biến (giảm) trên khoảng (a; b).
Trang 2
1.2. Cực trị:
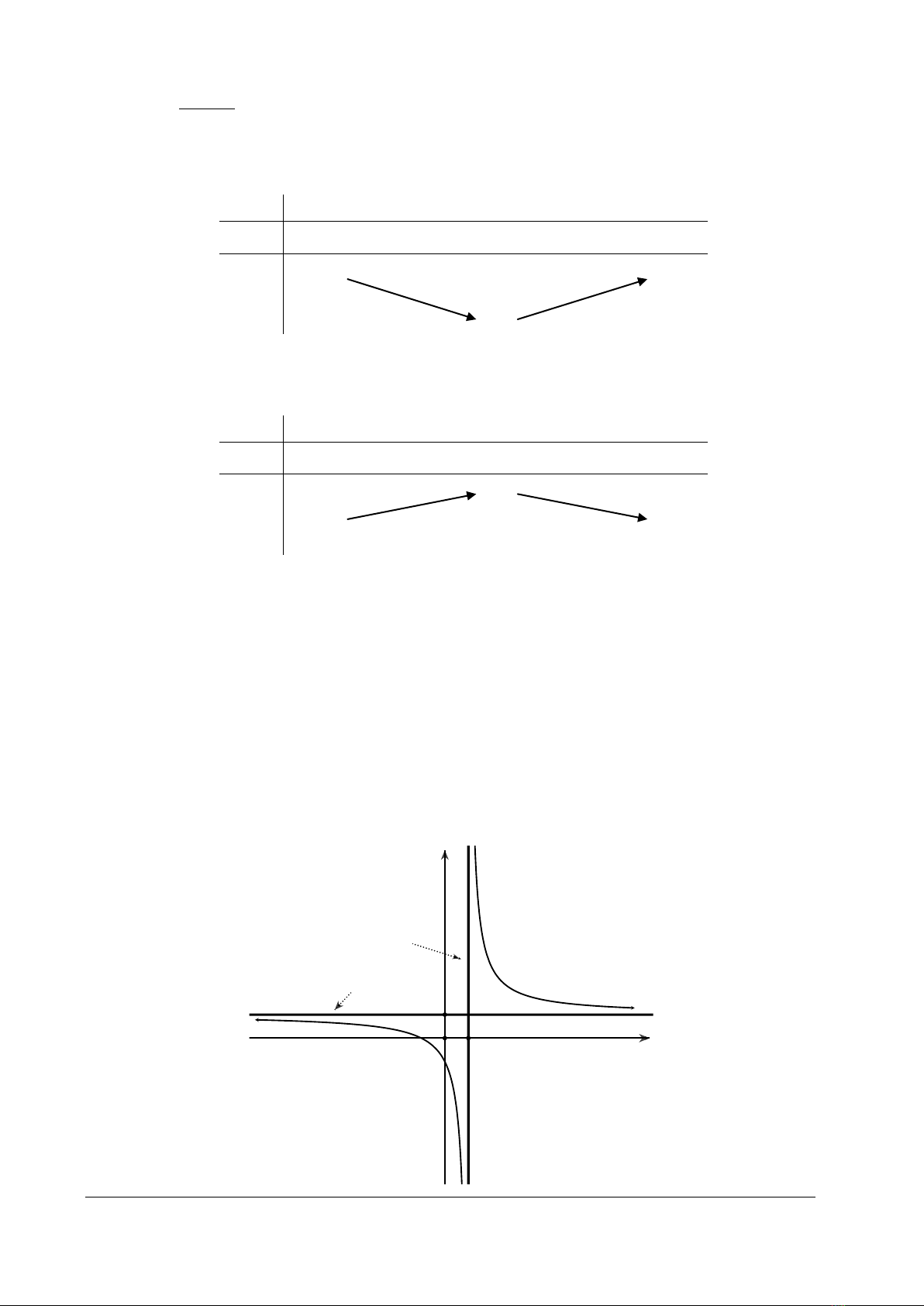
a) Dấu hiệu I:
Cho hàm số y = f(x) xác định và có đạo hàm trên khoảng (a; b)
i) Đạo hàm đổi dấu từ (-) sang (+) khi đi qua x0
x
a
x0
b
y'
-
0
+
y
ax
ylim
yCT
bx
ylim
Hàm số đạt cực tiểu tại x0 và yCT = f(x0).
ii) Đạo hàm đổi dấu từ (+) sang (-) khi đi qua x0
x
a
x0
b
y'
+
0
-
y
ax
ylim
yCĐ
bx
ylim
Hàm số đạt cực đại tại x0 và yCĐ = f(x0).
b) Dấu hiệu II:
Cho hàm số số y = f(x) xác định và có đạo hàm đến cấp 2 trên (a; b)
i) Nếu
0)(''
0)('
0
0
xf
xf
thì hàm số y = f(x) đạt cực đại tại x0.
ii) Nếu
0)(''
0)('
0
0
xf
xf
thì hàm số y = f(x) đạt cực tiểu tại x0.
* Chú ý: Nếu f''(x0) = 0 thì ta dùng dấu hiệu I để xác định điểm cực trị.
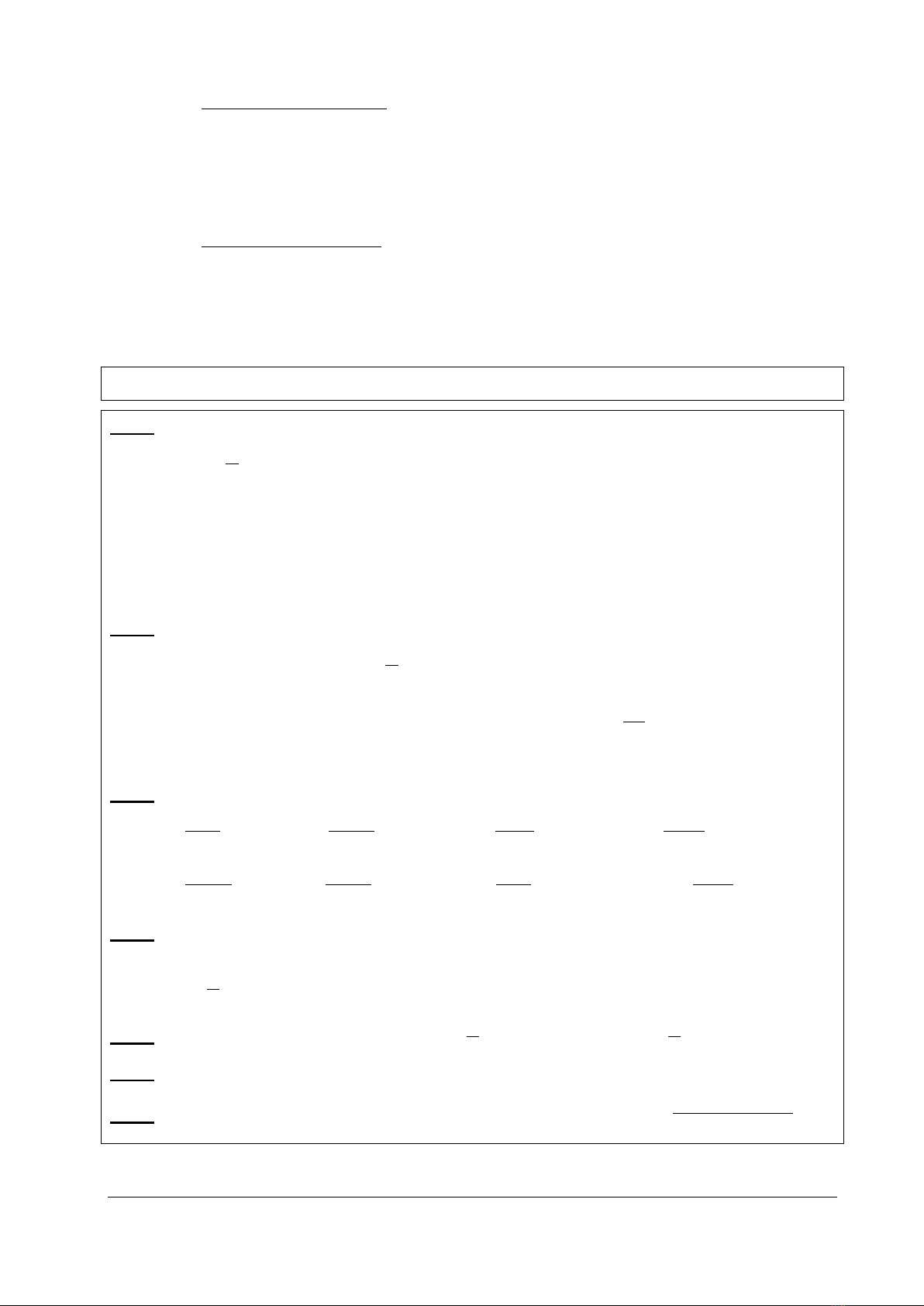
2. Đường tiệm cận của đồ thị hàm số:
Đường tiệm cận ngang
Đường tiệm cận đứng
x
y
O
Trang 3
2.1. Đường tiệm cận ngang: Cho hàm số y = f(x) xác định trên một khoảng vô hạn
(là khoảng dạng (a; +), (-; b) hoặc (-; +)). Đường thẳng y = y0 là đường tiệm cận
ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều
kiện sau được thỏa mãn:
f(x) = y0 (hoặc f(x) = y0).
2.1. Đường tiệm cận đứng: Đường thẳng x = x0 được gọi là đường tiệm cận đứng
(hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau
được thỏa mãn:
0
lim
xx
f(x) = + (hoặc
0
lim
xx
f(x) = - hoặc
0
lim
xx
f(x) = - hoặc
0
lim
xx
f(x) = +)
BÀI TẬP
Bài 1: Tìm các khoảng đơn điệu và cực trị của của mỗi hàm số sau:
a) y = x3 –
2
1
x2 - 2x + 2; b) y = x3 + 3x2 + 3x – 5;
c) y = x3 – 3x; d) y = x3– 3x + 2;
e) y = –x3 + 6x2 – 9x + 4; f) y = –x3 + 3x2;
g) y = x3– 3x2 + 3x – 2; h) y = x3 – 1;
i) y = x3 + x – 1; j) y = -x3 - x + 2;
k) y = –x3 – 3x2 – 4x + 2; l) y = –x3 + 3x2 – 5x + 2.
Bài 2: Xét sự đồng biến, nghịch biến và tìm cực trị của các hàm số sau:
a) y = x4 - 2x2; b) y =
2
1
x4 – 2x2 + 1; c) y = x4 - 4x2 + 1;
d) y = -x4 + 2x2; e) y = –2x4 + 4x2 + 2; f) y =
4
4
x
+ 2x2 + 1;
g) y = x4 + x2 - 2; h) y = x4 - 2x2 + 2; i) y = x4 – 2x2 + 3.
Bài 3: Khảo sát sự biến thiên và tìm tiệm cận của đồ thị các hàm số sau đây:
a) y =
1
1
x
x
; b) y =
1
12
x
x
; c) y =
3
1
x
x
; d) y =
x
x
2
2
;
e) y =
12
2
x
x
; f) y =
1
12
x
x
; g) y =
1
1
x
x
; h) y =
2
1
1
x
.
Bài 4: Áp dụng dấu hiệu 2 để tìm các điểm cực trị của các hàm số sau:
a) y = x4 - 2x2 + 1; b) y = sin2x - x; c) y = x5 - x3 - 2x + 1;
d) f(x) =
4
1
x4 - 2x2 + 6; e) f(x) = sin2x; f) y = sinx + cosx.
Bài 5: Xác định m để hàm số y = f(x) = x3 -
2
3
m2x2 + m có cực trị là
2
1
tại x = 1.
Bài 6: Với giá trị m nào thì y = -(m2 + 5m)x3 + 6mx2 + 6x - 5 đạt cực đại tại x = 1.
Bài 7: Tìm các giá trị của m để x = 1 là điểm cực tiểu của hàm số y =
1
1
2
x
mmxx
.
x
lim
x
lim
Trang 4
3. Khảo sát và vẽ đồ thị hàm số:
3.1. Hàm số bậc ba: y = ax3 + bx2 + cx + d (a 0)
Tập xác định: D = R
y' = f'(x)
y' = 0: giải phương trình y’ = 0
Giới hạn: =
y
x
lim
=
Bảng biến thiên:
Vẽ bảng biến thiên.
Kết luận sự đồng biến, nghịch biến của hm số.
Kết luận các điểm cực trị của đồ thị hàm số.
Điểm đặc biệt:
Điểm uốn: I(x0; f(x0)) {với x0 là nghiệm phương trình y'' = 0).
Giao điểm với trục Ox: x = 0 tìm y.
Giao điểm với trục Oy: y = 0 giải phương trình f(x) = 0 tìm x (nếu có).
Đồ thị: đồ thị hàm số nhận điểm uốn I làm tâm đối xứng.
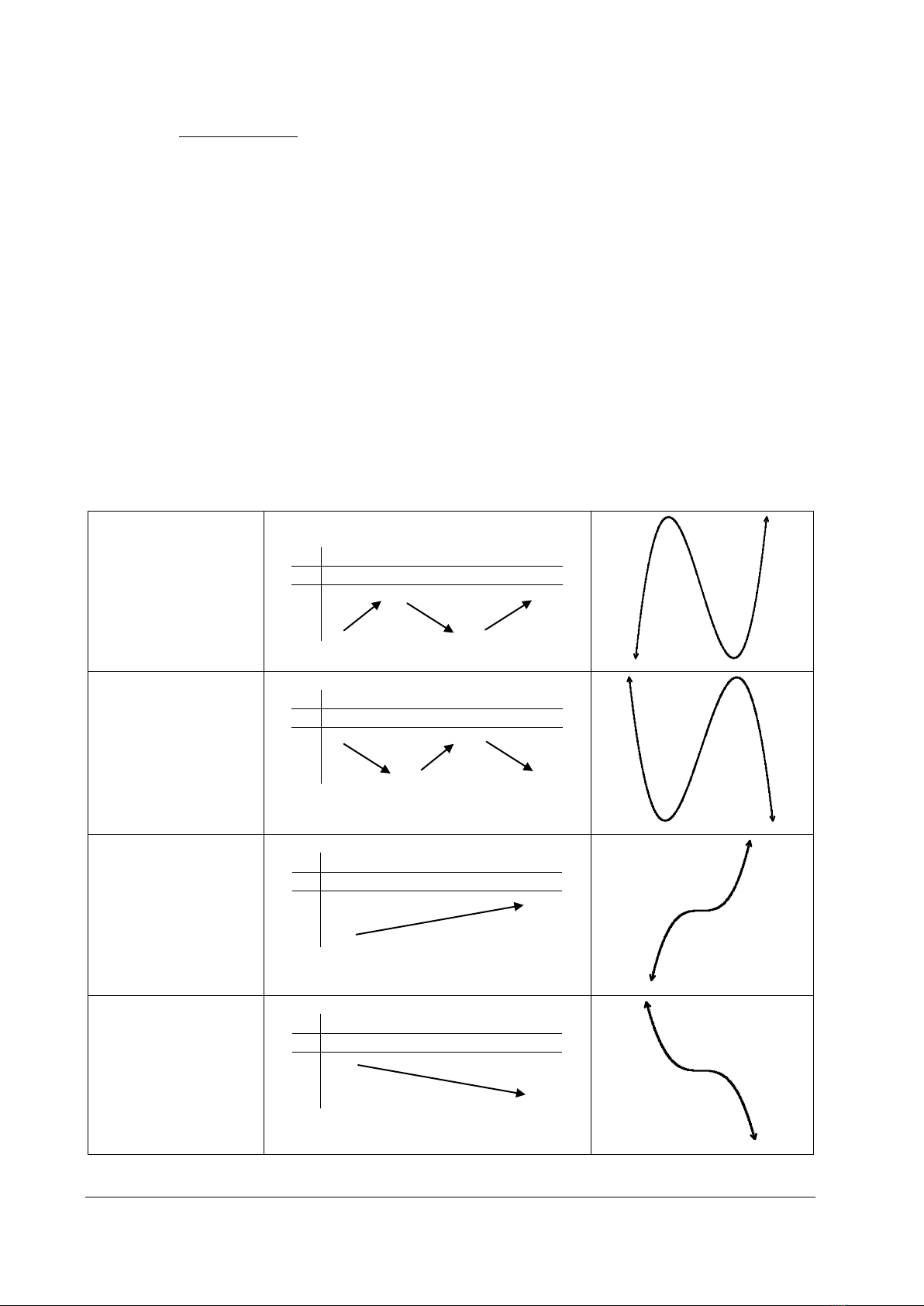
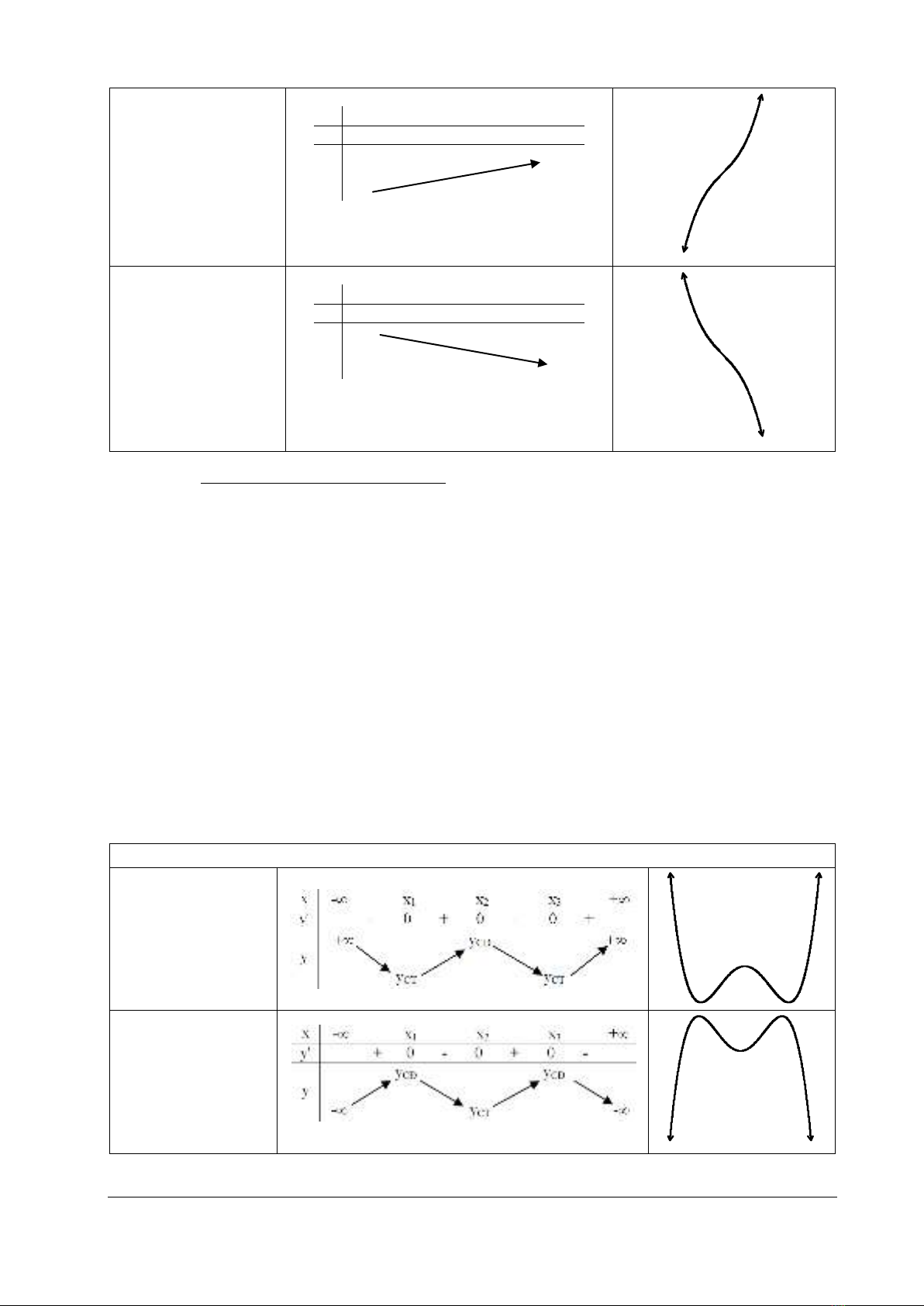
HÌNH DẠNG ĐỒ THỊ HÀM SỐ BẬC 3
0a
nghieäm2coù0'y
(x1, x2 là 2 nghiệm của
y'= 0)
x
- x1 x2 +
y'
+ 0 - 0 +
y
fCĐ +
- fCT
0a
nghieäm2coù0'y
(x1, x2 là 2 nghiệm của
y'= 0)
x
- x1 x2 +
y'
- 0 + 0 -
y
+ fCĐ
fCT -
0a
nghieämcoù10'y
(x0 là nghiệm của y'= 0)
x
- x0 +
y'
+ 0 +
y
+
-
0a
nghieämcoù10'y
(x0 là nghiệm của y'= 0)
x
- x0 +
y'
- 0 -
y
+
-
y
x
lim
Trang 5
0a
nghieämvoâ0'y
x
- +
y'
+
y
+
-
0a
nghieämvoâ0'y
x
- +
y'
-
y
+
-
3.2. Hàm số bậc bốn trùng phương: y = ax4 + bx2 + c (a 0)
Tập xác định: D = R
y' = f'(x)
y' = 0: giải phương trình y’ = 0
Giới hạn: = =
Bảng biến thiên.
Vẽ bảng biến thiên.
Kết luận sự đồng biến, nghịch biến của hm số.
Kết luận các điểm cực trị của đồ thị hàm số.
Điểm đặc biệt:
Giao điểm với trục Oy: x = 0 tìm y.
Giao điểm với trục Ox: y = 0 giải phương trình f(x) = 0 tìm x (nếu có).
{Lấy y = c giải phương trình ax4 + bx2 = 0 để tìm thêm điểm đặc biệt}
Đồ thị: đồ thị hàm số nhận trục tung làm trục đối xứng.
HÌNH DẠNG ĐỒ THỊ HÀM SỐ BẬC 4 TRÙNG PHƯƠNG
Hàm số y = ax4 + bx2 + c (a 0)
0a
nghieämcoù 30'y
(x1, x2, x3 là 3 nghiệm
của y'= 0)
0a
nghieämcoù 30'y
(x1, x2, x3 là 3 nghiệm
của y'= 0)
y
x
lim
y
x
lim